Задачи для самостоятельного решения
Вычислить следующие поверхностные интегралы второго рода:
130.
,
где
- положительная сторона куба, составленного
плоскостями
.
131.
,
где
- положительная сторона нижней половины
сферы
.
132.
,
где
- внешняя сторона эллипсоида
.
133.
,
где
- внешняя сторона пирамиды, составленной
плоскостями
.
Применяя
формулу Гаусса – Остроградского,
преобразовать следующие поверхностные
интегралы, если гладкая поверхность
ограничивает конечную область (тело) V
и
,
,
- направляющие косинусы внешней нормали
к:
134. . 135..
136.
.
137.
.
138.
,
где
- внешняя сторона поверхности, расположенной
в первом октанте и составленной из
параболоида
,
цилиндра
и
координатных плоскостей.
139. Вычислить интегралы 132, 133, применяя формулу Гаусса – Остроградского.
Ответы
1.
.
2.
.
3.
.
4. 1. 5. 1/ 40. 6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
14.
.
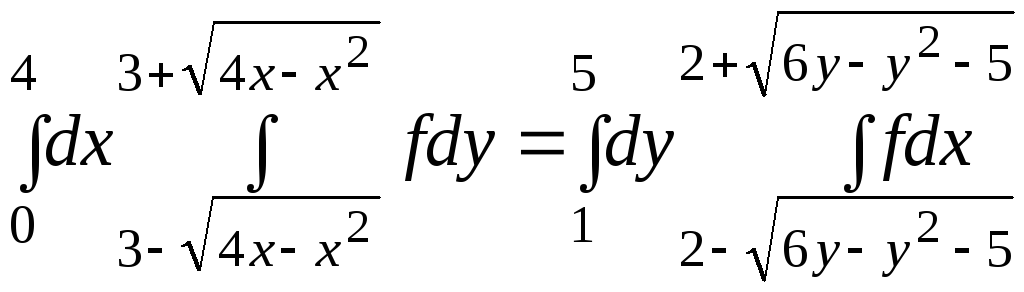15.
.
16.
.
17.
.
18.
.
19.
.
20. 0. 21. 33/140. 22. 9/4. 23. –2.
24.
.
25.
.
26.
.
27.
.
28.
.
29.
.
30.
.
31.
.
32.
.
33.
.
34.
.
35.
.
36.
.
37.
.
38.
.
39.
.
40.
.
41.
.
42.
.
43.
.
44.
а)
,
;
б)
.
45.
а)
;
б)
.
46.
а)
;
б)
.
47.
.
48.
.
49. 1/180. 50.
.
51.
.
52.
.
53.
.
54.
.
55.
или
,где
.
56.
.
57.
.
58.
.
59.
.
60.
.
61.
.
62.
.
63.560/3.
64.
.
65.
45.
66. 81/5.
67.
.
68. 27.
69.
.
70.
.
71.
и
.
72.
.
73.
.
74.
.
75.
.
76.
.
77.
.
78.
.
79.
.
80.
.
81.
.
82.24.
83.
.
84.
.
85.
.
86.
.
87.
.
88.
.
89.
.
90.
.
91.
.
92.
.
93.
.
94.
,
.
95.
.
96.
.
97.
.
98.
112/3.
99. 1/3.
100.
.
101.
.
102. 13.
103. 0.
104.
.
105.
4.
106.
.
107.0.
108. –9/2.
109.
.
110.
.
111.
.
112.
.
113.
.
114.
.
115.
.
116.
.
117.
1) 0;
2)
.
118. а)
;б) 0.
119.
.
120.
.
121.
.
122. 0. 123.
.
124.
.
125.
.
126.
.
127.
.
128.
.
129.
.
130.
3.
131.
.
132. 0. 133. 1/8. 134.
.
135. 0. 136.
.
137. 0. 138.
.
ГЛАВА 15
Злементы векторного анализа
15.1. Векторные поля. Интегральные и дифференциальные
характеристики векторных полей
15.1.1. Векторные линии. Дифференциальные уравнения
векторных линий поля
Определение 1.Векторным полем называется часть
пространства (или все пространство), в
каждой точкеMкоторого
задано какое-либо физическое явление,
характеризуемое векторной величиной
.
Если в пространстве
введена декартова прямоугольная система
координат, то задание вектор - функции
поля
сводится
к заданию трех скалярных функций:
.
(1.1)
Простейшими геометрическими характеристиками векторных полей являются векторные линии и векторные трубки.
Определение 2.
Векторными линиями поля
называются линии (кривые), в каждой точкеMкоторых направление
касательной совпадает с направлением
поля в этой точке.
Определение 3.Векторной трубкой называется поверхность, образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой, не совпадающей (хотя бы и частично) с какой – либо векторной линией.
Если поле задано формулой (1.1), то уравнение векторных линий дается системой дифференциальных уравнений
.
(1.2)
Замечание.Методы решения систем (1.2) (систем в симметрической форме) рассматриваются в теории дифференциальных уравнений.
Определение 4.Векторное поле
называется плоским, если в специально
подобранной системе координат оно имеет
вид:
(1.1)
Система уравнений (1.2) для таких полей имеет вид
(1.2)
и, таким образом, векторные линии плоского поля – это кривые, лежащие в плоскостях, параллельных плоскости Oxy.
Пример 1.Найти
векторные поля
(вектор
=const;
-
радиус вектор точки
).
Решение. Пусть
;
тогда
.
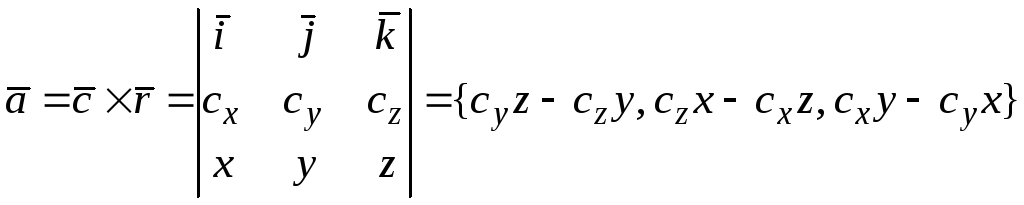Составим систему дифференциальных уравнений векторных линий (1.2):
.
Эту систему решаем методом интегрируемых комбинаций. Для получения интегрируемой комбинации умножим числитель и знаменатель первой дроби на x, второй – наy, третьей – наz; сложим почленно. По свойству пропорций получим
,
откуда получаем
интегрируемую комбинацию:
;
интегрируя ее, получим
- первый интеграл системы. Вторую
интегрируемую комбинацию получим,
умножая числитель и знаменатель первой
дроби на
,
второй – на
,
третьей – на
;
сложим почленно, получим
;
отсюда
и, следовательно,
.
Таким
образом система уравнений
определяет
искомые векторные линии: это окружности,
центры которых находятся на прямой,
проходящей через начало координат в
направлении вектора
;
плоскости, в которых они лежат,
перпендикулярны указанной прямой.
Пример 2. Найти векторные линии магнитного поля бесконечного проводника тока.
Решение.Считаем, что проводник направлен по осиOz, и в этом же направлении
течет ток
.
Вектор напряженности
магнитного поля, создаваемого током,
равен
,
где
- вектор тока,
- радиус вектор точки
;
- расстояние от оси проводника до точкиM. Имеем, далее,
,
и уравнение (1.2)
имеет вид:
,
,
откуда
-
векторные линии суть окружности с
центрами на осиOz.