Задачи для самостоятельного решения

Изобразить указанные ниже области и записать как правильные: а) в направленииOz, б) в направлении Ox.

44. Область V ограничена поверхностями .

45. Область V ограничена поверхностями .

46. Область V ограничена поверхностями .

14.3.2. Вычисление тройного интеграла в декартовых координатах

Пусть правильная в направлении Oz область V ограничена снизу и сверху непересекающимися поверхностями и, а с боков – цилиндрической поверхностьюF(x,y)=0 c образующими, параллельными оси Oz, т.е.

, где S- проекция V на плоскости Oxy.

Теорема 14.4. Пусть:1) в области задана функцияf(x,y,z), интегрируемая по Риману, т.е. существует тройной интеграл ; 2) существует повторный интеграл. Тогда справедлива формула

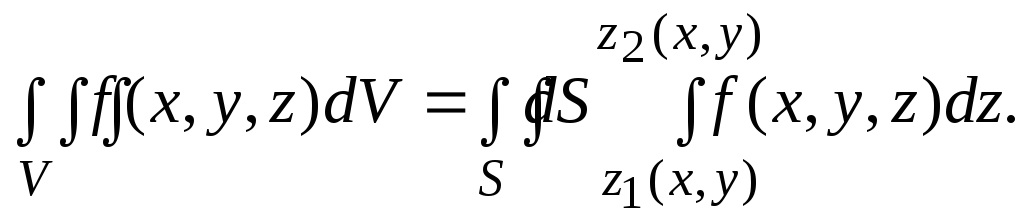(3.4)

Замечание. Цилиндрическая поверхность , ограничивающаяV, может частично или полностью вырождаться в пространственную линию.

Задания. Записать формулы, связывающие тройной интеграл с повторным, в случаях, когда: 1) область V правильная в направлении Ox проецируется на плоскость Oyz; 2) область V правильная в направлении Oy проецируется на плоскость Oxz.

Пример 11. Вычислить , где областьV ограничена

поверхностями: .

Поверхности иесть параболические цилиндры с образующими, параллельными- плоскости. ОбластьV – правильная в направле-

Рис.14.15

Рис.14.16

нии Oz, а потому для точек, принадлежащихV (рис.14.15).

Проекция V на плоскость Oxy есть правильная область S, ограниченная линиями и(рис.14.16), а потому, например (см.(2.1)),и в силу (3.2). Тогда по формуле (3.4)==

==см. (2.3)= ==

Задачи для самостоятельного решения

Вычислить интегралы:

47. .

48. , - область, ограниченная плоскостями ,

.

49. ,V – область, ограниченная гиперболическим параболоидом и плоскостями.

50. ,V – область, ограниченная цилиндром и плоскостямии.

51. ,V – область, ограниченная поверхностями .

14.3.3 Замена переменных в тройном интеграле

Пусть функции осуществляют взаимно однозначное непрерывно дифференцируемое отображение области из пространства Ouvw на область V пространства Oxyz. Тогда существует обратное непрерывно дифференцируемое отображение области V на область , если якобиан преобразования

.

Величины u,v,w можно рассматривать как прямоугольные координаты для точек области  и в то же время как криволинейные координаты точек области V. Точки пространства Oxyz , для которых одна из координат u, v, w сохраняет постоянное значение, образуют координатную поверхность. Всего будет три семейства таких поверхностей.

Теорема 14.5. Пусть , , есть диф-ференцируемое преобразование области  из пространства Ouvw в область V из пространства Oxyz. Тогда

. (3.5)

Замечание. Последнее равенство сохраняет справедливость, когда условие взаимно однозначного соответствия между областями V и  нарушается в отдельных точках или вдоль отдельных линий, или на отдельных поверхностях.

Переход в тройном интеграле к цилиндрическим координатам

Формулыпреобразуют цилиндрические координатыточкиM в декартовы координаты этой точки и переводят область изменения криволинейных координат (или) на все пространство Oxyz. Геометрически: - радиус-вектор OM точки P – проекции точки M на плоскость Oxy; - угол между Ox и OP; z- ап- Рис. 14.17. пликата точки M (рис. 14.17).

Обратное преобразование задается формулами:

Фиксируя в последних формулах , получим тройку координатных поверхностей: круговой цилиндр с осьюOz , полуплоскость, исходящую из оси Oz, и плоскость, параллельную плоскости Oxy (рис.14.17).

Я

Рис.14.17

кобиан преобразования

При переходе в тройном интеграле к цилиндрическим координатам формула (3.5) примет вид0

, (3.6)

где  - область изменения цилиндрических координат точек области V из Oxyz.

Переход к сферическим координатам

Формулы ,,преобразуют сферические координатыточкиM в декартовы координаты этой точки и переводят область (или ) изменения сферических координат на все пространство Oxyz.

Геометрически: r - радиус-ветор OM точки M; - угол между осью Ox и проекцией радиус-вектора r на плоскость Oxy; - угол между осью Oz и радиус-вектором r, отсчитываемый по ходу стрелки часов (рис.14.18). Обратное преобразование имеет вид

, ,

,

Фиксируя в последних формулах, получим тройку координатных поверхностей: сферу, полуплоскость, полуконус, соответственно (рис.14.18).Якобиан преобразования

.

Рис.14.18

При переходе в тройном интеграле к сферическим координатам справедлива формула:

, (3.7)

где  - область изменения сферических координат точек области V из Oxyz.

Пример 12. Вычислить тройной интеграл , где.

 Область V ограничена полусферой и полуконусом (рис.14.18). Для удобства вычисления тройного интеграла перейдем к сферическим координатам по формулам: , при этом . Неравенства, описывающиеV , преобразуются: а)

б) .

Так как нет ограничений на , то. В итоге, область интегрирования в сферических координатах есть(этот же результат можно было усмотреть из чертежа). Тогда по формуле (3.7)=повторный интеграл "расщепился" в произведение определенных интегралов =

=.

Пример 13. Вычислить тройной интеграл , гдеV ограничена полусферой , цилиндроми плоскостью.

 Тело V и проекция его на плоскость Oxy - круг радиусаR изображены на рис.14.19 и 14.20. Для вычисления I перейдем к цилиндрическим координатам по формулам. Поверхности, ограничивающиеV преобразуются: а) , б), в)z=a . Так как нет ограничений на координату , то(или.Область интегрирования в цилиндрических координатах есть.

Т

Рис.14.20

Рис.14.19

огда по формуле (3.6)= = === ==.