Глава 14

Кратные интегралы

14.1. Определение кратного интеграла

Определение двойного и тройного интеграла

Пусть : 1) в ограниченной замкнутой области “ объема”v(E) задана ограниченная функция ; 2)- разбиение областина подобластис объемамии диаметрами,- диаметр разбиения; 3) зафиксируем точки,; 4) построиминтегральную сумму

.

Определение. Конечный предел I интегральной суммы приназываетсяm- кратным интегралом от функции f по области E и обозначается

или . (1.1)

Таким образом, по определению,

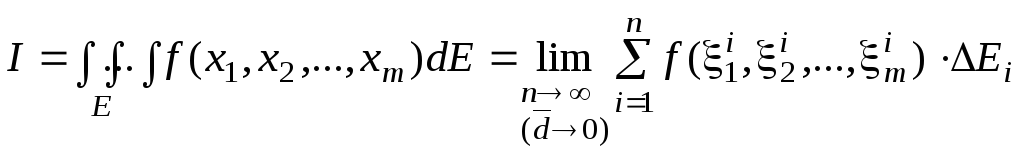(1.2)

В этом случае функция называетсяинтегрируемой в E.

При m=2 (m=3) для ограниченной функции f в замкнутой области ) кратный интеграл (1.1) называетсядвойным (тройным) интегралом, а соответствующее определение (1.2) примет вид

,где точка (,

где точка .

14.2. Двойные интегралы

14.2.1. Области на плоскости

Определение. Область назовемправильной в направлении Oy, если прямая, проходящая через любую внутреннюю точку из S параллельно оси Oy, пересекает границу области ровно в двух точках (рис.14.1).

Область S будет правильной в направлении Oy , если существуют функции и, определенные и непрерывные на [a;b] и такие, что координаты точек, принадлежащих (S), удовлетворяют условиям: ; тогда символически можно записать:

. (2.1)

Область S будет правильной в направлении Ox, если существуют функции и, определенные и непрерывные на [c;d] и такие, что координаты точек, принадлежащих S , удовлетворяют условиям: (рис.14.2);

тогда символически

. (2.2)

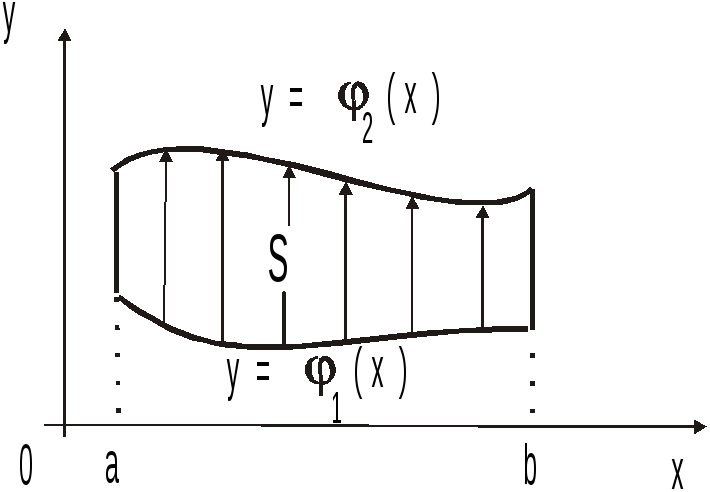
Рис.14.1. Рис.14.2.

Область называется правильной, если она правильная в обоих направлениях Ox и Oy.

Пример 1. Область S задана уравнениями границы: .

Изобразить указанную область и записать как правильную.



Рис.14.3

Область S – треугольник, ограниченный прямыми (рис.14.3). Точки пересечения прямых есть O(0;0), A(2;1), B(2;2). а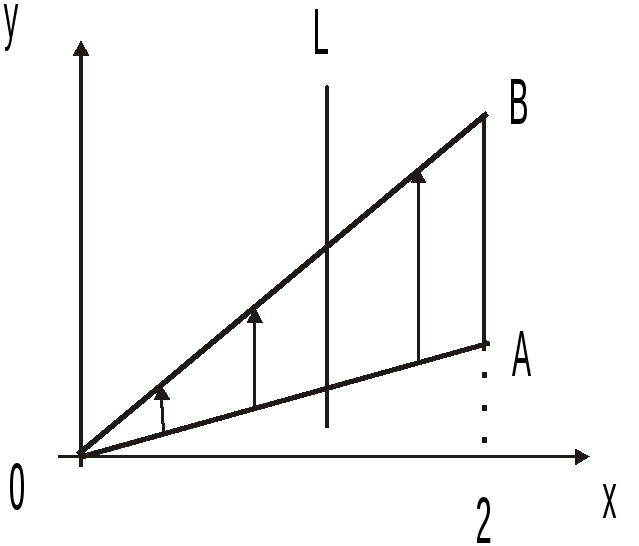) ОбластьS – правильная в направлении Oy и любая прямая L, проходящая через внутреннюю точку области, пересекает прямую и прямую. Поэтому в силу (2.1) область задается системой неравенств:.

б

Рис. 14.4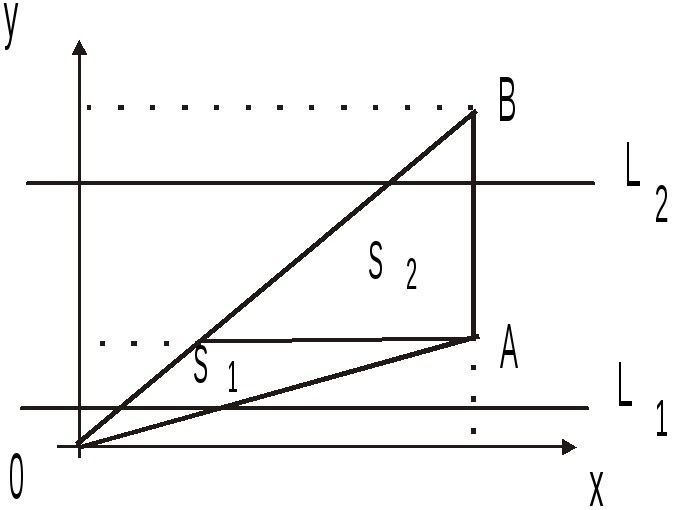

) Эта же область является правильной и в направленииOx, но для задания ее системой неравенств необходимо область S разбить на две части S₁ и S₂ (рис.14.4). Выразим в уравнениях границы x через независимую переменную y : OB: x=y, OA: x=2y. Для определения границ изменения переменной y проведем прямые, параллельные оси Ox. Прямая L₁ пересекает прямую OB: x=y и прямую OA: x=2y; прямая L₂ пересекает прямую OB: x=y и прямую AB: x=2. Итак, и в силу (2.2),.

Пример 2. Точки из области D удовлетворяют неравенству (a>0) , т.е. . Изобразить данную область и записать как правильную.

 Преобразуя неравенство , получим. Геометрически областьD есть круг радиуса a/2 c центром в точке С(a/2; 0). Из уравнения границы следуетили.ОбластьD может быть записана как правильная в направлении Oy (любая прямая, проходящая через внутреннюю точку D параллельно Oy, пересекает полуокружность и полуокружностьOML: (рис. 14.5)), в силу (2.1) .

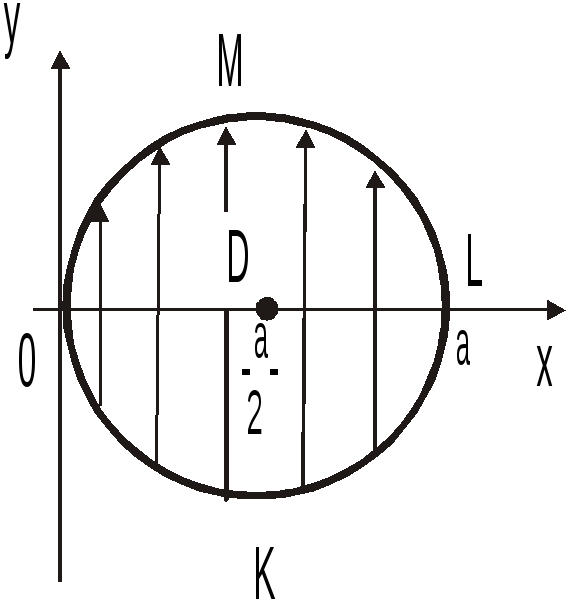
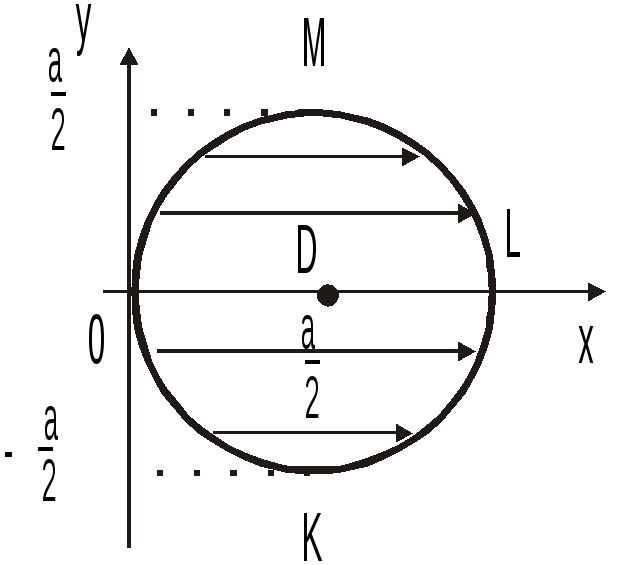Рис. 14.5 Рис.14.6

Область D можно записать как правильную в направлении Ox (прямая, проходящая через внутреннюю точку D параллельно Ox пересекает полуокружность

и полуокружность + (рис. 14.6)), и в силу (2.2): 