- •Глава 14
- •14.1. Определение кратного интеграла
- •14.2. Двойные интегралы
- •14.2.1. Области на плоскости
- •Задачи для самостоятельного решения
- •14.2.2. Повторный интеграл
- •Задачи для самостоятельного решения
- •14.2.3. Вычисление двойного интеграла в декартовых
- •Задачи для самостоятельного решения
- •8. . 9..
- •10. . 11..
- •14.2.4. Замена переменных в двойном интеграле.
- •Задачи для самостоятельного решения
- •14.3. Тройные интегралы.
- •Задания.
- •Задачи для самостоятельного решения
- •14.3.2. Вычисление тройного интеграла в декартовых координатах
- •Задачи для самостоятельного решения
- •14.3.3 Замена переменных в тройном интеграле
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •14.5.2 Криволинейные интегралы второго рода (ки-2)
- •105. . 106. . 107. .
- •14.6. Поверхностные интегралы
- •14.6.1. Двусторонние поверхности и их ориентация
- •14.6.2. Поверхностный интеграл первого рода (пи-1)
- •Задания
- •Задачи для самостоятельного решения
- •14.6.3. Поверхностные интегралы второго рода (пи-2)
- •Задачи для самостоятельного решения
- •134. . 135..
- •15.1.2. Поток векторного поля
- •1. Определение потока векторного поля
- •2. Способы вычисления потока
- •15.1.3. Линейный интеграл вектора. Циркуляция векторного поля
- •15.1.4. Дивергенция векторного поля
- •15.1.5. Ротор (вихрь) векторного поля
- •Задачи для самостоятельного решения
- •15.2.2. Соленоидальное векторное поле
- •15.2.3. Дифференциальные операции второго порядка.
- •Задачи для самостоятельного решения
- •124. 125. 126.
Задачи для самостоятельного решения
Перейти
в тройном интеграле
![]() к цилиндрическим координатам
к цилиндрическим координатам![]() или сферическим координатам
или сферическим координатам![]() и расставить пределы интегрирования:
и расставить пределы интегрирования:
52.
V
– область, находящаяся в первом октанте
и ограниченная поверхностями
![]() ,
,![]() .
.
53.
V
– область, ограниченная поверхностями
![]() .
.
54.
![]() .
.
55.
![]() .
.
Перейдя к цилиндрическим или сферическим координатам, вычислить интегралы:
56.
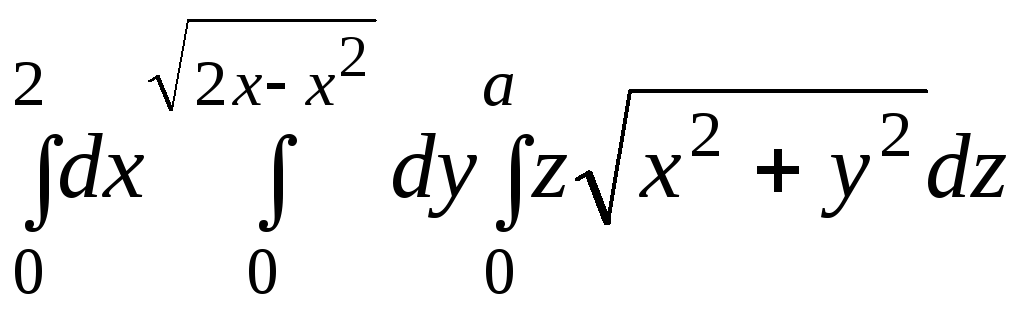 .
57.
.
57.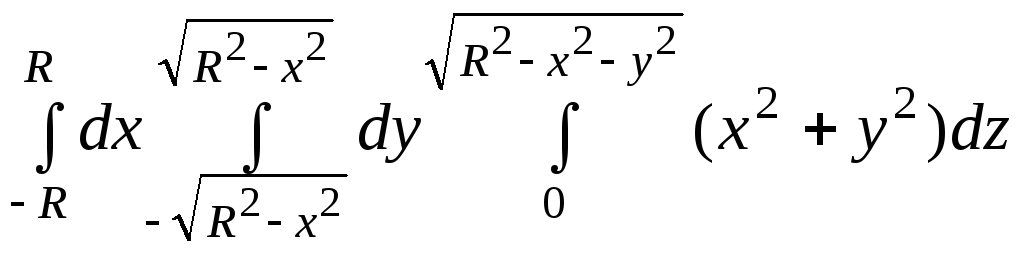 .
.
58.
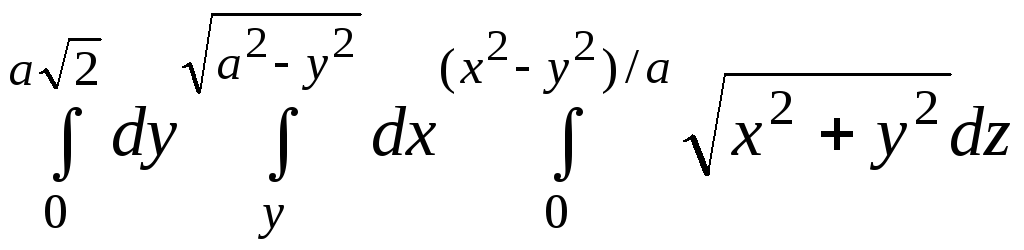 .
59.
.
59.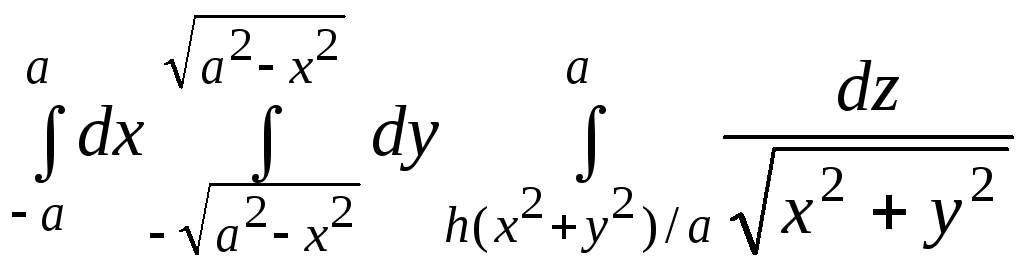 .
.
60.
![]() , где
, где![]() .
.
61.
![]() , где
, где![]() .
.
62.
![]() ,
где областьV
ограничена поверхностью
,
где областьV
ограничена поверхностью
![]() .
.
14.4. Некоторые приложения двойных и тройных интегралов
1.
Площадь
фигуры. а)
Для плоской фигуры
![]()
![]() .
(4.1)
.
(4.1)
б) Площадь части искривленной поверхности рассматривается в разделе 14.6. этой главы.
2.
Объем тела
V:
![]() (
(![]() -
проекцияV
на плоскость Oxy):
-
проекцияV
на плоскость Oxy):
![]() (4.2)
(4.2)
или
![]() . (4.3)
. (4.3)
3.
Масса. а)
Если
![]() - поверхностная плотность массы плоской
фигуры
- поверхностная плотность массы плоской
фигуры![]() ,
то
,
то
![]() .
(4.4)
.
(4.4)
б)
если
![]() -
объемная плотность массы тела
-
объемная плотность массы тела![]() ,
то
,
то
![]() .
(4.5)
.
(4.5)
Для
однородных фигур и тел плотность
![]() примем равной единице.
примем равной единице.
4.
Статические
моменты и координаты центра тяжести.
а) Для плоской
фигуры
![]() c
плотностью
c
плотностью
![]() и массойm
статические моменты относительно
координатных осей:
и массойm
статические моменты относительно
координатных осей:
![]() ,
,
![]() ;
;
координаты центра тяжести:
![]() ,
,
![]() .
.
б)
Для тела V
с плотностью
![]() и массойm
статические моменты относительно
координатных плоскостей
и массойm
статические моменты относительно
координатных плоскостей
![]() ,
,
![]() ,
,![]() ;
;
координаты центра тяжести:
![]() ,
,
![]() ,
,![]() .
.
Пример14.
Найти массу пластинки
![]() с поверхностной плотностью
с поверхностной плотностью![]() .
.
По
формуле (4.4)
![]() .
ОбластьD
и подынтегральная функция совпадают с
областью интегрирования и функцией из
примера 9 в пункте 14.2.4 при
.
ОбластьD
и подынтегральная функция совпадают с
областью интегрирования и функцией из
примера 9 в пункте 14.2.4 при
![]() ;
там же вычислен этот двойной интеграл,
поэтому
;
там же вычислен этот двойной интеграл,
поэтому![]() и при
и при![]() .
.
Пример
15. Найти
массу тела.
![]() ,
если объемная плотность
,
если объемная плотность![]() .
.
По
формуле (4.5)
![]() .
Тройной интегралI
по данной области V
вычислен в примере 12 из пункта 14.3.3,
.
Тройной интегралI
по данной области V
вычислен в примере 12 из пункта 14.3.3,
![]() ,
и потому
,
и потому![]() .
.
Пример
16. Найти
объем тела
![]()
![]()
![]() ;
;![]() ,
,![]() .
.
Из
формулы (4.3)
![]() . ТелоV
ограничено сферами, полуконусами и
плоскостями (рис.14.21).
. ТелоV
ограничено сферами, полуконусами и
плоскостями (рис.14.21).
|
a) |
|
Рис.14.21
Рис.14.21
в)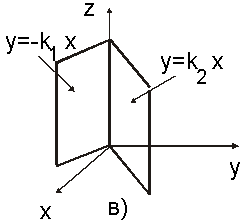
![]() по формулам:
по формулам:![]() ,
,![]() ,
,![]() .
Поверхности, ограничивающиеV,
преобразуются:1)
.
Поверхности, ограничивающиеV,
преобразуются:1)![]() ;
2)
;
2)
![]() ;
;
3)
![]() или
или
![]() ;
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() .
.
Область изменения сферических координат точек области V есть
![]() .
.
Тогда
в силу формулы (3.7)
![]() =
=
=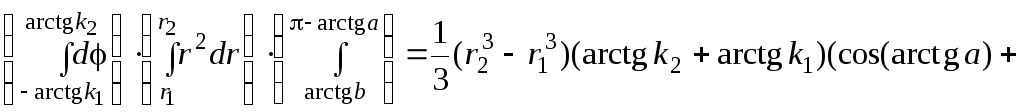
![]() .
.
Задачи для самостоятельного решения
Вычислить объемы тел, ограниченных заданными поверхностями:
63.
![]() .
64.
.
64.![]() .
.
65.
![]() .
.
66.
![]() .
67.
.
67.
![]()
68.
![]() -
гиперболический параболоид,
-
гиперболический параболоид,![]() .
.
69.
![]() .70.
.70.
![]() .
.
71.
![]() .72.
.72.
![]()
![]()
![]() .
.
73.
Найти массу квадратной пластинки со
стороной a
, если плотность пластинки в каждой
точке пропорциональна расстоянию этой
точки от одной из вершин и равен
![]() в центре квадрата.
в центре квадрата.
Найти координаты центра тяжести однородных пластинок, ограниченных кривыми:
74.
![]() .
75.
.
75.![]() .
.
76.
![]() .
77.
.
77.![]() - кардиоида,
- кардиоида,
![]() .
.
Найти координаты центра тяжести однородных тел, ограниченных поверхностями:
78.
![]() (усеченный
параллелепипед).
(усеченный
параллелепипед).
79.
![]() .
.
80.
![]() .
.
14.5. Криволинейные интегралы.
14.5.1. Криволинейные интегралы первого рода (КИ-1)
Пусть:
1) в точках простой (без точек
самопересечения), спрямляемой (т.е.
имеющей длину) кривой l
из пространства
![]() определена ограниченная скалярная
функция
определена ограниченная скалярная
функция![]() 2)
2)![]() -
произвольное разбиение кривойl
на элементарные дуги
-
произвольное разбиение кривойl
на элементарные дуги
![]() с длинами
с длинами![]() ;
3)
;
3)![]() -
произвольный набор точек; 4)
-
произвольный набор точек; 4)![]() -
интегральная сумма, соответствующая
данному разбиению кривой l
и выбору точек
-
интегральная сумма, соответствующая
данному разбиению кривой l
и выбору точек
![]() .
.
Определение.
Конечный предел интегральной суммы
![]() при
при![]()
![]() ,
не зависящий ни от способа разбиения
кривойl,
ни от выбора точек
,
не зависящий ни от способа разбиения
кривойl,
ни от выбора точек
![]() ,
называетсякриволинейным
интегралом первого рода
от функции
,
называетсякриволинейным
интегралом первого рода
от функции
![]() по кривойl:
по кривойl:
![]() .
.
Вычисление
КИ-1. Теорема 14.6.
Если кривая l
задана параметрическими
уравнениями:
![]() ,
где
,
где![]() - непрерывно дифференцируемые поt
функции и возрастание длины L
дуги кривой соответствует возрастанию
t,
то в предположении существования
определенного интеграла имеет место
равенство
- непрерывно дифференцируемые поt
функции и возрастание длины L
дуги кривой соответствует возрастанию
t,
то в предположении существования
определенного интеграла имеет место
равенство
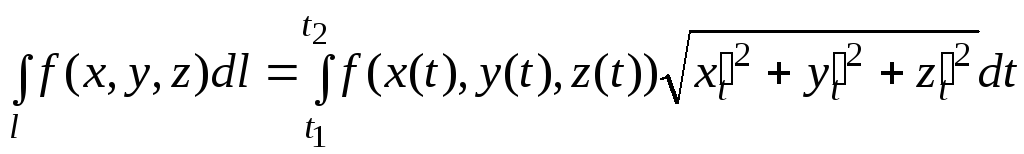 .
(5.1)
.
(5.1)
Следствия.
а)
Если плоская кривая l
задана явно:
![]() ,
и
,
и![]() ,
то
,
то
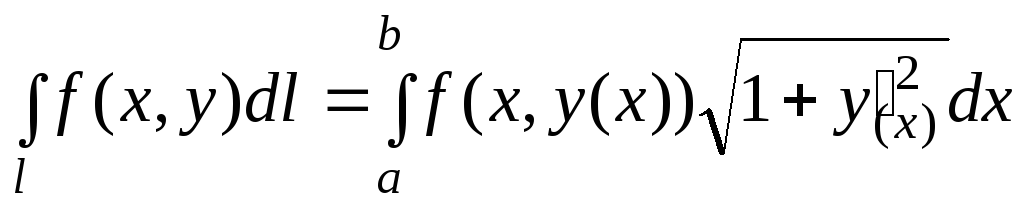 .
(5.2)
.
(5.2)
б)
Если плоская кривая l
задана в полярных
координатах:
![]() ,
то
,
то
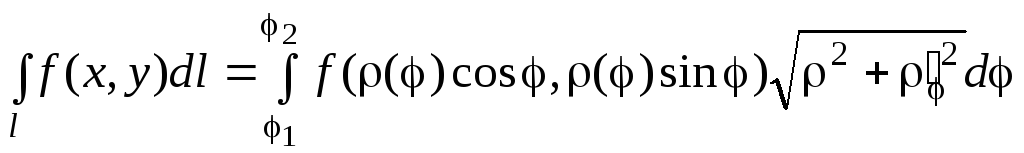 .
(5.3)
.
(5.3)
Некоторые приложения КИ-1
1.
Масса материальной линии. Пусть
![]() ,
,![]() -
линейная плотность массы материальной
линииl.
Тогда масса этой линии есть:
-
линейная плотность массы материальной
линииl.
Тогда масса этой линии есть:
![]() .
(5.4)
.
(5.4)
2.
Длина
пространственной (или плоской) кривой
l
есть L:
![]() .
.
3. Статические моменты и координаты центра тяжести.
а)
Для плоской
линии
![]() c
плотностью
c
плотностью
![]() и массойm
статические моменты относительно
координатных осей Oy
и Ox:
и массойm
статические моменты относительно
координатных осей Oy
и Ox:
![]() ,
,
![]() ;
;
координаты центра тяжести:
![]() ,
,
![]() .
.
б)
Для пространственной
линии l
c
плотностью
![]() и массойm
статические моменты относительно
плоскостей
и массойm
статические моменты относительно
плоскостей
![]() иOxy:
иOxy:
![]() ,
,
![]() ,
,
![]() ;
;
координаты центра тяжести:
![]() ,
,
![]() ,
,
![]() .
.
Пример
17. Вычислить
КИ-1:
![]() ,
гдеl
– прямолинейный отрезок, соединяющий
точки
,
гдеl
– прямолинейный отрезок, соединяющий
точки
![]() и
и![]() .
.
Уравнения
отрезка прямой AB
в параметрической форме:
![]() ,
,
![]() или
или
![]() .
Тогда
.
Тогда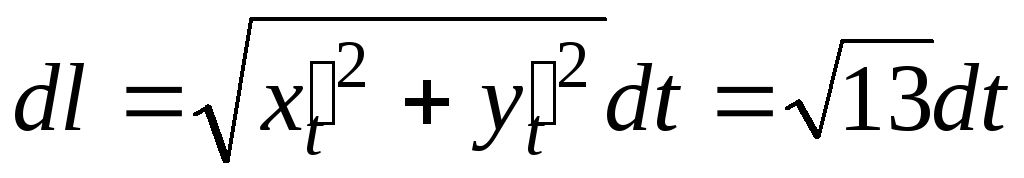 и из (5.1) имеем
и из (5.1) имеем![]()
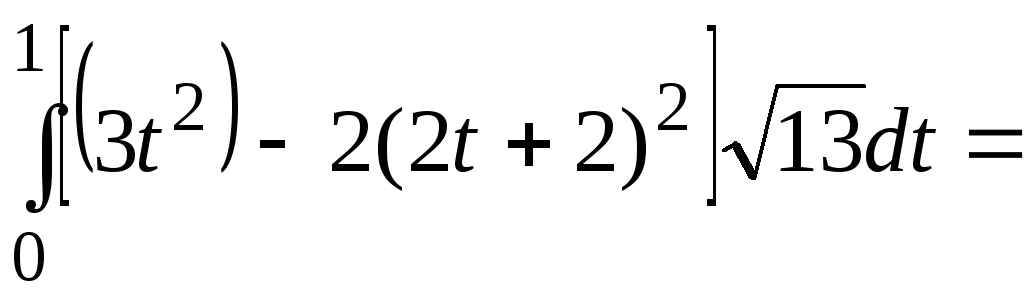
![]()
![]() .
.
Замечание.
В
случае явного задания отрезка прямой
![]()
![]() следует
воспользоваться формулой (5.2).
следует
воспользоваться формулой (5.2).
Пример
18.
Вычислить КИ-1:
![]() ,
гдеl
–
кривая, заданная уравнением
,
гдеl
–
кривая, заданная уравнением
![]() при условии
при условии![]() .
.
Для
построения кривой l
преобразуем уравнение ее к виду
![]() ;
таким образом,l
есть полуокружность с центром в точке
;
таким образом,l
есть полуокружность с центром в точке
![]() радиуса 1, расположенная слева от осиOy
(рис. 14.22).
радиуса 1, расположенная слева от осиOy
(рис. 14.22).
Н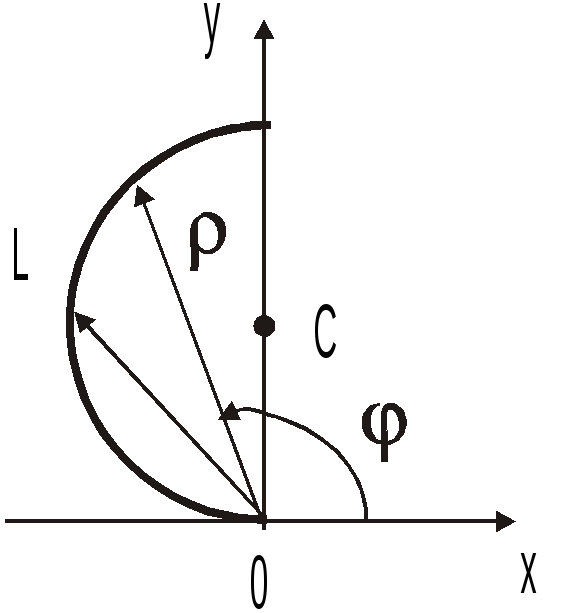 аличие
комбинации
аличие
комбинации![]() в подынтегральной функции и в уравненииl
наводит на мысль провести вычисления
в полярных координатах, которые связаны
с декартовыми координатами формулами
в подынтегральной функции и в уравненииl
наводит на мысль провести вычисления
в полярных координатах, которые связаны
с декартовыми координатами формулами
![]() .
Тогда: из
Рис. 14.22
.
Тогда: из
Рис. 14.22![]() получаем
получаем![]() – уравнениеl
в полярных координатах; из рис. 14.22 (или
условий
– уравнениеl
в полярных координатах; из рис. 14.22 (или
условий
![]() ,
,![]() ,
,![]() следует:
следует:![]() ;
;![]() ,
,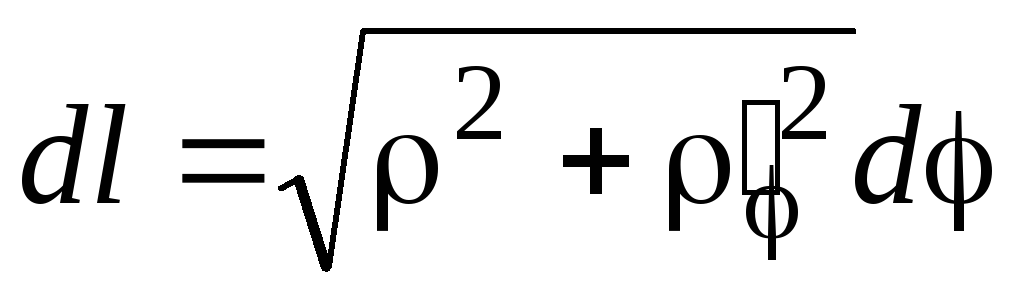 =
=
=
=![]() =
=![]() ,и из (5.3)
,и из (5.3)![]()
![]()
![]() .
.
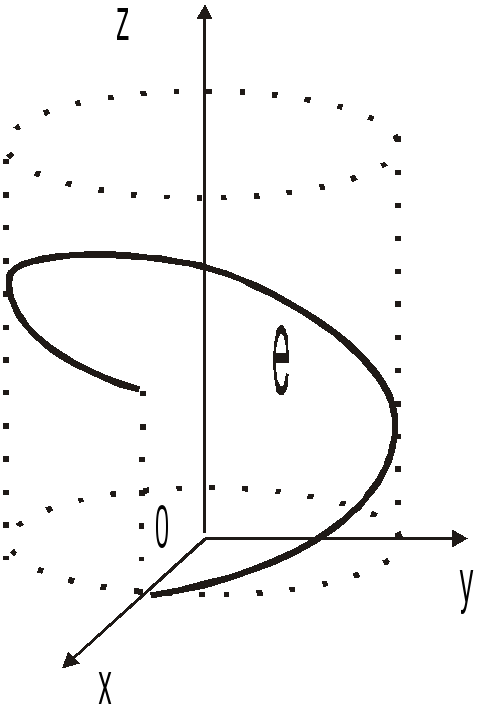
Пример
19.
Найти массу одного витка материальной
винтовой линии
![]() ,
,![]() ,
,![]() (рис. 14.23), если линейная плотность в
точке обратно пропорциональнаквадрату
расстояния этой точки от начала координат.
(рис. 14.23), если линейная плотность в
точке обратно пропорциональнаквадрату
расстояния этой точки от начала координат.
По
условию задачи плотность
![]() +
+
![]() =
=![]() ,
гдеk
– коэффициент про-
,
гдеk
– коэффициент про-
п
Рис.14.23. L
![]() .
Для одного витка
.
Для одного витка![]() . Из формул (5.4) и (5.1) имеем:
. Из формул (5.4) и (5.1) имеем:![]() =
=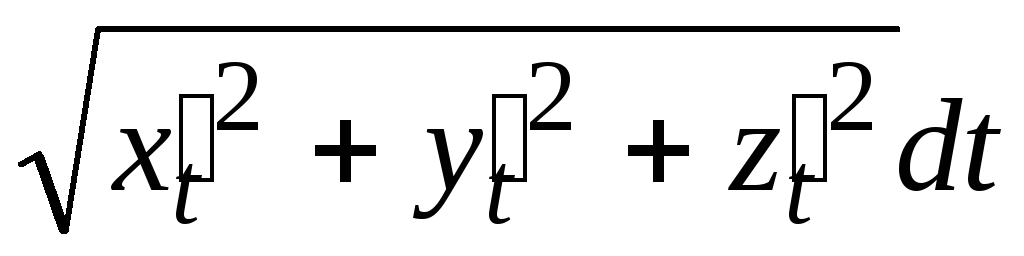
![]()
![]()
![]()
![]() =
=
![]() .
.