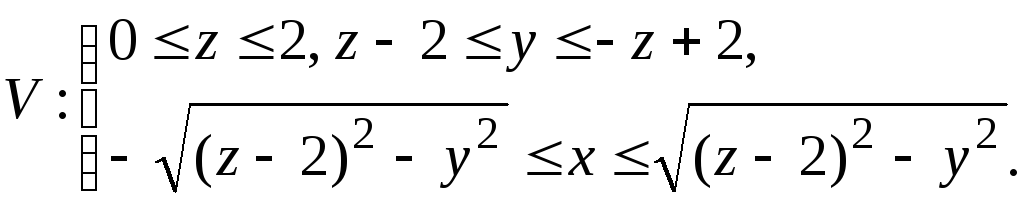- •Глава 14
- •14.1. Определение кратного интеграла
- •14.2. Двойные интегралы
- •14.2.1. Области на плоскости
- •Задачи для самостоятельного решения
- •14.2.2. Повторный интеграл
- •Задачи для самостоятельного решения
- •14.2.3. Вычисление двойного интеграла в декартовых
- •Задачи для самостоятельного решения
- •8. . 9..
- •10. . 11..
- •14.2.4. Замена переменных в двойном интеграле.
- •Задачи для самостоятельного решения
- •14.3. Тройные интегралы.
- •Задания.
- •Задачи для самостоятельного решения
- •14.3.2. Вычисление тройного интеграла в декартовых координатах
- •Задачи для самостоятельного решения
- •14.3.3 Замена переменных в тройном интеграле
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •14.5.2 Криволинейные интегралы второго рода (ки-2)
- •105. . 106. . 107. .
- •14.6. Поверхностные интегралы
- •14.6.1. Двусторонние поверхности и их ориентация
- •14.6.2. Поверхностный интеграл первого рода (пи-1)
- •Задания
- •Задачи для самостоятельного решения
- •14.6.3. Поверхностные интегралы второго рода (пи-2)
- •Задачи для самостоятельного решения
- •134. . 135..
- •15.1.2. Поток векторного поля
- •1. Определение потока векторного поля
- •2. Способы вычисления потока
- •15.1.3. Линейный интеграл вектора. Циркуляция векторного поля
- •15.1.4. Дивергенция векторного поля
- •15.1.5. Ротор (вихрь) векторного поля
- •Задачи для самостоятельного решения
- •15.2.2. Соленоидальное векторное поле
- •15.2.3. Дифференциальные операции второго порядка.
- •Задачи для самостоятельного решения
- •124. 125. 126.
Задачи для самостоятельного решения
Перейти
в двойном интеграле
![]() к полярным координатам
к полярным координатам![]() и расставить пределы интегрирования в
порядке: внешнее – по,
внутреннее - по :
и расставить пределы интегрирования в
порядке: внешнее – по,
внутреннее - по :
27.
D
– область, ограниченная окружностями
![]() ,
,![]() и прямыми
и прямыми
![]() ,
,
![]() .
.
28.
D
- область, являющаяся общей частью двух
кругов
![]() и
и![]() .
.
29.
D
- меньший из двух сегментов, на которые
прямая
![]() рассекает круг
рассекает круг![]() .
.
30.
D
- внутренняя часть правой петли лемнискаты
Бернулли
![]() .
.
31.
D:![]() .
.
32.
D:
![]() .Указание.
Перейти к эллиптическим полярным
координатам.
.Указание.
Перейти к эллиптическим полярным
координатам.
33.
D
- область, ограниченная линией
![]() .Указание.
Перейти к эллиптическим полярным
координатам.
.Указание.
Перейти к эллиптическим полярным
координатам.
34.
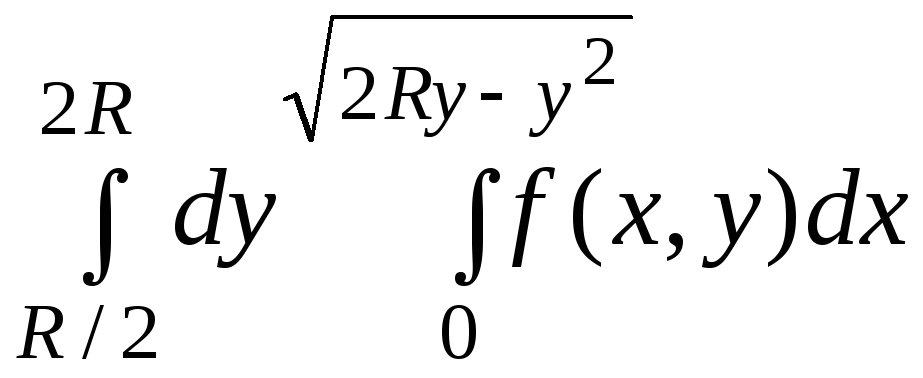 .
35.
.
35.
![]() .
36.
.
36.
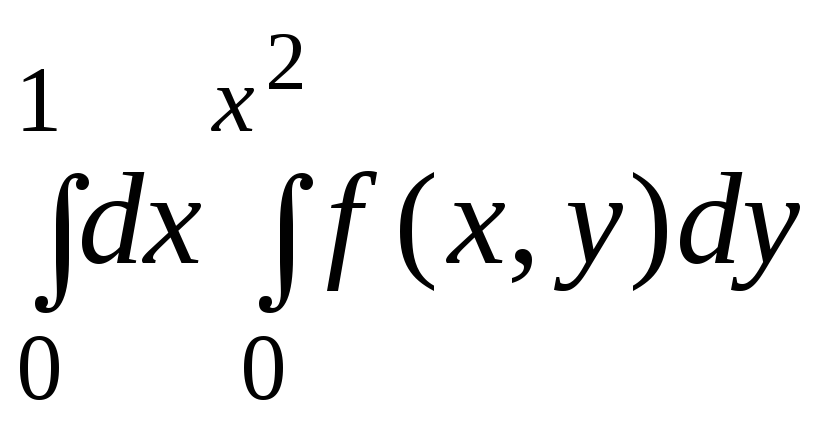 .
.
С помощью перехода к полярным координатам вычислить интегралы:
37.
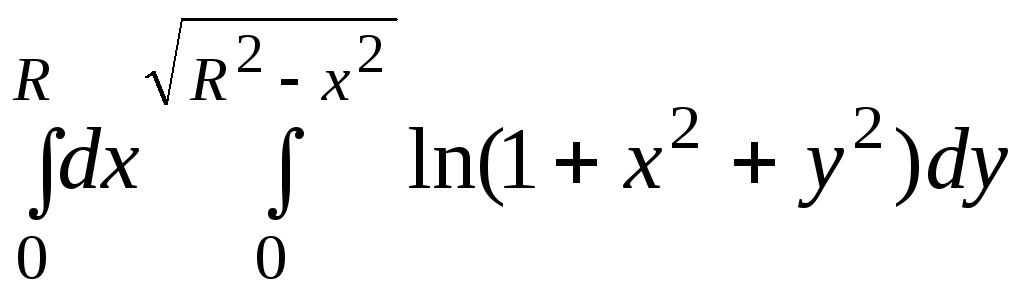 .38.
.38.
![]() .
.
39.
![]() .40.
.40.
![]() ,D
- часть кольца
,D
- часть кольца
![]() ,
,
![]() ,
,
![]() .41.
.41.
![]() .
.
Вычислить, перейдя к эллиптическим полярным координатам, интегралы:
42.
![]() .
.
43.
![]() -
область, ограниченная линией
-
область, ограниченная линией
![]() .
.
14.3. Тройные интегралы.
14.3.1. Области в пространстве.
Определение.
Область
![]() назовем правильной
в направлении
Oz
(правильной
в направлении Ox,
правильной
в направлении
Oy),
если прямая, проходящая через внутреннюю
точку области V
параллельно оси Oz
(параллельно оси Ox,
параллельно оси Oy)
пересекает границу области ровно в двух
точках.
назовем правильной
в направлении
Oz
(правильной
в направлении Ox,
правильной
в направлении
Oy),
если прямая, проходящая через внутреннюю
точку области V
параллельно оси Oz
(параллельно оси Ox,
параллельно оси Oy)
пересекает границу области ровно в двух
точках.
Область
V
будет правильной
в направлении
Oz,
если существуют функции
![]() и
и![]() ,
заданные вS
и такие, что координаты точек, принадлежащих
V,
удовлетворяют условиям:
,
заданные вS
и такие, что координаты точек, принадлежащих
V,
удовлетворяют условиям:
![]() .
Тогда символически записывают:
.
Тогда символически записывают:
![]() (3.1)
(3.1)
Если, в свою очередь, область S - правильная в направлении Oy, то (см.(2.1))
![]() .
(3.2)
.
(3.2)
Если область S правильная в направлении Ox, то (см.(2.2))
![]() .
(3.3)
.
(3.3)
Задания.
Записать символически правильную в направлении Oy область
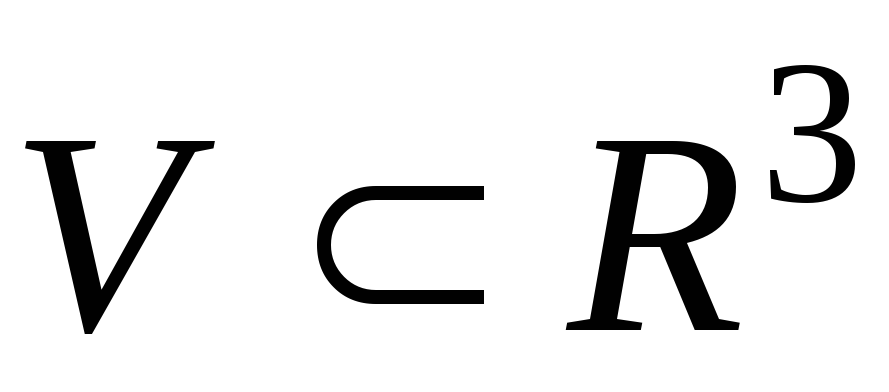 ,
если ее проекция на плоскостьOxz,
в свою очередь, есть правильная область.
,
если ее проекция на плоскостьOxz,
в свою очередь, есть правильная область.Записать символически правильную в направлении Ox область
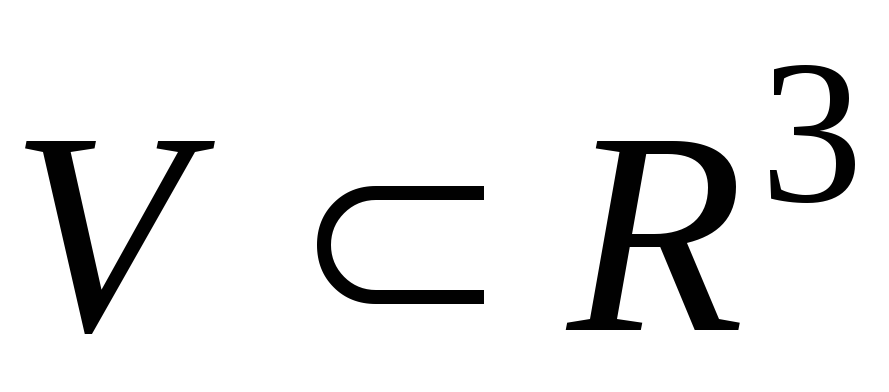 ,
если ее проекция на плоскостьOyz
есть
правильная область.
,
если ее проекция на плоскостьOyz
есть
правильная область.
Пример
10. Область
V
ограничена поверхностями
![]() и z=0.
Изобразить область и записать как
правильную: а) в направлении Oz,
и z=0.
Изобразить область и записать как
правильную: а) в направлении Oz,
б) в направлении Ox.
Рис.14.12 Рис.14.13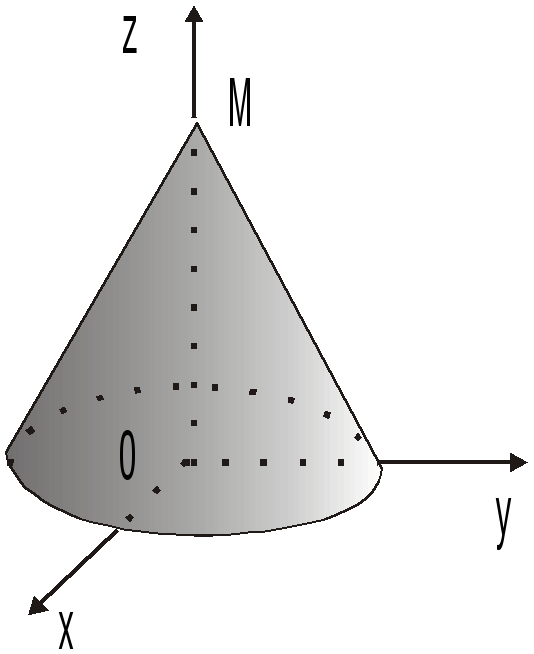
![]() ,
основанием, лежащим на плоскостиz=0,
с вершиной в точке M(0;0;2)
и осью, совпадающей с Oz
(рис. 14.12).Область V
- правильная во всех направлениях Ox,
Oy,
Oz.
При z=0
из уравнения
,
основанием, лежащим на плоскостиz=0,
с вершиной в точке M(0;0;2)
и осью, совпадающей с Oz
(рис. 14.12).Область V
- правильная во всех направлениях Ox,
Oy,
Oz.
При z=0
из уравнения
![]() имеем
имеем![]() -
уравнение окружности радиуса 2; таким
образом, в основании конуса круг. а)
Рассмотрим областьV
как правильную в направлении Oz.
Из уравнения
-
уравнение окружности радиуса 2; таким
образом, в основании конуса круг. а)
Рассмотрим областьV
как правильную в направлении Oz.
Из уравнения
![]() имеем
имеем
![]() .
Для точек областиV
имеем:
.
Для точек областиV
имеем:
![]() .
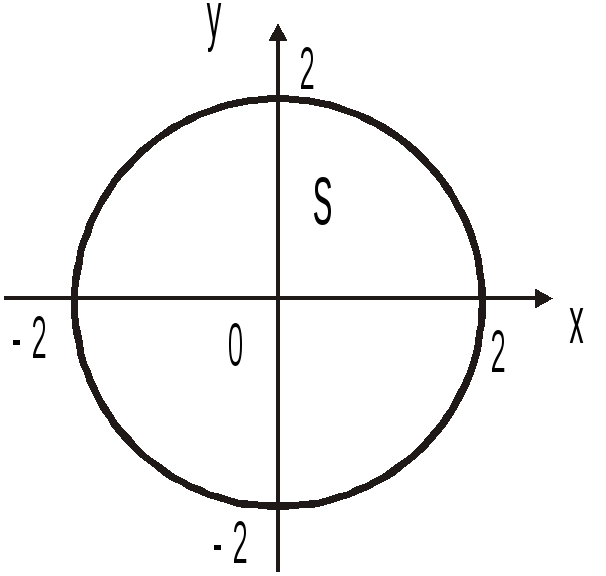
Проекция области V
на плоскость Oxy
есть
.
Проекция области V
на плоскость Oxy
есть
![]() (рис. 14.13), поэтому в силу (3.1)
(рис. 14.13), поэтому в силу (3.1)
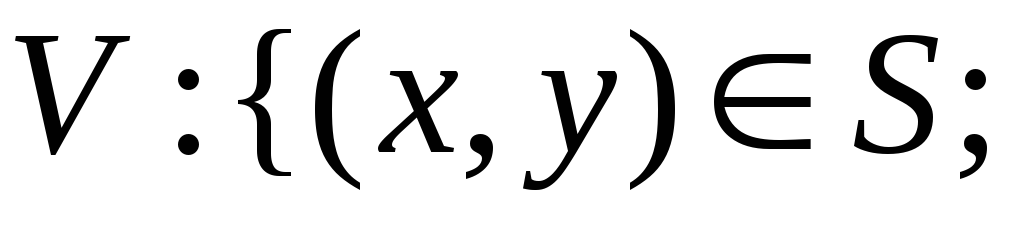
![]() ,где
,где
![]() .Так
как S
- правильная область, то (см.(2.1))
.Так
как S
- правильная область, то (см.(2.1))
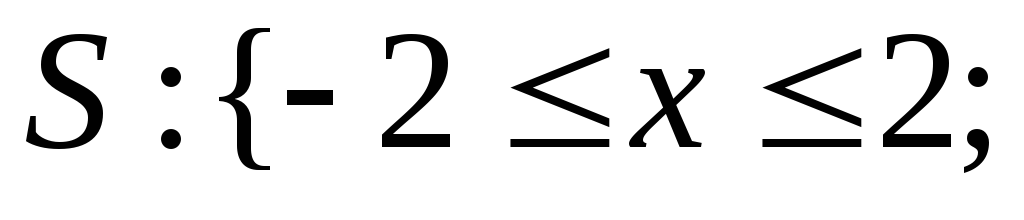
![]() или (см.(2.2))
или (см.(2.2))
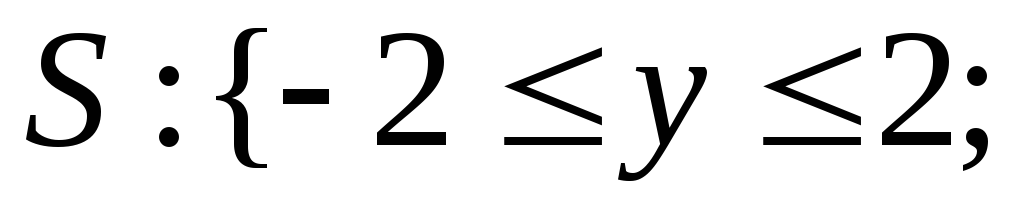
![]() .
Поэтому требуемая запись будет (см.
(3.2))
.
Поэтому требуемая запись будет (см.
(3.2))
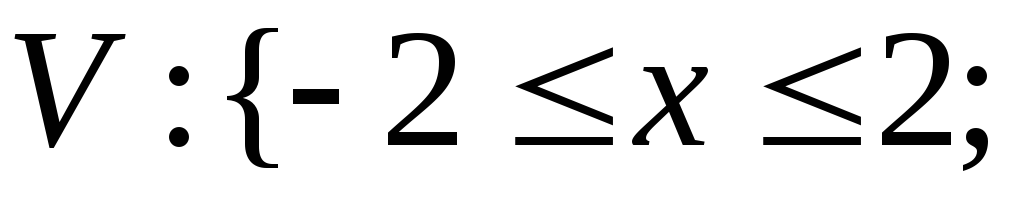
![]()
![]() или
(см. (3.3))
или
(см. (3.3))
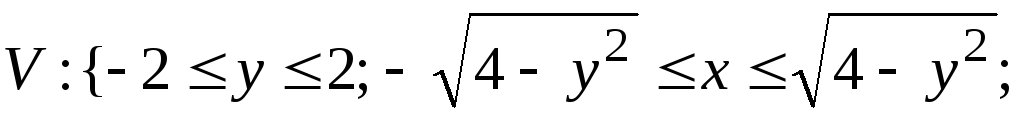
![]() .
.
б)
Рассматривая область V
как правильную в направлении Ox,
из уравнения
![]() имеем
имеем
![]() .
Линии пересечения плоскости Oyz
и конической поверхности находятся из
решения системы уравнений:
.
Линии пересечения плоскости Oyz
и конической поверхности находятся из
решения системы уравнений: ![]()
![]() ;
в результате имеем
;
в результате имеем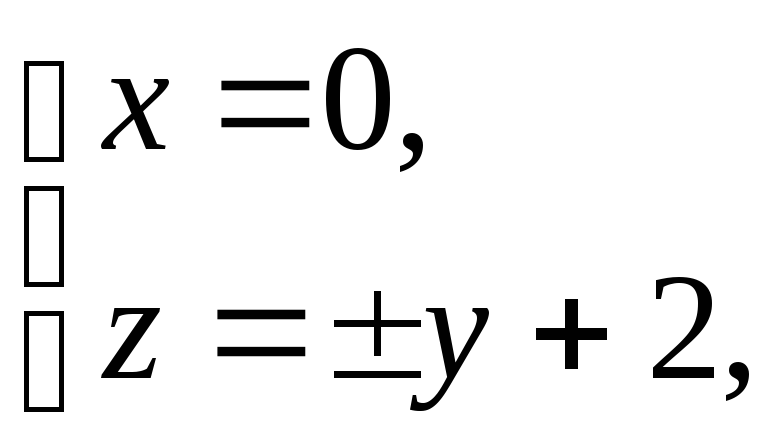 -
прямые в плоскостиOyz.
Итак, проекцией V
на плоскость Oyz
является область D
- треугольник со сторонами z=y+2,
z
= –y+2,
z=0
(рис. 14.14), поэтому в силу (3.1)
-
прямые в плоскостиOyz.
Итак, проекцией V
на плоскость Oyz
является область D
- треугольник со сторонами z=y+2,
z
= –y+2,
z=0
(рис. 14.14), поэтому в силу (3.1)
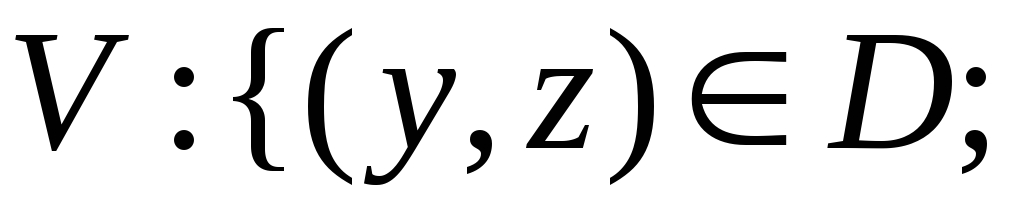
![]() ,
где
,
где
![]() .
.
2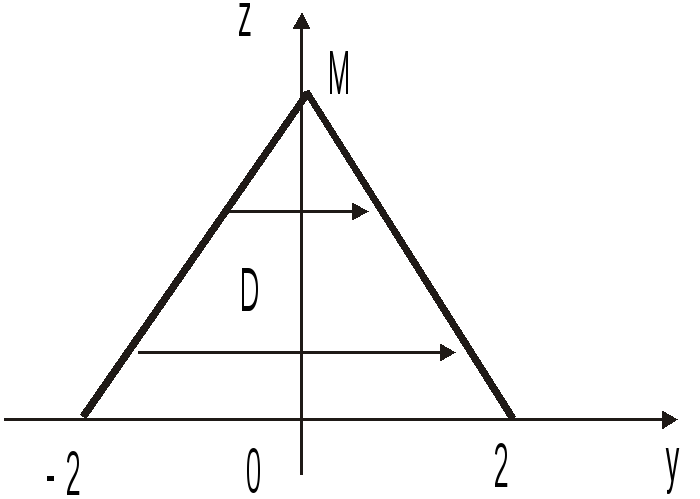
![]() ,
а потому
,
а потому
Рис.14.14