Задачи для самостоятельного решения

Изобразить указанные области и записать как правильные в направлении Oy.

1. S – параллелограмм со сторонами x=3, x=5, 3x-2y+4=0, 3x-2y+1=0.

2. Область D задана неравенствами .

3. Область D – треугольник со сторонами .

14.2.2. Повторный интеграл

Определение. Повторный интеграл есть приращение первообразнойF(x,y) дляпо переменному “y”, проинтегрированное по переменному “x” , т.е.

.

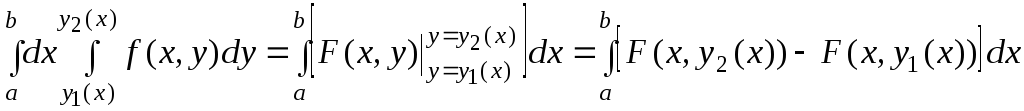Определение. Повторный интеграл есть приращение первообразнойФ(x,y) для f(x,y) по переменному “x”, проинтегрированное по переменному “y”, т.е.

=.

Пример 3. Вычислить повторный интеграл .

 интегрируя внутренний интеграл по “y”, полагаем “x” постоянным=

= .

Задачи для самостоятельного решения

Вычислить повторные интегралы.

4. . 5.6.. 7., если .

14.2.3. Вычисление двойного интеграла в декартовых

координатах

Теорема 14.1 Если : 1) функция f(x,y) интегрируема в правильной в направлении Oy области S: , т.е. существует двойной интеграл, 2) существует повторный интеграл, то

(2.3)

Теорема 14.2. Если :1) функция f(x,y) интегрируема в правильной в направлении Ox области , т.е. существует двойной интеграл, 2) существует повторный интеграл, то

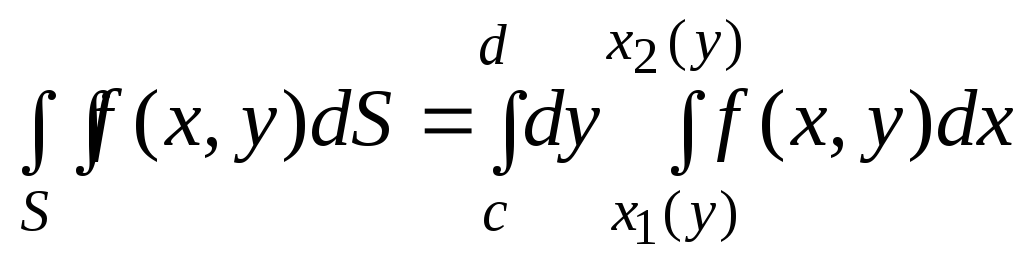. (2.4)

Из вышеприведенных теорем следует, что при вычислении повторного интеграла можно изменять порядок интегрирования.

Пример 4. Изменить порядок интегрирования в интеграле .



Рис.14.7

Так как из (2.4) имеем , то правильная в направленииOx область D ограничена линиями x=y, x=2-y, y=0, y=1 (линия y =1 выродилась в точку) (рис. 14.7). Эта область является правильной и в направлении Oy. Так как участок OAB границы состоит из отрезков прямых и, то, где (см. (2.1)),

. Итак, ===.

Пример 5. Вычислить по областиD, ограниченной линиями и.

Изобразим область D. Для отыскания точек пересечения парабол ирешаем уравнение , откуда имеем действительные корни,. Таким образом, параболы пересекаются в точках( рис. 14.8). РассматриваяD как правильную в направлении Oy (рис.14.8а), имеем (см.(2.1)) . По формуле (2.3)

Рис.14.8 а)

=.

Если областьD рассматривать как правильную в направлении Ox (рис.14.8б), то (см. (2.2)) . По формуле (2.4)

=

Рис.14.8.б

=. 

Задачи для самостоятельного решения

Изменить порядок интегрирования в следующих повторных интегралах:

8. . 9..

10. . 11..

Перейти от двойного интеграла по конечной областиD к повторному интегралу и расставить пределы интегрирования:

12. Область D – параллелограмм со сторонами .

13. .14. .

15. - треугольник со сторонами .

16. .

17. - треугольник с вершинами.

18. D – сегмент, ограниченный линиями .

Вычислить двойные интегралы:

19. . 20.-круг .

21. - область, ограниченная линиями.

22. - область, ограниченная линиями.

23. - область, ограниченная линиями.

24.- четверть круга , лежащая в первом квадранте.

25. - область, ограниченная параболойи прямой.

26. , еслиD ограничена осью абсцисс и первой аркой циклоиды ,,.