4. Похідна функції, геометричний і механічний сенс похідної. Таблиця похідної. Похідні складних функцій. Правила диференціювання. Диференціал функції. Рівняння дотичної до графіка функції.

Пусть функция определена в некоторой окрестности точки, эта функция имеет производную в точкеесли существует пределпри этом значение пределаназываетсяпроизводной функциейв точке.

приращение аргумента

приращение функции

Геометрический и механический смысл производной

Прямая является касательной к графику функциив точкеесли выполнено условие, т.е. еслиимеет вид:. Касательная к графику функцииyсуществует тогда и только тогда когда функцияyдифференцируема в точке. Касательной оказывается прямая, проходящая через точкус угловым коэффициентом.

. Коэффициент растяжения в точкеxравен.

Производная характеризует скорость изменения функции при изменении аргумента; в частности: производная времени является мерой скорости изменений, используемой по отношению к различным физическим величинам. Например, мгновенная скорость vнеравномерного прямолинейного движения является производной от функции, выражающей зависимость пройденного путиSот времениt.

Производная сложной функции:

Пусть: 1) функция имеет в некоторой точке х₀производную, 2) функцияимеет в соответствующей точкепроизводнуюв упомянутой точке х₀ также будет иметь производную, равную произведению производных функцийи:или короче.

Правила дифференцирования:

1. , 2) , 3) , 4) все они доказываются из соответствующих правил для производных:

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

16. 

17. 

18. 

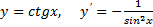
Пусть имеем функцию , определенную в некотором промежутке Х и непрерывную в рассматриваемой точкех₀.Тогда приращениеаргумента отвечает приращение; бесконечно малое вместе с. Большую важность имеет вопрос, существует ли длятакая линейная относительнобесконечно малая, что их разность оказывается, по сравнению с, бесконечно малой высшего порядка:.(1). Приналичие равенства (1) показывает, что бесконечно малаяэквивалентна бесконечно малойи значит, служит для последней ее главной частью, если за основную бесконечно малую взята. Если равенство (1) выполняется, то функцияназывается дифференцируемой (при данном значении х=), само же выражениеназывается дифференциалом функции и обозначается символомТ.О. дифференциал функции характеризуется 2 свойствами: (а) он представляет линейную однородную функцию от приращенияаргумента и (б) разнится от приращения функции на величину, которая приявляется бесконечно малой, порядка высшего, чем.

Пусть функция определена в некоторой окрестности точкиэта функция называется дифференцируемой в точкеесли ее можно представить в виде

, гдеA– некоторое число.

Пусть функция определена на интервалеэта функция имеет производную на интервалеесли она имеет производную в каждой точкет. е. эта функция дифференцируема в каждой точкев этом случае также говорят, что функциядифференцируема на интервале.

Уравнение касательной к графику функции