Лист Мёбиуса
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Лента Мёбиуса
Лист Мёбиуса (ле́нта Мёбиуса, петля́ Мёбиуса) — топологический объект, простейшая неориентируемая поверхность с краем, односторонняя при вложении в обычное трёхмерное евклидово пространство R³. Попасть из одной точки этой поверхности в любую другую можно, не пересекая края.
Лента Мёбиуса была открыта независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 году. Модель ленты Мёбиуса может легко быть сделана. Для этого надо взять достаточно вытянутую бумажную полоску и соединить концы полоски, предварительно перевернув один из них. В евклидовом пространстве существуют два типа полос Мёбиуса в зависимости от направления закручивания: правые и левые (топологически они, однако, неразличимы).
|
Содержание
|
Свойства
Если разреза́ть ленту вдоль по линии, равноудалённой от краёв, вместо двух лент Мёбиуса получится одна длинная двухсторонняя (вдвое больше закрученная, чем лента Мёбиуса) лента, которую называют «афганская лента». Если теперь эту ленту разрезать вдоль посередине, получаются две ленты, намотаные друг на друга.
Если разреза́ть ленту Мёбиуса, отступая от края приблизительно на треть её ширины, то получаются две ленты, одна — более тонкая лента Мёбиуса, другая — длинная лента с двумя полуоборотами (Афганская лента).
Другие интересные комбинации лент могут быть получены из лент с двумя или более полуоборотами в них. Например если разрезать ленту с тремя полуоборотами, то получится лента, завитая в узел трилистника. Разрез ленты с дополнительными оборотами даёт неожиданные фигуры, названные парадромными кольцами.
Геометрия и топология
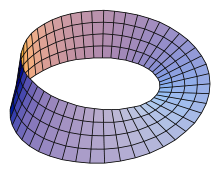
Параметрическое описание листа Мёбиуса.
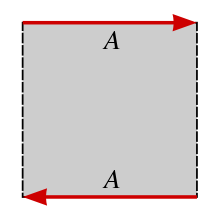
Чтобы превратить квадрат
в лист Мёбиуса, соедините края, помеченные
так,
чтобы направления стрелок совпали.
Одним из способов представления
листа Мёбиуса как подмножества
является
параметризация:
где
и
.
Эти формулы задают ленту Мёбиуса ширины
1, чей центральный круг имеет радиус 1,
лежит в плоскостиx
- y
с центром в
.
Параметрu
пробегает вдоль ленты, в то время как v
задает расстояние от края.
В цилиндрических
координатах
,
неограниченная версия листа Мёбиуса
может быть представлена уравнением:
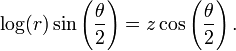
Топологически
лист Мёбиус может быть определен как
факторпространство
квадрата
поотношению
эквивалентности
для
.
Лист Мёбиуса — неориентируемая поверхность с краем.
Лист Мёбиуса — это также пространство нетривиального расслоения над окружностью с слоем отрезок.
Подобные объекты
Близким «странным» геометрическим объектом является бутылка Клейна. Бутылка Клейна может быть получена путём склеивания двух лент Мёбиуса по краям. В обычном трёхмерном евклидовом пространстве сделать это, не создавая самопересечения, невозможно.
Другое похожее множество —
сфера
с плёнкой.
Если проколоть отверстие в сфере с
плёнкой, тогда то, что останется, будет
листом Мёбиуса. С другой стороны, если
приклеить диск к ленте Мёбиуса, совмещая
их границы, то результатом будет сфера
с плёнкой. Чтобы визуализировать это,
полезно деформировать ленту Мёбиуса
так, чтобы её граница стала обычным
кругом. Такую фигуру называют «пересечённая
крышка»
(пересечённая крышка может также означать
ту же фигуру с приклееным диском, то
есть погружение проективной
плоскости в
).
Существует распространённое
заблуждение, что пересечённая крышка
не может быть сформирована в трёх
измерениях без самопересекающейся
поверхности. На самом деле возможно
поместить ленту Мёбиуса в
с
границей, являющейся идеальным кругом.
Идея состоит в следующем: пустьC
будет единичным
кругом в
плоскости xy
в
.
Соединивантиподные
точки на C,
то есть, точки под углами θ
и θ + π
дугой круга, получим, что для θ
между 0
и π/2
дуги лежат выше плоскости xy,
а для других θ
ниже (причём в двух местах дуги лежат в
плоскости xy).
Можно заметить, что если диск приклеивается к граничной окружности, то самопересечение получающейся сферы с плёнкой неизбежно в трёхмерном пространстве. В терминах задания сторон квадрата, как было показано выше, сфера с плёнкой получается склеиванием двух оставшихся сторон с сохранением ориентации.