Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Таврический Национальный Университет им. В.И. Вернадского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Algebra_10kl_RU

.pdf

Скачиваний:

116

Добавлен:

20.03.2015

Размер:

5.2 Mб

Скачать

☆

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 4243 / 4543 44 45 > Следующая >>>

								Т а б л и ц а 4

		Нахождение области определения функции

	Вид функции				Ограничения, которые учитываются
	Вид функции		при нахождении области определения функции*
			при нахождении области определения функции*
1	y =	f (x)	g (x) ≠ 0			Знаменатель дроби не равен нулю
1	y =	g (x)	g (x) ≠ 0			Знаменатель дроби не равен нулю
		g (x)

	y = 2k f (x)		f (x) l 0			Под знаком корня четной степени
2	y = 2k f (x)					может стоять только неотрица
2	(k N)					может стоять только неотрица
	(k N)					тельное выражение

	y = lg (f (x))		f (x) > 0			Под знаком логарифма может сто
3	y = lg (f (x))		f (x) > 0			ять только положительное выра
						жение
4	y = log f (x) a		f (x) > 0,			В основании логарифма может сто
4	y = log f (x) a					ять только положительное выраже
	(a > 0)		f (x) ≠ 1			ние, не равное единице
			f (x) ≠	π	+ πk,	Под знаком тангенса может сто
5	y = tg (f (x))		2			ять только выражение, не равное
			(k Z)				π	+ πk (k — целое)
			(k Z)			2		+ πk (k — целое)
						2
	y = ctg (f (x))		f (x) ≠ πk,			Под знаком котангенса может сто
6			f (x) ≠ πk,			ять только выражение, не равное πk
6			k Z			ять только выражение, не равное πk
			k Z			(k — целое)
						(k — целое)

7	y = arcsin (f (x))		\| f (x) \| m 1,			Под знаками арксинуса и арккоси
			то есть			нуса может стоять только выраже
8	y = arccos (f (x))		то есть			ние, модуль которого меньше или
						ние, модуль которого меньше или
			–1 m f (x) m 1 равен единице
	y = xα
	а) α — натуральное		x — любое число

	б) α — целое отрица		x ≠ 0

9тельное или нуль

	в) α —нецелое поло	x l 0
	жительное число

	г) α — нецелое отри	x > 0
	цательное число	x > 0
	цательное число

* При записи этих ограничений предполагаем, что функции f (x) и g (x) определены на рассматриваемом множестве.

422

Т а б л и ц а 5

Основные свойства числовых равенств и неравенств

Свойства числовых равенств

Свойства числовых неравенств

1. Если a = b, то b = a

Если a > b, то b < a

Если a = b и b = c, то a = c

Если a > b и b > c, то a > c

(транзитивность равенства)

(транзитивность неравенства)

Если a = b, то a + c = b + c

Если a > b, то a + c > b + c

Если a = b и c = d, то a + c = b + d

Если a > b и c > d, то a + c > b + d

Если a = b и с ≠ 0, то ac = bc

a) Если a > b и с > 0, то ac > bc

б) Если a > b и с < 0, то ac < bc

Если a = b и c = d, то ac = bd

Если a > b (a > 0, b > 0) и c > d

(c > 0, d > 0), то ac > bd

Если a = b, то an = bn

a) Если a > b (a > 0, b l 0),

то a2k > b2k

б) Если a > b, то a2k + 1 > b2k + 1

а) Если a = b (a l 0, b l 0),

а) Если a > b (a > 0, b > 0),

то 2k a = 2k b

то 2k a > 2k b

б) Если a = b, то 2k+1 a = 2k+1 b

б) Если a > b, то 2k+1 a > 2k+1 b

Если a = b, a ≠ 0, b ≠ 0, то

Если a > b (a > 0, b > 0), то

a b

10.

a) ab > 0 тогда и только тогда,

10.

ab = 0 тогда и только тогда,

когда a > 0 и b > 0

или a < 0 и b < 0

когда a = 0 или b = 0

б) ab < 0 тогда и только тогда,

когда a > 0 и b < 0

или a < 0 и b > 0

11.

> 0 тогда и только тогда,

11.

= 0 тогда и только тогда,

когда a > 0 и b > 0

или a < 0 и b < 0

когда a = 0 и b ≠ 0

б)

< 0 тогда и только тогда,

когда a > 0 и b < 0

или a < 0 и b > 0

423

(π5k , k ≠ 0, k Z);

ОТВЕТЫ И УКАЗАНИЯ

		Раздел 1
§ 1. Пункт 1.1. 1. 1) 2,5; –2; 3	1	; a +	1	; 2) –3; –2; 1; b2 – 3; 3) 1; 2; 0; m + 1.
			a
3

2. 1) R; 2) [–3; +×); 3) х ≠ –1; 4) R; 5) (–×; –1] [1; +×); 6) R; 7) [1; 5]; 8) [–3; 0) (0; +×); 9) [–3; 3) (3; +×); 10) (–×; –1) (–1; 0] [1; +×); 11) [0; 2) (2; +×); 12) R. 3. 1) {5}; 2) R; 3) [0; +×); 4) [0; +×); 5) R; 6) [–5; +×); 7) [3; +×). 4. а) D (f)= [–3; 5]; E (f) = [–3; 2]; возрастает: [–2; 3]; убывает: [–3; –2] и [3; 5]; f (1) = 0; б) D (f) = [0; 6]; E (f) = [0; 4]; возрастает: [0; 2] и [5; 6]; убывает: [2; 5]; f (1) = 2. 10. 1) Возрастающая; 2) убывающая; 3) возрастающая; 4) убывающая. 11. 2) 4. Пункт 1. 2. 1. 3) четная; 4) нечет% ная; 5) четная и нечетная; 6) нечетная. 2. 1) k > 0, b > 0; 2) k < 0, b < 0; 3) k > 0, b < 0. 6. 1) a < 0, b > 0, c > 0; 2) a > 0, b < 0, c < 0; 3) a < 0, b > 0, c < 0; 4) a > 0, b < 0, c > 0.

	5π			;			π				5π					4π			π				5π
§ 2. 3. 1) 4					2)			; 3)				; 4)			−		; 5) −				; 6) −			. 4. 1) 540°; 2) 135°; 3) –72°;

						5				9					3				8				6
4) 210°; 5) –10°; 6) 330°; 7) –22,5°; 8)																		540°		.

§ 3. 1. 3) ІІІ; 4)						ІІІ; 5) ІII; 6) ІV.												π

§ 4. 1. 1)		1	;		2)	−			1	; 3) −			1	;	4) 1; 5)				2			; 6)	3		; 7) –1; 8) 3. 2. 2) Т = π;

2						2				3									2				2

4) T = π ; 5) Т — любое действительное число, кроме 0. Наименьшего положи%

тельного числа не существует. 3. 1) π (πk, k ≠ 0, k Z); 2) π

3) 3π (3πk, k ≠ 0, k Z); 4)	π	(	πk	, k ≠ 0, k Z); 5) 5π (5πk, k ≠ 0, k Z).

3		3

§ 5. 5. 1) sin 3,9, sin 3,3, sin 1,2; 2) cos 1,9, cos 1,2, cos 0,3; 3) tg (–1,3), tg 0,7, tg 1,5; 4) ctg 2,9, ctg 1,1, ctg 0,5.

§ 6. 1. 1) Нет; 2) да; 3) нет; 4) да; 5) да; 6) да. 2. 1)											cos α =			5	, tg α = –2,4,
§ 6. 1. 1) Нет; 2) да; 3) нет; 4) да; 5) да; 6) да. 2. 1)											cos α =				, tg α = –2,4,
											13					2
ctg α = −		5	;	2) sin α = 0,6, tg α = –0,75,					ctg α = −1			1	; 3) cos α = −			2	,
ctg α = −		5	;	2) sin α = 0,6, tg α = –0,75,					ctg α = −1			1	; 3) cos α = −			13	,
12											3					13
sin α = −	3			, ctg α =	2	; 4) sinα =	5	, cos α = −	1	, tg α = –5. 3. 1) 0; 2) sin2 α;
13				3			26		26


3) 1; 4) –cos2 α; 5) 1; 6)	0; 7) sin α; 8) 1; 9)							2	; 10) –2 tg α. 5. 1) −								3	;	2) а) 2; б) 2.
3) 1; 4) –cos2 α; 5) 1; 6)	0; 7) sin α; 8) 1; 9)								; 10) –2 tg α. 5. 1) −									;	2) а) 2; б) 2.
						3										8
§ 7. Пункт 7.1. 1. 1)		1	; 2)	1	; 3)	3	; 4)			1	; 5)	1	; 6)	1	; 7)	1		;	8)	3	; 9) 1;
	2			2		2			2		2			2		2			2

10) 3; 11) 1 . 2. 1) sin 2α; 2) cos 2α; 3) sin α; 4) cos β; 5) сtg 3α; 6) tg 6α;

424

7) tg 7α; 8) tg 5α; 9) tg α сtg β; 10) tg (α – β). 3. 1)																																		3 + 1				; 2)				3			− 1	; 3) 2 +										3;
																																										3			− 1
																																	2			2						2			2
																																	2			2

4)			3 + 1			; 5)		1 −					3	; 6) −2 −							3. Пункт 7.2. 1. 1)										3	; 2)				1			; 3)			1		1	; 4)			1		;			5)	1					;
			3 + 1					1 −					3																		3													1				1
																														2						2											2
	2			2				2				2																		2						2						2					2									3
	2			2				2				2
6)	1		.	4. 1) sin α; 2) sin												2		α; 3) 2sin α; 4)									1						. 5. 1) −							24		; 2) −					7					; 3)		3		3			;
	2																																							25							25									7
																										cos 2α + sin 2α
																										cos 2α + sin 2α
4)		7		. 6. 1)					120			;	2)		−	119				;	3) −1			1	; 4)		−	119	.	7. 1)					24		; 2)				7		;		3) 3				3		;		4)		7			.
4)	24			. 6. 1)				169				;	2)		−					;	3) −1				; 4)		−		.	7. 1)							; 2)			25			;		3) 3						;		4)	24				.
	24							169							169						119						120						25							25							7							24
8. 1)				−	24		; 2)			7	;		3)		−3		3		; 4) −			7	.9. –0,8. 10. –1,125; 0. Пункт 7.3. 1. 1) −																																	3	;
8. 1)				−			; 2)	25			;		3)		−3				; 4) −				.9. –0,8. 10. –1,125; 0. Пункт 7.3. 1. 1) −																																	3	;
				25				25								7					24																																	2

			3	; 4) –1; 5)	−	1	; 6)	1	;	1
2) −	3;	3)								7)

								2
		2			2					3

; 8) 1. 2. 1) 2 ; 2) 3 . 3. 1) cos2 α;

2) –cos2 α; 3)	−	1	; 4)	1	ctg2 α; 5) 1. Пункт 7.4. 1. 1) 0; 2) –sin 18°; 3) 2 sin25°;
				2
	2

4)tg 20° ctg 5°;5)sin (α – β) sin (α +β);6) 4sin 5α cos α cos α; 7) 4cos 5α cos α cos α.

									2		2					2		2
	3 + 1		2 − 1			1		3		1	(cos	π	+ cos	3π	).		1		1
3. 1)	3 + 1	; 2)	2 − 1	;	3)	1	cos 10° −	3	; 4)	1	(cos	π	+ cos	3π	).	4. 1)		; 2)		.
4			4			2		2		2		10		10			2		2

§ 10. Пункт 10.1. 1. 1) a = 4, b = 5, c = 0, d = 1; 2) a = 2, b = 0, c = 1, d = 2.

2. a = 0, b = −	1	,	c =	1	. 5. a = 1, b = 2. 6.	a =	6	,	b = −	10	. Пункт 10.2.

2			2			11			11

1. 1) 3x2 + x + 4; 2) x8 – x6 + x4 – x2 + 1; 3) x3 – 2x2 + 4x – 2. 2. 1) Q (x) = 4x2 –

– 6x – 1, R (x) = 12x + 3; 2) Q (x) = x3 + 2x2 + 5x + 10, R (x) = 20x + 21. 3. 1) a = –18, b = –35; 2) a = –8, b = 20; 3) a = –1, b = –2. 4 .1) Q (x) = x + 6, R (x) = 12x + 12; 2) Q (x) = x, R (x) = –20x – 30. Пункт 10.3. 1. –101. 2. а = –3.

3. х + 3. 4. a = –1, b = 1. 5. 8; 5 2 . 7. –2x3 + 8x2 + 14x – 20. 8. a = –2. 9. 3.

10. 2x3 – 10x2 + 6x + 18. 11. a = 3, b = 9. 12. x2 + 5x + 1 = 0. 13. x2 – 5x + 2 = 0. 14. x2 – 30x + 9 = 0. Пункт 10.4. 1. 1) Q (x) = x2 + 2x + 1, R (x) = 0; 2) Q (x) = = 5x2 – x + 20, R (x) = 96; 3) Q (x) = x2 – 18x + 64, R (x) = –168. 2. 1) Да; 2) да. 3. 1) 2x2 – 5x – 3; 2) 2x2 – 11x + 5. Пункт 10.5. 1. 1) 1; 2) –3; 2; 3) –4; 4) –2; 1.

2. 1) 1; 2) –0,5; 3) ä1; − 2 ; 4) –1; 2. 3. 1) (2x + 1)(x + 1)(x – 2); 2) (x + 1)(x +

+ 3)(x + 5); 3) (x – 1)3(x + 1); 4) (x – 1)2(x + 5)(x – 5). 4. 1) 1; −1± 3; 2) –2;

–1; 3; 3) –0,5; 1; 4) 0,5; 1± 2. У к а з а н и е. Сначала найти рациональный корень (x = α) многочлена и разделить многочлен на x – α. 5. 1) (x2 + 3x – 2)×

×(x2 – 2x + 3); 2) (x2 + 3x – 1)(x2 – 7x + 2). 6. 1) (x2 +																	2x + 1− 2)(x2 −				2x + 1+ 2);
2)	((	+	2	)	x	2	−	)	(	(	)	2	) –	)	3)	(	x	2	+ 2x + 1	− 2	)(	x	2	+ 2x +
	1							2x + 1			2 −1 x			2 −1 ;

+ 1+ 2).

425

																									α	2
§ 11. Пункт 11.1. 1. 1)										2 − 2		;		2)		2+ 2	;	3)		2 − 1.	2. 1)			sin	2 =			;
										2 − 2						2+ 2										5
									2							2
									2							2
cos α = −			1	;	tg α = −2;			2)	sin α =			2			;	cos α = −		3	;	tg α = −		2	.	3.	3 + 2		2.
cos α = −				;	tg α = −2;			2)	sin α =						;	cos α = −			;	tg α = −			.	3.	3 + 2		2.
2	5				2				2			13				2		13		2	3
4. −	2	. 5. 0,6. 6. −				1	.	7. 2. 8.			−1 +	5	. У к а з а н и е. Если α = 18°, то 36° = 2α
						1

	13				3				4
и 54° = 3α (где sin α > 0).

Дополнительные упражнения. 1. 1) 0; 2) | sin β + cos β |; 3) 13; 4) sin β.

2. 1) 2tg α; 2) –1; 3) 1; 4) 1. 7. 1)	7	; 2)	1	; 3)	−1 + 17	. У к а з а н и е. Из
9			(m + 1)2	4

условия следует, что											1− cos2 α								= 1, где \| cos α \| 1; 4) sinα = −																					2 2		, cos2α = −								7			,
условия следует, что											1− cos2 α								= 1, где \| cos α \| 1; 4) sinα = −																							, cos2α = −											,
cos α = −		1											cosα							2																				3									9
		1		.
				.
2	3																					Раздел 2
	3

§ 12. 1. 1)					y =		1		x + 2, D = R, E = R; 2)																	y = −					1	x − 2,			D = R, E = R; 3) y =														2		,
§ 12. 1. 1)					y =				x + 2, D = R, E = R; 2)																	y = −						x − 2,			D = R, E = R; 3) y =																,
					3																									3																			x
D: х ≠ 0, E: у ≠ 0; 4)												y = −				1		,		D: х ≠ 0, E: у ≠ 0; 5) y = x2, D = [0; +×),
D: х ≠ 0, E: у ≠ 0; 4)												y = −						,		D: х ≠ 0, E: у ≠ 0; 5) y = x2, D = [0; +×),
																x
E = [0; +×). 3. 1) y = 2													x; 2) y = −2										x; 3) y =								x + 2; 4) y = −										x + 2.
§ 13. 1. 1) 0; 2)								π		; 3)		π		; 4)			π		; 5) − π ; 6)							−	π	.		2. 1) 0; 2)						π	; 3)			π	; 4)			−	π		. 3. 1)			π		;
§ 13. 1. 1) 0; 2)										; 3)				; 4)		3			; 5) − π ; 6)							−		.		2. 1) 0; 2)							; 3)			3	; 4)			−			. 3. 1)		2			;
					2							4				3							2			4									4					3				3					2
2) 0; 3)	π		; 4)		π	; 5) π; 6)							3π		. 4. 1)						π	;	2)	π	;	3)			π	; 4)			5π	.	5. 1)			2	; 2)				2	6		; 3)		1			;
	4				6							4								2			3			6				6					7									5				15

4)	3	.	6. 1) 7; 2) 3; 3)	3
	4			10

;	4)	1	.	7. 1)	2	;	2)	2 2	; 3)	1	1	;	4)	1	. 8. 1) 7;	2) 1,5;

		3			7			3		3				2 6


3)	1	;	4)	3	.	9. 1)			π	; 2) 7 – 2π; 3)	π	; 4) 8 – 2π; 5)		π		; 6) 4 – π; 7)		π	; 8) 10 – 3π.
	26	;		5	.				7		5			5				9
	26			5					7		5			5				9
	§ 14. 1. 1) ±						π	+ 2πn, n Z; 2) корней нет; 3)					±		2π		+ 2πn, n Z; 4) ±			3π	+ 2πn,
	§ 14. 1. 1) ±							+ 2πn, n Z; 2) корней нет; 3)					±		2π		+ 2πn, n Z; 4) ±				+ 2πn,
						4										3			4

n Z. 2. 1) (−1)n π + πn, n Z; 2) (−1)n π + πn, n Z; 3) (−1)n+1 π + πn, n Z;

6 3 6

4) корней нет. 3. 1)

+ πn, n Z; 2)

+ πn, n Z; 3) − π + πn, n Z; 4) −

+ πn,

n Z. 4. 1)

+ πn, n Z; 2)

+ πn, n Z; 3)

3π

+ πn,

n Z; 4)

5π

+ πn,

n Z. 5. 1) (–1)n + 1 arcsin 0,6 + πn, n Z; 2) äarccos 0,3 + 2πn, n Z;

3) – arctg 3,5 + πn, n Z; 4) arcctg 2,5 + πn, n Z. 6. 1)

+ πn, n Z; 2)

πn

n Z; 3)

πn

, n Z; 4)

arctg 3 +

πn

n Z. 7. 1)

(–1)n π + 4πn, n Z;

426

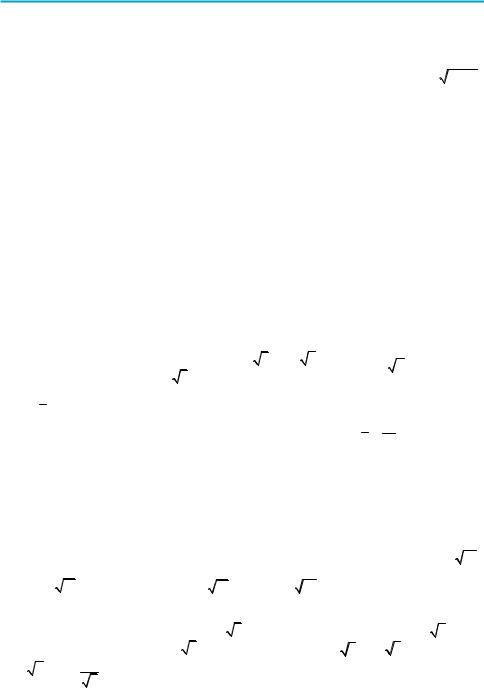
2) ± 15π + 10πn, n Z; 3) − π + 3πn, n Z; 4) 7π + 7πn, n Z. 8. 1) (−1)n π + πn ,

4 2 4 8 2

(

2π

πn

Z; 2) ä2π + 6π n,

Z; 3)

−1

+ 4πn,

Z; 4)

(

)n+1

3π

5π

π πn

3π

9. 1)

−1

+ 3πn, n

Z; 2) ± 12 + πn, n

Z; 3) −

, n

Z; 4)

2 + 2π ,

n Z. 10. 1)

2π

+ 4πn,

4πn, n Z; 2)

+ 3πn, n Z; 3)

2πn

, n Z;

4) −

2π

+ 4πn, n Z. 11. 1) −

5π

− πn, n Z; 2) π – 2πn, n Z; 3) –8πn;

−

4π

− 8πn,

n Z; 4) −

2πn

;

−

2πn

, n Z. 12. 1)

;

3π

;

11π

;

17π

;

19π

; 2) ±

; ±

11π

;

13π

; 3)

−

5π

;

7π

; 4)

3π

;

7π

;

11π

;

15π

13. 1) −

17π

;

−

13π

;

−

5π

;

−

;

7π

;

11π

;

19π

; 2) 0; ä2π; 4π; 3) 0; 2π; 4π; 4)

5π

;

11π

;

13π

;

19π

;

7π

§ 15. 1. 1)

(−1)n+1 arcsin

+ πn,

n Z; 2)

(−1)n+1

arcsin

πn

, n Z;

3) (−1)n arcsin

+ πn, n Z; 4) π + 4πn, (−1)n

+ 2πn, n Z. 2. 1)

2π

+ 2πn;

± arccos

+ 2πn, n Z; 2) ±

2π

2πn

, n Z; 3) π + 2πn, n Z; 4) äπ + 6πn, n Z.

3. 1)

2π

+ 2πn, n Z; 2)

+ πn,

n Z; 3)

+ 2πn,

(−1)n arcsin

+ πn, n Z;

2πn

πn

arcctg 5 +

πn

4) 6

+ 3

, n

Z. 4. 1) −

4 + πn,

arctg 3

+ πn, n

Z; 2)

+ 2 ,

n Z; 3) –arctg 2 + πn, arctg

+ πn, n Z; 4)

3π

+ 2πn,

2arcctg

+ 2πn, n Z.

)+ 2πn,

5. 1)

(−1)n arcsin

+ πn, n Z; 2) ± (π − arccos

n Z. 6. 1)

+ πn,

–arctg 3 + πn, n Z; 2)	π	+ πn, arctg 3 + πn, n Z; 3)	π	+ πn; –arctg 2 + πn, n Z;

4		4

4) − π + πn, arctg			2	+ πn, n Z. 7. 1) π + 2πn, ±					2π	+ 4πn, n Z; 2) arctg							1 ± 5	+ πn,

4	3						3							2
n Z; 3)	π	− arcsin			5	+ 2πn, n Z; 4)	π	+ πn, (−1)n arcsin					3	+ πn, n Z. 8. 1) 2πn,
							2
	2			13								4
π + 4πn, n Z; 2) 4πn, π + 2πn, n Z; 3) (−1)n arcsin											1	+ πn, n Z; 4)			π	+ πn, n Z.

							3							6

9. 1) −	π	+ πn, n Z; 2)	π	+ πn, arctg 2 + πn, n Z; 3)	π	+ πn, arctg 3 + πn, n Z;
4		4		4
				427

4) arctg	−7 ±	53	+ πn, n Z. 10. 1) ±	2π	+ 2πn, n Z; 2)	(−1)n+1	π	+ πn, n Z;

2		3				6

(−1)n

+ πn, n Z; 4) ±

+ 2πn, n Z. 11. 1) −

+ πn, n Z; 2)

3π

+ πn, n Z;

+ πn, n Z; 4)

+ πn, n Z. 12. 1)

+ 2πn, n Z; 2) 2πn, n Z; 3) πn;

+ πn, n Z; 4)

+ πn;

+ πn, n Z. 13. 1) (−1)n

+ πn, n Z; 2)

+ 2πn,

n Z; 3) ± arctg

2 + πn, n Z; 4) arctg 2 + πn; − arctg

+ πn, n Z. 14. 1)

πn

n Z; 2) πn;

πn

, n Z; 3)

πn

, n Z; 4)

πn

, n Z. 15. 1) ±

+ πn, n Z;

2) ±

πn

, n Z. 16. 1)

−

+ πn , n Z; 2) 2πn, n Z. 17. 1)

+ πn, n Z;

2) − π + πn, n Z. 18. 1)

+ πn; –arctg 2 + πn, n Z; 2) −

πn

, −

arctg 3 + πn ,

n Z; 3)

+ πn, –arctg 3 + πn, n Z; 4) −

πn

−

arctg 4 +

πn

n Z.

19. 1)

+ 2πn, –2 arctg 2 + 2πn, n Z; 2)

+ 2πn,

−2arctg

+ 2πn, n Z; 3) πn,

−

+ πn, n Z; 4)

+ πn, − arctg

+ πn,

n Z. 20. 1)

(−1)n+1

+ πn,

n Z;

2) (−1)n

+ πn, n Z; 3) π + 2πn, ±

+ 2πn, n Z; 4)

2πn

, n Z.

§ 16. 1. 1)

(

+ 2πn;

5π

− 2πn),

(

5π

+ 2πn;

− 2πn), n Z; 2) (

+ 2πn;

−

+ 2π(1 − n)), (

−

+ 2πn; π + 2π(1− n)), n Z. 2. 1) (πn;

− πn),

(

+ πn;−πn),

n Z; 2) (−2πn; −

− 2πn),

(−

2π

− 2πn; − π − 2πn), n Z. 3. 1) (

+ 2πn;

(−1)k+1 π + πk),

((−1)n+1

+ πn;

+ 2πk), k, n Z; 2) (π + 2πn; ± π + 2πk),

(±

+ 2πn; π + 2πk), k, n Z. 4. 1)

((−1)n

+ πn; ±

2π

+ 2πk),

((−1)n+1

+ πn;

+ 2πk), k, n Z; 2)

(arctg

+ πn; π − arctg

− πn), (arctg

+ πn; π − arctg

−

)

n Z. 5. 1)

(

+ π(k + n);

+ π (k − n)), (−

+ π(k + n); −

+ π(k − n)),

−πn ,

k, n Z; 2) (

+ π(n + k);

+ π(n − k)),

(

2π

+ π(n + k); −

+ π(n − k)), k, n Z.

5π

+ π(k − n)), k, n Z; 2) (

6. 1) (

+ π(k + n);

+ π(k − n)), (

+ π(k + n);

428

+π(n + k); −

+ π(n − k)), (

5π

+ π(n + k); −

5π

+ π (n − k)), k, n Z. 7. 1) (

+ 2πn +

+ πk),

πk

;

πk

), k, n Z; 2)

(

+ 2πn − πk ;

πk

k, n Z. 8. 1)

(2πn;

k, n Z; 2)

(

+ 2πn;

+ πk), k, n Z.

§ 17. 2. 1) а) Да; б) да; 2) а) да; б) нет. 6. 1) Да; 2) да; 3) нет; 4) да; 5) нет.

7. 1) 323; 2) –4; 3) – 4; 4) –3; 23. 8. 1) Корней нет; 2) 2; 3) − 2; 4) корней нет.

9. 1) х ≠ 1,5 (условие для корней); 2) х l 0. 11. 1) 7; 2) 0; 4,5; 3) − 2 ; 4) − 1 .

3 3

§18. 1. 1) 2; 2) 3; 3) (1; 0). 2. 1) 0; 2) 0; 3) –1; 4) 0,5. 3. 1) 3; 2) (–2; 5);

3)(3; 1); 4) корней нет; 5) (2; 1); 6) (–1; 2; –3). 4. 1) 6; 2) 1; 3) 0; 4) 6; 5) 2;

−

; −

6) 1. 5. 1) (–5; –5); (2; 2);

(–2; –2); 3)

;

4) (–2; –2); (2; 2).

§ 19. 1. 1)

(−1)n+1 π + πn,

+ 2πn,

n Z; 2)

+ 2πn,

π + 2πn,

n Z.

3π

2. 1)

+ 2πn,

n Z; 2) корней нет; 3) 3 + 4n, n Z; 4) 1; 5)

+ πn,

n Z.

;

3. 1)

2 + πk, arctg 11 + πn, k, n

Z; 2)

+ πk, ± arctg

2 + πn, k, n

Z. 4. 1)

2) (0,5; π + 4πn), (–0,5; π – 4πn), n Z. 5. 1) 1; 2) –0,25; 3) 1; 4) 1; 5) 0,125;

6) 0; ä1. 6. 1)

(−

+ π(2k − n);

− πn),

(

+ π(2k + n); −

+ πn),

k, n Z;

2) (

5π

(4k + n);

+ πn ), k, n Z; 3) ((−1)n+1

+ πn; ±

+ 2πk);

((−1)n

+ πn;

2π

+ 2πk), k, n Z; 4) (

πk

; ±

+ 2πn), k, n Z; 5) (

+ 2πn;

2π

+ 2πk),

(

2π

+ 2πn; π + 2πk), (−

+ 2πn; −

2π

+ 2πk),

(−

2π

+ 2πn; −

+ 2πk), k, n Z; 6) (πn;

πk), (–0,5 arccos (–0,75) + πn; –0,5 arccos (–0,75) + πk), (0,5 arccos (–0,75) + + πn; 0,5 arccos (–0,75) + πk), (–0,5 arccos 0,25 + πn; –0,5 arccos 0,25 + πk), (0,5 arccos 0,25 + πn; 0,5 arccos 0,25 + πk), k, n Z. У к а з а н и е. Предста%

4sin(3x + 2y) = − sinx,

вить систему в виде = − ( + ) и перемножить соответственно пра%siny 4sin 2x 3y

вые и левые части полученных уравнений. Учесть, что при таких преобразо% ваниях возможно появление посторонних решений системы. При решении промежуточного уравнения 4 sin 5x + sin x = 0 удобно воспользоваться тем, что sin 5x = sin (x + 4x).

429

§ 20. 1. 1) При –1 < a < 1 корней нет; при a m –1 или a l 1

x = (−1)n arcsin	1	+ πn, n Z; 2) при –0,5 ma m0,5, x =	π	+ πn, n Z; при a < –0,5
	a
		2

или a > 0,5 x =	π	+ πn, x = (−1)n arcsin	1	+ πn,	n Z; 3) при a = 0 или a < –1 или

2			2a
a > 1 x = πn, n Z; при –1 ma < 0 или 0 < a m1 x = πn, x = äarccos a + 2πn, n Z;

4) при –1 < a < 1	x =	π	+ πn,	n Z; при a m –1 или а l 1	x =	π	+ πn,

	2				2

x = (−1)n arcsin 1 + πn, n Z. 2. 1) При a < –0,5 или a > 4 корней нет; при a = –0,5

x = (−1)n π + πn, n Z; при –0,5 < a m 0 x = (−1)n arcsin	1 ±	2a + 1	+ πn, n Z; при
		2
6

0 < a m 4 x = (−1)n arcsin1 − 2a + 1 + πn, n Z; 2) при a < –1,25 или a l 5 x = πn,

n Z; при a = –1,25 x = äarccos 0,25 + 2πn, n Z; при –1,25 < a < 1 x = πn,

x = ± arccos1 ± 4a + 5 + 2πn, n Z; при 1 ma < 5 x = πn, x = ± arccos1 − 4a + 5 + 2πn,

4 4

n Z; 3) при b = 0 уравнение не определено; при b ≠ 0 и a = 0 x ≠ πk , x R,

					b
k Z; при b ≠ 0 и a ≠ 0 x =	πn	,	n Z, n ≠	ak	, k Z; 4) при a = –1 или

	a			b

2 − 2 2 < a < 2 + 2 2 x = 2πn, n Z; при a < –1 или −1 < a 2 − 2 2, или

a 2 + 2 2 x = 2πn, x = − π + (−1)n+1 arcsin

2 + a

+ πn, n Z. 3. 1) −2 5 a 2 5;

a 2

2) –5 b 5; 3) a R; 4) a R; 5)

4 − π

ma m

4 + π

. 4. 3 −

< a < 3 +

. 5. (0; 1); (1;

1).7.1)Приa<–2x R;при–2 m a < 2 x (arcsin

+ 2πn; π − arcsin

+ 2πn), n Z;

при а l2 решений нет; 2) при a m

x (− arccos

a + 5

+ 2πn; arccos

a + 5

+ 2πn),

5a − 7

n Z; при

< a < 3 х R;при аl3 x (arccos

a + 5

+ 2πn; 2π − arccos

a + 5

+ 2πn),

5a − 7

n Z; 3) при a < –1 х R; при a = –1 x (–π + 2πn, π + 2πn), n Z; при –1 < a < 0

1 −

a + 1

1 −

a + 1

или 0 < a < 3

x − arccos

+ 2πn; arccos

+ 2πn ,

n Z ; при

a = 0 x (−

+ 2πn),

2π

1 −

a + 1

+ 2πn;

Z; при a l 3 x

− arccos

+ 2πn;

1 + a + 1

1 −

a + 1

− arccos

+ 2πn arccos

+ 2πn; arccos

+ 2πn , n Z.

8. 1) –0,5 m a m 0,5; 2)

−

< a <

. 9. 1)a<–2, a=1, a >2;2)a <0, a=1, a >4;3)a=2.

430

10. 1)

(

+ π(k + n);

+ π(k − n)), k, n Z; 2)

(π(k + n);

− 4 + 2πn; 2π − arccos a +

a<–2 x arccos a +

− 4

n Z; при –2 m a m 2

x (−

+ 2πn;

+ 2πn),

π + π(k − n)), k, n Z; 4) при


	(−	π	+ 2πn;		π		+ 2πn),
+ 2πn

	2			2
при a > 2				x (−		π		+ 2πn;

				2

−arccos a −		2
−arccos a −	a		− 4	+ 2πn arccos a −
	2

a	2	− 4 + 2πn; π
a		− 4 + 2πn; π	+ 2πn , n Z.
2		2

§ 21. Пункт 21.1. 1. 1) (–×; –2] (1; 2] (4; +×); 2) (–×; –2) (3; 8);
3) (4; 5]; 4) [–10; –2) (4; +×). 2. 1) [–2; –1] [1; 2]; 2) (− ; − 1)
(−	1	;	1	) (1; + ); 3) (–×; –3] (0; 3]; 4) (–6; 2). 3. 1) (–2; 2) [4; +×);

3		3

2) (–2; –1) или 1; 3) (–×; 0) [2; 3]; 4) (–×; –1) [4; +×). Пункт 21.2. 1. 1) − 2 ;

4; 2) 0,5; 3,5; 3) –1; 2; 3; 6. 2. 1) (–×; –1) (4; +×); 2) (–0,8; 2); 3) (−3; − 1)

(−1; −	1	); 4)	(−2;2	2	).		3. 1)				1	; 2)	–1; –3. 4. 1) [1; 3]; 2)							–8; 12; 3) [–5; 8].

3			3							3			(− ;			)
5. 1) Решений нет; 2) [2; +×); 3)															2		(8;		+ ). 6. 1) [1; 2]; 2) −2		1	; 3.

														3						3
7. 1) –3; 5; 2) [–1; 4]. 8. 1) −								2	; 0,5; 2; 2) −2 −								5;		5. 9. 1) 0; ä2; 4; 2) –2; 1; 3; 6.

							3
							41							1 +			41
10. 1) (–1; 5); 2) − ;						1 −				(−1; 2)								; + . 11. 1)		(–×; –1) (2; +×);
							2							2

2) [1; 3]. 12. 1) (–5; –2) (–1; +×); 2) (–×; –5) (–3; 3) (5; +×).

13. 1) [–6; –2] [4; 8]; 2) (–×; –8) (2; +×). 14. 1)

(0;

);

2) (–×; –5]

[4; +×). 15. 1)

5; − 4) (−2;0]

− 2 2; − 3) (1; 3].

−3 −

2) −1

§ 22. 1. 1) − 7π + 2πn; π + 2πn ,

n Z; 2) (−

+ 2πn;

5π

+ 2πn), n Z; 3) реше%

1) (−

+ 2πn), n

2π

ний нет; 4)

+ 2πn;

2πn ,

Z. 2.

2πn;

2) (

5π

+ 2πn;

7π

+ 2πn), n Z; 3) R; 4)

−

+ 2πn;

+ 2πn , n Z. 3. 1) (−

+ πn;

+ πn), n

+ πn), n Z; 4) (−

−

+ πn), n Z; 2)

+ πn;

Z; 3) (

+ πn;

+ πn

, n Z.4.1) (πn;

5π

+ πn), n Z;2) (πn; π + πn , n Z;3)

3π

+ πn; π + πn), n Z;

(

+ πn; π + πn), n Z. 5. 1) (

+ πn;

3π

+ πn), n Z; 2)

+ 6πn;

11π

+ 6πn ,

431

<<< < Предыдущая 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 4243 / 4543 44 45 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.08.2019358.53 Кб699354.rtf
#
08.08.20192.1 Mб3agrarne.doc
#
11.11.2019364.54 Кб2ajm_project_description_form_2012_en.doc
#
08.05.20191.03 Mб136ALEXANDER KAMENSK1.doc
#
02.12.20181.91 Mб8ALFRED.doc
#
20.03.20155.2 Mб116Algebra_10kl_RU.pdf
#
20.07.201940.96 Кб1AMERICAN%20VALUES.doc
#
20.03.2015574.46 Кб225anatomia.doc
#
20.03.201531.23 Кб30Antonyme.doc
#
30.04.201583.34 Кб25Arduino Uno Rev.3.pdf
#
20.03.2015693.36 Кб19Art of speaking.docx