
Algebra_10kl_RU
.pdf





РАЗДЕЛ 4. Показательная и логарифмическая функции
10. |
Какой вывод можно сделать о знаке числа х, если: |
||||||
|
1) |
3х = 0,6; |
2) ( |
1 |
)x = 10; 3) 10х = 4; |
4) 0,3х = 0,1? |
|
11. |
6 |
||||||
|
|
|
|
|
|||
Расположите числа в порядке их возрастания: |
|
||||||
|
|
1 |
2− 2, 21,4, 1; |
|
|||
|
1) |
23, 2–1,5, 2 2, |
|
||||
|
|
0,39, 1, 0,3− 5, |
1 |
1 |
|
||
|
2) |
0,32 |
, 0,3–9, 0,33. |
|
|||
12*. Известно, что когда при радиоактивном распаде количество вещества за |
|||||||||
сутки уменьшается вдвое, то через х суток от массы М0 остается масса М, |
|||||||||
которая вычисляется по формуле: M = M |
( |
1 |
)x . Отсюда |
M |
= ( |
1 |
)x . |
|
|
|
M |
|
|
|
|||||
0 |
2 |
|
2 |
|
|
|
|||
|
|
|
|
0 |
|
|
|
|
|
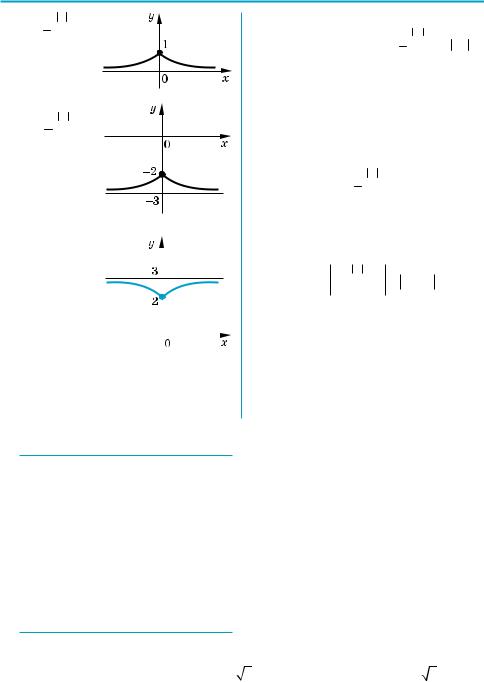
Покажите графически, как с изменением х изменяется отношение |
M |
. |
|||||||
|
|||||||||
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
0 |
|
Используя в случае необходимости построенный график, дайте ответы (точные или приближенные) на вопросы:
а) Во сколько раз уменьшится масса радиоактивного вещества через 1,5 суток, 2,5 суток, 3 суток, 4 суток?
б) Сколько времени должно пройти, чтобы начальная масса радиоактив% ного вещества уменьшилась в 2,5 раза, в 3 раза, в 4 раза?
§30 |
РЕШЕНИЕ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ |
|
|||
И НЕРАВЕНСТВ |
|
|
|||
30.1. ПРОСТЕЙШИЕ ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ |
|
||||
|
|
|
|
|
Т а б л и ц а 50 |
|
|
|
1. Основные формулы и соотношения |
|
|
|
|
|
График функции y = ax (a > 0) |
||
|
|
|
a > 1 |
0 < a < 1 |
a = 1 |
|
auæav = au + v |
|
|
||
|
(ab)u = auæbu |
|
|
||
au |
= au−v, |
(a )u |
= au |
|
|
av |
|
b |
bu |
|
|
|
(au)v = auv |
|
|
|
|
|
|
m |
|
|
|
|
n am = an |
|
|
|
|
|
|
|
возрастает |
убывает |
постоянная |
|
|
|
338 |
|
|



