
Algebra_10kl_RU
.pdf
РАЗДЕЛ 2. Тригонометрические уравнения и неравенства
достаточно решить уравнение sin x = 12 (x = (−1)n 6π + πn, n Z ). Учитывая перио
дичность функции sin x (T = 2π), достаточно записать решение данного неравен ства на одном периоде. На отрезке длиной 2π можно взять, например, такие
абсциссы точек пересечения графиков функций y = sin x и y = |
1 |
: |
x1 |
= |
π |
, x2 |
= |
5π |
2 |
|
|
6 |
|
6 |
|||
(все другие абсциссы точек пересечения отличаются от них на 2πk). Тогда на
одном периоде решениями данного неравенства являются: π < x < 5π (абсцис
6 6
сы выделенных точек графика y = sin x). Все остальные решения данного неравенства получаются прибавлением к найденным решениям чисел вида
2πk, где k Z. Ответ: |
π |
+ 2πk < x < |
5π |
+ 2πk, k Z. |
6 |
|
|||
|
6 |
|
||
Аналогично можно получить и решения других видов простейших нера венств, приведенных в пункте 1 таблицы 41.
Задача 2 Решите неравенство cosx > − 1 .
2
Поскольку cos x — это абсцисса соответствующей точки Рх единичной окружности, то при всех значениях x, которые удовлетворяют данному нера
венству, абсцисса точки Рх больше (− 12 ). Все такие точки на единичной окруж ности (рис. 103) лежат справа от прямой t = − 1 (они изображены на рисунке
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
синей дугой |
P P |
без крайних точек, поскольку в крайних точках cosx = − |
, |
||||||||||||
|
|||||||||||||||
|
x x |
|
|
|
|
|
2 |
|
|||||||
|
1 |
|
2 |
|
|
|
|
|
|
||||||
а не больше − |
1 |
). Если, записывая ответ, двигаться против часовой стрелки, |
|||||||||||||
|
|||||||||||||||
|
2 |
|
|
|
а точка Px — ее концом. Сначала |
||||||||||
то точка Px |
будет началом дуги Px |
Px , |
|||||||||||||
1 |
|
|
|
1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
запишем ответ на одном периоде (напомним, что для косинуса он равен 2π). |
|||||||||||||||
Для точек Рх выделенной дуги x1 < x < x2. Поскольку точка Px2 |
находится |
||||||||||||||
в верхней полуплоскости, то можно взять x |
= arccos (− |
1 |
)= π − π |
= |
2π |
. Учи |
|||||||||
|
|
||||||||||||||
|
|
|
|
|
|
2 |
2 |
3 |
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
тывая симметричность (относительно оси t) точек P |
и P , получаем |
|
|
x2 |
x1 |
|
x1 = −x2 = − 2π . Таким образом, на одном |
|
|
3 |
|
|
периоде решениями данного неравен |
|
|
ства являются − 2π < x < 2π . Через пери |
|
|
3 |
3 |
|
од 2π значения косинуса повторяются. |
|
|
Поэтому все остальные решения данно |
|
|
го неравенства получаем прибавлением |
|
|
к найденным решениям чисел вида 2πk, |
|
Рис. 103 |
где k Z. |
|
252

§ 22. Решение тригонометрических неравенств
Ответ: − 2π + 2πk < x < 2π + 2πk, k Z.
3 3
Рассуждения при использовании графической иллюстрации решения не
равенства cos x > − 1 полностью аналогичны приведенным выше рассужде
2
ниям по решению неравенства sin x > 1.
2
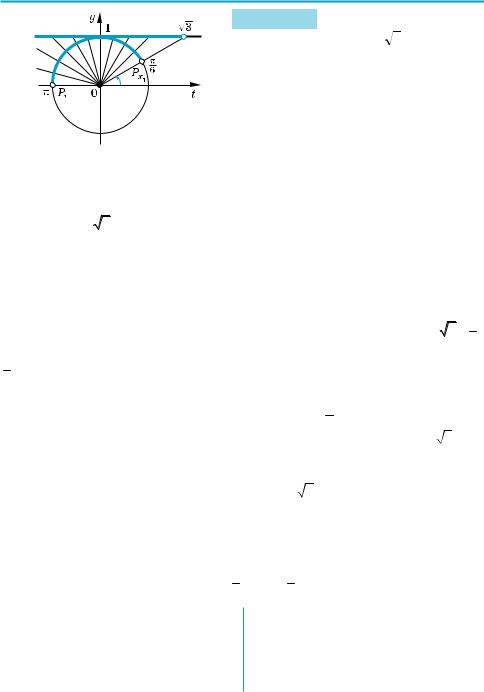
Задача 3 Решите неравенство tg x l –1.
Период тангенса равен π. Поэтому сначала найдем решения этого нера венства на промежутке длиной π, например, на промежутке (− 2π ; 2π ), а потом
используем периодичность тангенса. Для выделения тех точек Рх правой по луокружности, значения x которых удовлетворяют данному неравенству, вос пользуемся линией тангенсов (рис. 104). Сначала выделим на линии танген сов значения тангенсов, большие или равные (–1) (на рисунке они выделены синей линией), а потом для каждой точки линии тангенсов найдем соответ ствующую точку Px на правой полуокружности (для этого достаточно соеди нить центр окружности с выделенной точкой на линии тангенсов и взять точ ку пересечения проведенного отрезка с окружностью). Множество соответству
ющих точек Px единичной окружности выделено на рисунке синей дугой Px1Pπ
2
(обратите внимание: точка Px1 принадлежит рассмотренному множеству, а
точка Pπ |
— нет). Поскольку точка Px находится в правой полуплоскости, то |
|||
2 |
|
|
1 |
|
|
π |
|
||
можно взять x = arctg (−1) = − |
. Таким образом, на одном периоде решения |
|||
|
||||
|
1 |
4 |
|
|
|
|
|
||
ми данного неравенства являются − π mx < π . Через период π значение танген
42
са повторяется. Поэтому все остальные решения данного неравенства полу чаем прибавлением к найденным решениям чисел вида πk, где k Z.
Ответ: − π + πk mx < π + πk, k Z.
42
Заметим, что при решении данного не равенства с использованием графиков до статочно, как и в предыдущих случаях, на
одном периоде (например, на промежутке
(− π2; π2))
соответствующие точки графика функции |
|
y = tg x находятся выше прямой y = –1 или |
|
на самой прямой. (На рисунке в таблице 41 |
|
соответствующие части графика функции |
|
y = tg x выделены синими линиями.) |
Рис. 104 |
253
РАЗДЕЛ 2. Тригонометрические уравнения и неравенства |
|
|||
|
|
Задача 4 |
Решите неравенство |
|
|
|
|
ctg x < 3. |
|
|
|
Период котангенса равен π. Поэтому |
||
|
|
сначала найдем решение этого неравен |
||
|
|
ства на промежутке длиной π, например |
||
|
|
на промежутке (0; π), а потом восполь |
||
|
|
зуемся периодичностью котангенса. |
||
|
|
Для выделения тех точек Px верхней |
||
|
Рис. 105 |
полуокружности, значения x которых |
||
|
удовлетворяют данному неравенству, |
|||
|
|
|||
|
|
воспользуемся линией котангенсов |
||
(рис. 105). Сначала выделим на линии котангенсов значения котангенсов, |
||||
меньшие, чем |
3 (на рисунке 105 они выделены синей линией), а потом для |
|||
каждой точки линии котангенсов найдем соответствующую точку Px на верх |
||||
ней полуокружности (для этого достаточно соединить центр окружности с вы |
||||
деленной точкой на линии котангенсов и взять точку пересечения проведен |
||||
ного отрезка с окружностью). Множество соответствующих точек Px единич |
||||
ной окружности обозначено на рисунке 105 синей дугой Px Pπ. Поскольку точ |
||||
|
|
|
1 |
3 = π . |
ка P находится в верхней полуплоскости, то можно взять x = arcctg |
||||
x1 |
|
|
1 |
6 |
Таким образом, на одном периоде решениями данного неравенства являются |
||||
π < x < π. Через период π значение котангенса повторяется. Таким образом, |
||||
6 |
|
|
|
|
все остальные решения данного неравенства получаем прибавлением к най |
||||
денным решениям чисел вида πk, где k Z. Ответ: 6π + πk < x < π + πk, k Z. |
||||
Аналогично предыдущим случаям при решении неравенства ctg x < |
3 с ис |
|||
пользованием графиков достаточно на одном периоде (например, на промежут |
||||
ке (0; π)) записать те абсциссы, для которых соответствующие точки графика |
||||
функции y = ctg x находятся ниже прямой y = |
3. (На рисунке в таблице 41 |
|||
соответствующие части графика функции y = ctg x выделены синими линиями.) |
||||
2. Способы решения более сложных тригонометрических неравенств так |
||||
же проиллюстрируем на примерах. |
|
|
|
|
Задача 5 |
|
|
Решите неравенство |
||||
|
|
|
|
|
Р е ш е н и е |
||
|
5 |
|
1 − cos2x |
+ |
1 |
(1− cos2 2x) < cos2x. |
|
|
|
|
|
||||
4 |
2 |
4 |
|
||||
Тогда 2 cos2 2x + 13 cos 2x – 7 > 0. Замена: cos 2x = t дает неравенство
5 sin2 x + 1 sin2 2x < cos 2x.
44
К о м м е н т а р и й
Используем равносильные преоб разования данного неравенства. Для этого приведем его к алгебраическому по схеме, аналогичной схеме решения
254

§ 22. Решение тригонометрических неравенств
2t2 + 13t – 7 > 0, решение которого: |
тригонометрических уравнений: |
||||||||||||||||||||
t < –7 или t > |
1 |
(см. рисунок). |
1) к одному аргументу (2x); |
||||||||||||||||||
|
2) к одной функции (cos 2x); |
||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) проведем замену переменной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(cos 2x = t). После обратной замены |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
решим полученные простейшие три |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратная замена дает: cos 2x < –7 (ре |
гонометрические неравенства. |
||||||||||||||||||||
|
|||||||||||||||||||||
шений нет) или cos 2x > |
1 |
. |
Тогда |
|
|||||||||||||||||
|
|
||||||||||||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
− |
π |
+ 2πn < 2x < |
π |
+ 2πn. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
3 |
|
|
|
|
|
|
|
3 |
|
|
|||||||||||
Таким образом, − |
π |
+ πn < x < |
π |
+ πn, |
|
||||||||||||||||
|
|
|
|||||||||||||||||||
66
n Z.
Решая более сложные тригонометрические неравенства, можно также при менить метод интервалов, немного изменив его. Необходимость коррекции известной схемы решения неравенств f (x) 0 методом интервалов (с. 232) связана с тем, что в случае, когда функция f (x) — тригонометрическая, она, как правило, имеет бесконечное множество нулей (которые получаются при целых значениях параметра). Поэтому, если пытаться обозначить нули на ОДЗ, придется обозначить бесконечное их множество, что невозможно. Избе жать этого можно, если найти период функции f (x) (если он существует) и рас смотреть знак функции на каждом промежутке внутри одного периода.
Таким образом, метод интервалов для решения тригонометрических не равенств f (x) 0 может применяться по схеме:
1.Найти ОДЗ неравенства.
2.Найти период функции f (x) (если он существует).
3.Найти нули функции (f (x) = 0).
4.Отметить нули на ОДЗ внутри одного периода и найти знак функции в каждом из промежутков, на которые разбивается ОДЗ (внутри одного периода).
5.Записать ответ (учитывая знак заданного неравенства и период функ ции f (x)).
Задача 6 Решите неравенство cos 2x m cos 3x – cos 4x.
Решим данное неравенство методом интервалов. Для этого приведем его к виду f (x) m 0:
1.ОДЗ: х — любое действительное число.
2.Как мы знаем, период функции cos х равен 2π. Тогда период функции cos 2x
будет T = |
2π |
= π, |
период функции cos 3x — T2 = |
2π |
, а период функции |
||
|
|||||||
1 |
2 |
|
|
|
3 |
|
|
cos 4x — T3 = |
2π |
= π . |
|||||
|
|||||||
|
4 |
|
2 |
|
|
||
255
РАЗДЕЛ 2. Тригонометрические уравнения и неравенства
На отрезке длиной 2π периоды Т1, Т2, Т3 помещаются целое число раз. Тогда 2π будет общим периодом для всех этих трех функций, и поэтому 2π является периодом функции f (x) = cos 2x + cos 4x – cos 3x.
3.Найдем нули этой функции: cos 2x + cos 4x – cos 3x = 0. Тогда 2 cos 3x cos x – cos 3x = 0, cos 3x (2 cos x – 1) = 0.
Отсюда cos 3x = 0 или 2 cos x – 1 = 0. Решая последние уравнения, получа
π+ πk , k Z, или x = ± π + 2πk, k Z.
6 |
3 |
3 |
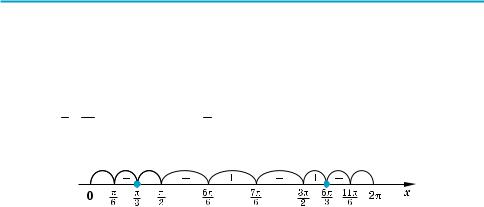
4.Отметим все нули на периоде длиной 2π, например на отрезке от 0 до 2π, и получим 9 промежутков (см. рисунок).
Находим знаки функции f (x) на каждом из промежутков. Для этого удоб но записать функцию f (x) в виде произведения: f (x) = cos 3x (2 cos x – 1).
Ответ (записывается с учетом периода):
|
π |
+ 2πk; |
π |
|
|
π |
+ 2πk; |
5π |
|
|
7π |
+ 2πk; |
3π |
|
|
|
|
|
x |
6 |
3 |
+ 2πk |
2 |
6 |
+ 2πk |
6 |
2 |
+ 2πk |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
5π |
+ 2πk; |
11π |
|
|
k Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
+ 2πk |
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
З а м е ч а н и е. При решении тригонометрических неравенств методом ин тервалов часто приходится находить знак функции в большом количестве промежутков. Для того чтобы уменьшить объем работы, можно предложить такой способ: следить за тем, через какой нуль мы проходим при переходе от одного интервала к другому и изменяется ли знак заданной функции в этом нуле.
В случае, когда функция f (x), которая стоит в левой части неравенства, записана в виде произведения ϕ (x) g (x), необходимо обращать внимание на то, что знак произведения не меняется, если одновременно оба множителя (функции ϕ (x) и g (x)) меняют знаки на противоположные.
Практически для использования этого свойства в случае, если левая часть неравенства записана как произведение нескольких функций, нули каждого множителя отмечают на промежутке разным цветом (так, как это сделано на рисунке к задаче 6), или, если множителей только два, нули первого множи теля обозначают под осью, а нули второго — над осью.
Если у функций множителей нет одинаковых нулей, то знак функции f (x) меняется автоматически при переходе через каждый нуль (при условии, что только одна из функций множителей меняет знак при переходе через этот нуль). В этом случае для нахождения всех знаков функции f (x) на периоде достаточно найти ее знак только в одном промежутке, а в других расставить знаки, чередуя их. Если же у функций множителей есть одинаковые нули, то при переходе через такой нуль знак произведения может не меняться, и это учитывается при расстановке знаков.
256

§ 22. Решение тригонометрических неравенств
Вопросы для контроля
1.Объясните на примерах, как можно решать простейшие тригонометриче ские неравенства с помощью: а) единичной окружности; б) графика соот ветствующей функции.
2.Всегда ли имеют решения неравенства: 1) sin x < a; 2) sin x > a; 3) cos x < a; 4) cos x > a; 5) tg x < a; 6) tg x > a; 7) ctg x < a; 8) ctg x > a? Могут ли быть решениями каких либо из этих неравенств все действительные числа? Приведите примеры.
3.Какими способами можно решать тригонометрические неравенства, кото рые отличаются от простейших ? Приведите примеры.
Упражнения
Решите неравенство (1–14).
1 |
. |
1) |
sin x m |
1 |
; |
|
|
|
|
|
|
2) sin x > − |
|
2 |
; |
3) sin x < –2; |
4) sin x l |
3 |
|
. |
|||||||||||||||||||
|
|
|
2 |
2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
. |
1) |
cos x > |
1 |
; |
|
|
|
|
|
|
2) cos x < − |
|
3 |
; |
3) cos x m 3; |
4) cos x l |
|
2 |
. |
|||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||
3 |
. 1) tg x < –1; |
2) tg x l |
3; |
|
|
|
3) |
tg x > |
3 |
; |
|
|
|
4) tg x m 1. |
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
4 |
. |
1) |
ctg x > − |
3; |
2) ctg x l 1; |
3) ctg x m –1; |
4) ctg x < |
3 |
. |
||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
5 |
. |
1) |
sin 2x > |
|
2 |
; |
2) cos |
x |
m |
|
3 |
; |
|
|
3) |
tg |
x |
l − 3; |
4) ctg 5x < 1. |
||||||||||||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
)< 3; |
|
|
|
|||||||
6 |
. |
1) |
2cos (2x − |
π |
)l1; |
|
|
|
|
|
|
2) |
3 tg (3x + |
π |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
2 sin ( |
|
|
|
3 |
|
|
|
)m1; |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|||||||||||||
|
|
3) |
|
x |
+ |
π |
|
|
|
|
|
|
4) |
2 cos (4x − 6π )> |
2. |
|
|
|
|
||||||||||||||||||||
|
|
3 |
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
7 |
. |
1) |
sin π cos 3x − cos π sin 3x > |
1 |
; 2) |
sin 5xcos 5x m |
1 |
; |
3) sin x + cos x < 1. |
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||||||
8 |
. |
1) |
|
sin(2x − π ) |
|
|
< 1 ; |
|
|
|
|
|
|
|
|
2) | tg x | > 1. |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
. |
1) |
sin 4x + cos 4x ctg 2x > 3; |
|
|
|
|
|
2) |
sin 4x − cos 4x tg 2x < 3. |
|
|
|
||||||||||||||||||||||||||
10. 1) sin x > cos2 x; |
|
|
|
|
|
|
2) cos2 x – sin2 x > sin 2x. |
|
|
|
|||||||||||||||||||||||||||||
11. 1) cos 2x + 5 cos x + 3 l 0; |
|
|
|
|
|
|
2) sin x < cos x. |
|
|
|
|
|
|||||||||||||||||||||||||||
12. 1) cos 2x + cos 6x > 1 + cos 8x; |
2) sin x sin 7x > sin 3x sin 5x. |
||||||||||||||||||||||||||||||||||||||
13. 1) |
|
sinx > |
− cosx; |
|
|
|
|
|
|
2) |
sinx > 1− sin2x. |
|
|
|
|||||||||||||||||||||||||
14.1) sin 9x – sin 5x + 2 sin2 x < 2 sin 2x + 1 – cos 2x; 2) 2 sin2 x – sin x + sin 3x < 1.
15.Найдите решения неравенства sin 2x < cosx − sinx, которые удовлетво ряют условию | x | < π.
257

РАЗДЕЛ 2. Тригонометрические уравнения и неравенства
16. Найдите значения х на отрезке 0 m x m π, которые удовлетворяют неравен ству sin 2x − cos x + 2 sin x l 1 .
|
2 |
17. Решите неравенство: |
2) a(cos x – sin x)2 + b cos2 x l 0. |
1) sin 4x > a(sin 3x – sin x); |
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К РАЗДЕЛУ 2
|
Решите уравнение (1–8). |
|
|
|
|
|
|
|||
1. |
1) sin2 x – 4 sin x = 5; |
2) cos2 x + 5 cos x = 6; |
||||||||
|
3) 4 cos2 x + 4 sin x – 1 = 0; |
4) 4 sin2 x – 4 cos x – 1 = 0. |
||||||||
2. |
1) sin 2x + tg x = 0; |
2) |
sin x + ctg |
x |
= 0; |
|
||||
|
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
3) |
2 sin2 x − 3 sin 2x = 0; |
4) |
2 cos2 x + 3 sin 2x = 0. |
||||||
3. |
1) |
1+ cosx − 2cos |
x |
= 0; |
2) |
1− cosx − 2 sin |
x |
= 0; |
||
|
|
|||||||||
|
|
2 |
|
|
2 |
|
||||
3)sinx − 3 cosx = 0;
4.1) cos2 x – 3 cos x sin x + 1 = 0;
3)2 + cos2 x = 2 sin x;
5.1) (1 + cos 4x) sin 2x = cos2 2x;
3)5 sin2 x + 4 sin (2π + x)= 4;
6. 1) 1− cos x − 3 sin x = 0;
2
4)3 sinx + cosx = 0.
2)sin2 x + 3 cos x sin x + 1 = 0;
4)3 – 3 cos x = 2 sin2 x.
2)(1 – cos 4x) cos 2x = sin2 2x;
4) 6 cos2 x + 5 cos (2π − x)= 7.
2) 1+ cos x + 3 cos x = 0;
2
|
3) cos2 4x + 3 sin2 2x – 1 = 0; |
4) cos2 4x + 3 cos2 2x – 1 = 0. |
||||||||||
7. |
1) |
cos 3x = 2 sin ( |
3 |
π + x); |
2) |
sin 3x = 2cos ( |
π |
− x); |
||||
|
|
|||||||||||
|
|
2 |
|
|
|
|
2 |
|
||||
|
3) |
1 – cos 4x = sin 2x; |
4) 1 + cos 4x = cos 2x. |
|||||||||
8. |
1) |
1− cos(π + x)− sin |
3π + x |
= 0; |
2) |
sin ( |
3 |
π − 2x)+ 5sin(π − x) + 3 = 0; |
||||
|
||||||||||||
|
|
2 |
|
|
2 |
|
|
|
||||
3)2 cos2 (2π + x)− 3 cos (2π − x)= 2; 4) 5 sin2 (1,5π – x) + 2 sin2 (π – x) = 2. Найдите решение уравнения (9–10).
9.1) sin x + cos x = 1 на интервале (–2π; 0);
2)sin x – cos x = 1 на интервале (0; 2π);
3)sin4 x – cos4 x = sin 2x на промежутке [0; 90°];
4)− sin2 x + cos2 x = cos x на промежутке [180°; 270°].
2
258

Дополнительные упражнения к разделу 2
10. 1) ctgx + |
|
sin x |
= 2 |
на интервале (π ; π); |
|
+ cosx |
|||
1 |
|
2 |
||
=sin x на промежутке [π; 2π];
1 + cos x 2
3)4 sin x sin 2x sin 3x = sin 4x на интервале (0; 2π );
4)4 cos x cos 2x sin 3x = sin 2х на интервале (0; 3π ).2) sin x
|
Решите уравнение (11–26). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
11. |
1) sin 6x – 2 sin 2x = 0; |
2) cos 6x + 2 cos 2x = 0; |
|
|
|
|||||||||||||||||||||
|
3) |
cos2 |
x |
+ cos 3x = sin2 |
x |
− cos x; |
4) sin2 x + sin 3x = cos2 x + sin x. |
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12. |
1) |
4 cos2 x – sin 2x = 1; |
2) |
3 sin2 x + |
1 |
sin 2x = 2; |
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3) sin2 x + 14 sin x cos x = 15 cos2 x; |
4) cos2 x – 12 cos x sin x = 13 sin2 |
||||||||||||||||||||||||
13. |
1) |
|
1 + cos 2x |
= 0; |
|
|
|
|
|
|
2) |
|
sinx − sin3x |
= 0; |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
1 − sin x |
|
|
|
|
|
|
|
1 − cos x |
|
|
|
|
|||||||||||
|
3) |
|
2sin2 x + 3sinx |
= 0; |
|
|
|
|
|
4) |
|
3cos2 x − 4cosx |
= 0. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 − cos x |
|
|
|
|
|
|
|
1 + sin x |
|
|
|
|
|||||||||||
14. |
1) |
|
cos x + cos 3x |
= 0; |
2) |
sinx − sin3x |
= |
0; |
3) |
|
cos 2x |
= 0; |
4) |
|
|
sin 2x |
||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
− sin 2x |
||||||||||||||||||
|
|
|
1 + sin x |
|
|
|
1 + cos x |
|
1 |
+ sin 2x |
|
|||||||||||||||
15. |
1) |
|
sin x + 3 cos x = 1; |
2) |
|
3 sin x − cos x = 1; |
|
|
|
|
||||||||||||||||
|
3) sin2 x = sin2 3x; |
|
|
|
|
|
4) cos2 x = cos2 3x. |
|
|
|
|
|||||||||||||||
x.
= 0.
16. |
1) |
|
sin 4x + sin 2x |
= tg 2x; |
2) |
|
cos 2x − sin 4x |
|
= ctg 2x; |
|||||
|
|
|
|
|
|
|||||||||
|
|
|
cos 2x |
|
|
sin 2x |
||||||||
|
3) |
|
1 + cosx = sin x; |
4) |
|
1− cosx = sin x. |
||||||||
17. |
1) |
sin4 x + cos4 x = |
5 |
; |
2) sin4 x + cos4 x = sin 2x; |
|||||||||
|
||||||||||||||
|
|
8 |
|
|
|
|
|
|
|
|||||
|
3) |
cos ( |
π |
+ 5x)+ sin x = 2cos 3x; |
4) |
cos 5x + sin ( |
3 |
π − 9x)− 3 sin 2x = 0. |
||||||
|
|
|
||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|||||
18.1) cos x + cos 2x + cos 3x + cos 4x = 0;
2)sin x + sin 2x + sin 3x + sin 4x = 0;
3)5 sin 2x – 11(sin x + cos x) + 7 = 0;
4)sin 2z + 5(sin z + cos z) + 1 = 0.
19.1) sin3 x cos 3x + cos3 x sin 3x + 0,375 = 0;
2) |
cos3 z cos 3z + sin3 z sin 3z = |
|
|
2 |
; |
|
|
|
|
||||||
4 |
|
|
|||||||||||||
|
|
|
|
|
|
|
4) 8cos x cos ( |
|
− x)cos ( |
|
+ x)+ 1 = 0. |
||||
3) |
sin xsin ( |
π |
− x)sin ( |
π |
+ x)= |
1 |
; |
π |
π |
||||||
|
3 |
||||||||||||||
|
|
|
|||||||||||||
|
3 |
|
3 |
|
8 |
|
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
20. 1) sin2 x + sin2 2x = sin2 3x; |
|
|
|
2) cos2 x + cos2 2x + cos2 3x + cos2 4x = 2; |
|||||||||||
3) |
cos 3x = 1 − |
3 sin 3x; |
|
|
|
4) 3 sin x + 5 cos x = 4. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
259 |
|
|
|
|
|
РАЗДЕЛ 2. Тригонометрические уравнения и неравенства
21. |
1) |
|
1+ 4sinxcosx = cosx − sinx; |
2) |
|
cos2x − sin4x = sinx − cosx; |
|||||||||||||||||
|
3) |
|
tg 4x |
+ |
tg |
2x |
+ |
5 |
= 0; |
4) |
|
ctg 2x |
+ |
|
ctg x |
+ 2 = 0. |
|||||||
|
|
|
|
|
|
|
|
|
|
ctg 2x |
|||||||||||||
|
|
|
tg 2x tg |
4x 2 |
|
|
ctg x |
|
|
|
|
|
|||||||||||
22. |
1) |
arcsin (x + 2,5) = |
π |
; |
2) |
arcsin |
( |
x |
− 3)= |
π |
; |
||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
6 |
|
|
|
|
|
|
2 |
|
6 |
|
|||||||
|
3) |
(x2 – 4) arcsin x = 0; |
4) |
(x2 − |
1 |
)arccosx = 0. |
|||||||||||||||||
|
4 |
||||||||||||||||||||||
23. 1) arccos (sinx) = x4 + 2π ;
3) arcsin (3 − 2x) = − π ;
4
24. 1) arcsin x arccos x = π2 ;
18
3)3 arcsin x – π = 0;
25.1) (arcsin x)2 – 4 arcsin x = 0;
3)arctg (1+ x)+ arctg (1− x) = π4 ;
26.1) tgx = −2sinx;
3)cosx = − sinx;
2) arctg (tgx)− x = π ;
4 2
4) arccos (2x − 3) = π3.
2) arctg x arcctg x = π2 ;
16
4) 4 arctg x − 6 (2π − arctg x)= π. 2) (arccos x)2 – 5 arccos x = 0;
4) arcsin (1 − x) − 2 arcsin x = π .
2
2)− tgx = 2 cosx;
4) cos2x = 2 sinx.
27. |
Найдите все значения х и у, удовлетворяющие уравнению: |
||||||||||||||||||||||||||||||
|
1) |
12 sin x + 5 cos x = 2y2 – 8y + 21; |
|
2) 3 cos x – 4 sin x = 2y2 – 4y + 7; |
|||||||||||||||||||||||||||
|
|
|
2tg |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 − tg2 |
x |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
3) |
|
|
|
2 |
|
|
|
= y2 − 4y + 5; |
4) |
|
|
2 |
|
= 2y2 − 4y + 3. |
||||||||||||||||
|
|
|
|
2 x |
|
|
|||||||||||||||||||||||||
|
|
1 + tg |
|
|
|
|
|
|
|
|
|
|
|
|
1 + tg2 |
x |
|||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Решите неравенство (28–36). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
28. |
1) |
cos2 x > |
1 |
; |
|
|
|
|
|
|
|
2) |
sin2 x < |
1 |
; |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
||||
|
3) |
2sin2 x + 3 sinx − 3 > 0; |
4) 2 sin2 x – 3 sin x + 1 l 0. |
||||||||||||||||||||||||||||
29. |
1) |
|
2cos2 x + cos x − 1 |
> 0; |
|
|
2) |
|
2sin2 x + sinx − 1 |
> 0; |
|
|
|||||||||||||||||||
|
|
|
cos x − 1 |
|
|
|
|
|
|
|
sin x − 1 |
||||||||||||||||||||
|
3) |
cos3 xcos 3x − sin3 xsin 3x > |
5 |
; |
4) |
cos3 x sin 3x + cos 3x sin3 x < |
3 |
. |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
8 |
|
|||||||||||
30. |
1) |
sin4 |
x |
+ cos4 |
x |
> |
1 |
; |
2) |
sin6 x + cos6 x > |
5 |
; |
|||||||||||||||||||
|
|
3 |
|
|
|
3 |
|
2 |
|
|
|
|
|
|
8 |
|
|
|
|||||||||||||
|
3) |
sinx + |
|
3 cosx > 1; |
4) |
|
3 sin3x + cos3x > 1. |
||||||||||||||||||||||||
260
Дополнительные упражнения к разделу 2
31. |
1) |
tg2 x + (2 − |
3)tg x − 2 3 < 0; |
2) |
3 tg2 x − 4tgx + 3 > 0; |
|
||||||||||||||||||||||
|
3) ctg2 x + ctg x l 0; |
|
|
|
4) tg2 x – tg x m 0. |
|
||||||||||||||||||||||
32. |
1) tg x tg 3x < –1; |
|
|
|
2) ctg x ctg 3x > –1; |
|
||||||||||||||||||||||
|
3) |
3 sin2 x – 2 sin x cos x – cos2 x m 0; |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
4) |
2cos |
2 |
x + |
( |
2 |
|
|
|
|
) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
3 − 1 cos x sin x − 3 sin x l 0. |
|
||||||||||||||||||||||
|
|
|
sin 3x cos(2x − |
π |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
33. |
1) |
|
|
|
|
|
|
|
|
6 |
|
|
m0; |
|
|
|
2) cos x cos 2x cos 3x m 0; |
|
||||||||||
|
|
|
sin 2x |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3) |
(3 2 cos x − |
|
2 sin x − 2 − 3 )(2sin 2x − 1)l0; |
|
|||||||||||||||||||||||
|
4) |
cos2x + 2sin2x 2 |
2 cosx; |
|
|
|
|
|
|
|
|
|
||||||||||||||||
34. |
1) |
3 sin 2x – 1 > sin x + cos x; |
2) cos 2x m 2 (cos x − sin x); |
|
||||||||||||||||||||||||
|
3) |
|
1 |
|
|
+ |
|
1 |
+ |
|
|
1 |
|
< 0; |
|
|
4) |
1 |
− |
1 |
l |
1 |
. |
|
|
|||
|
|
sin2x |
sin 4x |
sin8x |
sinx |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
sin2x sin3x |
|
||||||||||||||||
35. |
1) |
2 arccos x > arcsin x; |
2) 2 arcsin x > arccos x; |
|
||||||||||||||||||||||||
|
3) |
2 (arcsin x)2 – 3 arcsin x + 1 > 0; |
4) (arccos x)2 – 6 arccos x + 8 < 0. |
|||||||||||||||||||||||||
36. |
1) sin (2x + 10°) + sin (x + 10°) – sin x < 0; |
|
|
|
|
|
|
|
||||||||||||||||||||
|
2) |
ctg x + ctg (x + |
π |
)+ 2 ctg (x + |
π |
)> 0; |
|
3) |
(arctg x)3 + (arcctg x)3 > |
π3 |
; |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
32 |
|
||||||||
4) arctg (3x2 – 3x + 1) < arcctg (3x2 – 3x + 1).
37.Найдите множество значений функции:
|
y = |
3 |
arccos ( 0,125 |
(cos x − sin x)); |
|
y = |
9 |
|
3 |
2 + sinx − cosx |
|
1) |
2) |
arcsin |
. |
||||||||
|
|
π |
|
|
|
π |
|
|
4 2 |
|
|
38. Найдите множество значений функции y = sin 2x, если:
1) х [arctg 0,5; arctg 3]; |
2) |
x [arctg |
1 |
;arctg 2]; |
|||||||
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
3) x arccos 0,8; |
5π |
; |
4) |
x arccos |
5 |
; |
5π |
. |
|||
|
12 |
|
|
|
13 |
|
12 |
|
|||
39. Решите уравнение: |
|
|
|
|
|
|
|
|
|
||
1) 7 tg x + cos2 x + 3 sin 2x = 1; |
2) sin 2x + 1 = sin2 x + 6 ctg x. |
||||||||||
40.При каких значениях а выражение 2 + cos x (5 cos x + a sin x) будет рав няться единице хотя бы при одном значении х?
41.При каких значениях а выражение 3 + sin x (2 sin x + a cos x) будет рав няться (–1) хотя бы при одном значении х?
261
