
Algebra_10kl_RU
.pdf
РАЗДЕЛ 4. Показательная и логарифмическая функции
Примеры решения задач
Задача 1 |
Вычислите: 1) log5 125; |
Ре ш е н и е
1)log5 125 = 3, поскольку 53 = 125;
2)log 1 3 = − 1 , так как
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
)− |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
3 = |
1 |
= |
|
1 |
= |
1 |
= 3. |
|||||
|
1 |
3 |
1 |
1 |
|||||||||
27 |
|
( |
1 |
)3 |
|
3 |
|
||||||
|
|
|
|
|
|
27 |
|
||||||
|
|
|
|
27 |
|
|
|
|
|
|
|
||
2) log 1 3.
27
К о м м е н т а р и й Учитывая определение логариф%
ма, необходимо подобрать такой по% казатель степени, чтобы при возведе% нии основания логарифма в эту сте% пень получить число, стоящее под знаком логарифма.
Задача 2 |
Запишите решение простейшего показательного уравнения: |
|||||||
|
1) 5х = 3; |
2) |
( |
1 |
)x = 10; |
3) 10x = |
1 |
. |
|
||||||||
|
|
|
||||||
|
|
|
3 |
|
3 |
|
||
Р е ш е н и е По определению логарифма:
1)х = log5 3;
2)x = log1 10;
3
3)x = lg 1.
3
К о м м е н т а р и й
Для любых положительных чисел b и а (а ≠ 1) уравнение ах = b имеет единственный корень. Показатель степени х, в которую необходимо воз% вести основание а, чтобы получить b, называется логарифмом b по основа% нию а, поэтому х = logа b.
27a2
Задача 3 Выразите логарифм по основанию 3 выражения 5 b (где a > 0 и
b > 0) через логарифмы по основанию 3 чисел a и b. (Коротко говорят так: «Прологарифмируйте заданное выражение по ос" нованию 3».)
Р е ш е н и е
log3 |
27a2 |
= log3 |
33a2 |
= |
|
1 |
|||
|
5 b |
|
||
|
|
|
b5 |
|
1
= log3 (33a2 ) − log3 b5 =
1
= log3 (33 ) + log3 a2 − log3 b5 =
= 3log3 3 + 2log3 a − 1 log3 b =
5
= 3 + 2log3 a − 1 log3 b.
5
К о м м е н т а р и й
Сначала запишем выражения, стоящие в числителе и знаменателе данного выражения, как степени чи% сел и букв. Далее учтем, что логарифм
частного |
33a2 |
положительных чисел |
|
1 |
|||
|
|
||
|
b5 |
|
равен разности логарифмов числите% ля и знаменателя, а затем то, что ло% гарифм произведения (33а2) равен сумме логарифмов множителей.
362

§ 31. Логарифм числа. Свойства логарифмов
После этого учтем, что каждый
1
из логарифмов степеней (33; a2; b5 )
равен произведению показателя сте% пени на логарифм основания этой сте% пени, а также то, что log3 3 = 1.
Задача 4 Известно, что log2 5 = a, log2 7 = b. Выразите log2 700 через a и b.
Р е ш е н и е log2 700 = log2 (7æ52æ22) =
=log2 7 + log2 52 + log2 22 =
=log2 7 + 2 log2 5 + 2 log2 2 =
=b + 2a + 2.
К о м м е н т а р и й Сначала представим число 700 как
произведение степеней данных чисел 5 и 7 и основания логарифма 2, а да% лее используем свойства логарифмов и подставим в полученное выражение значения log2 5 и log2 7.
|
|
ab3 |
||
|
|
|||
Задача 5* |
Прологарифмируйте по основанию 10 выражение |
|
|
. |
c |
2 |
|||
|
|
|
|
|
|
|
Р е ш е н и е |
|
Если |
ab3 |
> 0, то |
|
c2 |
|||
|
|
3
lg ab2 = lg ab3 − lg c2 =
c
=lg (| a |æ| b3 |) – lg | c |2 =
=lg | a | + lg | b3 | – 2 lg | c | =
=lg | a | + 3lg | b | – 2lg | c |.
К о м м е н т а р и й
Поскольку логарифмы существу% ют только для положительных чи% сел, то мы можем прологарифмиро% вать данное выражение только в слу%
чае, когда |
ab3 |
> 0. |
|
c2 |
|||
|
|
Из условия не следует, что в данном выражении значения a, b, c положи% тельны. Поэтому будем пользоваться обобщенными формулами логариф% мирования (2R–4R), а также учтем, что | ab3 | = | a |æ| b3 |, | b3 | = | b |3, | c2 | = | c |2.
Иногда приходится искать выражение, зная его логарифм. Такую опера% цию называют потенцированием.
Задача 6 Найдите x по его логарифму:
1) lg x = lg 5 – 2lg 3 + 3lg 2; 2) loga x = 1 loga b + 5loga c − loga p.
2
Ре ш е н и е
1)lg x = lg 5 – 2lg 3 + 3 lg 2, lg x = lg 5 – lg 32 + lg 23,
lg x = lg |
5 23 |
x = |
5 |
23 |
= |
40 |
|
|
|
, |
|
|
|
; |
|||
2 |
3 |
2 |
9 |
|||||
|
3 |
|
|
|
|
|
||
К о м м е н т а р и й
Пользуясь формулами логариф% мирования справа налево, запишем правые части данных равенств в виде логарифма какого%то выражения.
363

РАЗДЕЛ 4. Показательная и логарифмическая функции
2) loga x = 1 loga b + 5loga c − loga p,
2
1
loga x = loga b2 + loga c5 − loga p,
|
|
1 |
5 |
|
|
1 |
|
5 |
|
|
|
b |
2 |
|
b |
2 |
c |
|
|||
loga x = loga |
|
c |
, |
x = |
|
|
. |
|||
|
p |
|
p |
|
||||||
|
|
|
|
|
|
|
||||
Из полученного равенства
logа x = logа M (1) получаем x = M
(как будет показано в § 32, значе% ние x, удовлетворяющее равенству (1), — единственное).
|
|
|
4 |
|
+ 1 log 4 |
||
Задача 7 |
* |
Вычислите значение выражения 5 |
log |
3 5 |
2 |
5 |
. |
|
|||||||
|
|
|
|
|
|||
Р е ш е н и е
|
Поскольку log 3 5 = |
|
log5 5 |
= |
|
|
|
|
|
|
|||||||||||||||||||
|
|
log5 |
3 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
1 |
|
= |
|
2 |
|
|
, то |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 log |
3 |
log |
5 |
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
5 |
|
|
|
|
|
|
|
|
|
||||
4 |
= |
|
|
4 |
|
|
= 2log5 |
3 = log5 32 = log5 9. |
|||||||||||||||||||||
|
log 3 5 |
|
|
2 |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
log5 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Кроме того, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 log5 4 = log5 42 = log5 |
4 = log5 2. |
|
||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
4 |
|
|
+ |
1 |
log |
|
4 = log 9 + log |
|
|
2 |
= |
|||||||||||||||||
|
|
|
|
5 |
5 |
||||||||||||||||||||||||
|
|
|
log |
3 5 |
2 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
= log |
5 |
(9 2) = log 18. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|||
|
|
|
|
4 |
|
+ 1 log 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Итак, 5 |
log |
3 5 |
|
2 |
5 |
= |
5 |
log5 18 |
= 18. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
К о м м е н т а р и й
Попытаемся привести показатель степени данного выражения к виду log5 b, чтобы можно было воспользо% ваться основным логарифмическим
тождеством:
5log5 b = b.
Для этого перейдем в показателе сте% пени к одному основанию логарифма (к основанию 5).
Вопросы для контроля
1.Дайте определение логарифма положительного числа b по основанию а (а > 0, а ≠ 1).
2.Какой логарифм называют десятичным логарифмом и какой натуральным логарифмом? Приведите примеры записи и вычисления таких логарифмов.
3.1) Запишите основное логарифмическое тождество. Приведите примеры его использования. 2*) Обоснуйте основное логарифмическое тождество.
4.1) Запишите и сформулируйте формулы логарифмирования. Приведите примеры их использования. 2*) Обоснуйте формулы логарифмирования.
5.1) Запишите формулу перехода от одного основания логарифма к другому. Приведите примеры ее использования. 2*) Обоснуйте формулу перехода от одного основания логарифма к другому.
6*. Можно ли в том случае, когда значение x и y оба отрицательные, пролога% рифмировать выражение: xy, xy, x4? Как это сделать? Обоснуйте соответ% ствующие формулы.
364

§ 31. Логарифм числа. Свойства логарифмов
|
Упражнения |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1°. Проверьте, верно ли равенство: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
1) log2 16 = 4; |
|
|
|
2) log3 27 = 3; |
|
|
|
3) log2 |
1 |
= −2; |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||
|
4) log 2 4 = 4; |
|
|
|
5) log1 8 = −3; |
|
|
|
6) log0,2 0,008 = 3. |
|
|
||||||||||||||||
2. Вычислите: |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1°) log |
|
|
25; |
2°) log |
|
64; |
3°) log |
|
1 |
; |
4°) |
log |
|
6; |
5) log |
|
|
1 |
; |
|
6°) log |
|
1; |
|||
|
5 |
4 |
3 |
9 |
6 |
9 |
27 |
|
1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7*) log |
2 |
4 23 |
2; |
8*) log |
5 74 7; 9*) log |
(7 − 4 3 ); 10*) log |
|
(9 + 4 |
5 ). |
|||||||||||||||||
|
|
|
|
|
|
|
7 |
|
|
|
|
|
7+ 4 3 |
|
|
|
|
|
|
|
|
9−4 5 |
|
|
|||
3°. Пользуясь определением логарифма, запишите решение простейшого по% казательного уравнения:
1) 4х = 9; 2) (14 )x = 15; 3) 10х = 11; 4) 5х = 19; 5) 0,2х = 0,7; 6) ех = 3 .
4. Пользуясь основным логарифмическим тождеством, упростите выражение:
|
|
log |
1 |
|
|
|
log1 |
6 − 2 |
|
1) 5log57; 2) 3log34; |
3) |
3 3 |
|
4) 3,5log3,5 13; 5*) 71+log7 2; 6*) ( |
1 |
) 3 |
. |
||
3 |
; |
||||||||
|
|||||||||
|
|
|
|
|
3 |
|
|
||
5.Прологарифмируйте данное выражение по заданному основанию, зная, что а > 0, b > 0, c > 0:
1°) 10а3с4 по основанию 10; |
|
|
0,1a2b5 |
|||||
2) |
|
|
|
|
по основанию 10; |
|||
c7 |
|
|||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
2 |
|
|
3°) a2c |
|
b по основанию е; |
4) |
|
a2b3 |
по основанию е; |
||
|
|
c2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
5°) 9a7 |
3 |
b по основанию 3; |
6) |
|
a5b4 |
по основанию 3. |
||
|
|
1 |
|
|||||
|
|
|
|
|
c2 |
|
|
|
6*. Прологарифмируйте данное выражение по основанию 10, зная, что аb > 0 и с ≠ 0:
|
|
|
|
|
|
|
|
|
|
3 ab |
|
|
|
|
c4 |
|
; |
|
|
|
|
|
5 |
|
|
|
||||
|
1) а3b5с8; |
|
|
2) |
|
|
|
; |
|
3) |
|
|
|
|
|
|
|
|
4) 100 |
|
abc2 . |
|
|
|||||||
|
|
|
c2 |
|
|
(ab) |
2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||
7. |
Известно, что log5 2 = a, log5 3 = b. Выразите через a и b: |
|
|
|
|
|||||||||||||||||||||||||
|
1) log5 15; |
|
|
2) log5 12; |
3) log5 30; |
|
|
|
4) log5 72. |
|
|
|||||||||||||||||||
8. |
Найдите х, если: |
|
|
|
|
|
|
|
|
|
|
|
|
|
lgx = |
1 |
lg(5a) − 2lgb + 5lgc; |
|||||||||||||
|
1) log |
|
|
x = 3 log |
|
2 + 0,5 log |
|
25 – 2 log |
|
3; |
2) |
|||||||||||||||||||
|
6 |
6 |
6 |
6 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
|
3) lgx = 3lgm + |
2 |
lgn − |
1 |
lg p; |
|
4) log3 x = |
1 |
log3 8 − 2log3 20 − 3log3 2. |
|
|
|||||||||||||||||||
|
|
|
|
3 |
|
|
||||||||||||||||||||||||
9. |
|
|
|
|
|
7 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Замените данный логарифм логарифмом по основанию 3: |
|
|
|
|
||||||||||||||||||||||||||
|
1) log |
1 |
a; |
2) log |
9 |
a; |
|
3) log |
1 |
a; |
|
|
4) log |
3 |
a; |
|
5) log |
2 |
a. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
365
|
|
|
РАЗДЕЛ 4. Показательная и логарифмическая функции |
|||||||||||
10*. Вычислите значение выражения: |
|
|
|
|||||||||||
|
|
6 |
+ 1 log627 |
|
|
|
2 |
|
+ 1 log316 |
|
|
|
||
1) |
6 |
log 2 6 |
3 |
|
; |
2) 3 |
log 5 3 |
|
4 |
; |
|
|
||
|
|
|
|
|
|
|
|
|
||||||
3) log4 5ælog5 6ælog6 7ælog7 32; |
4) log9 10ælg 11ælog11 12ælog12 27; |
|||||||||||||
|
|
1 |
1 |
4 + 25log125 8 ) |
49log7 2; |
6) 15 log1 (5 |
4 |
49 ). |
||||||
5) |
(814 − |
2 log9 |
7 1 5log 5 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
7 |
49 |
|
11*. 1) |
Найдите log |
8 |
9, если log |
12 |
18 = a; |
|
|
|||||||
2) |
Найдите log9 15, если log45 25 = a; |
|
|
|||||||||||
3) |
Найдите log175 56, если log14 7 = a и log5 14 = b; |
|
||||||||||||
4) |
Найдите log150 200, если log20 50 = a и log3 20 = b. |
|
||||||||||||
§32 |
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, |
|
||||||||||||
|
|
|
ЕЕ СВОЙСТВА И ГРАФИК |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т а б л и ц а 54 |
О п р е д е л е н и е. Логарифмической функцией называется функция |
||||||||||||||
|
|
|
|
|
|
вида у = loga х, где а > 0, а ≠ 1. |
|
|||||||
|
|
|
|
|
|
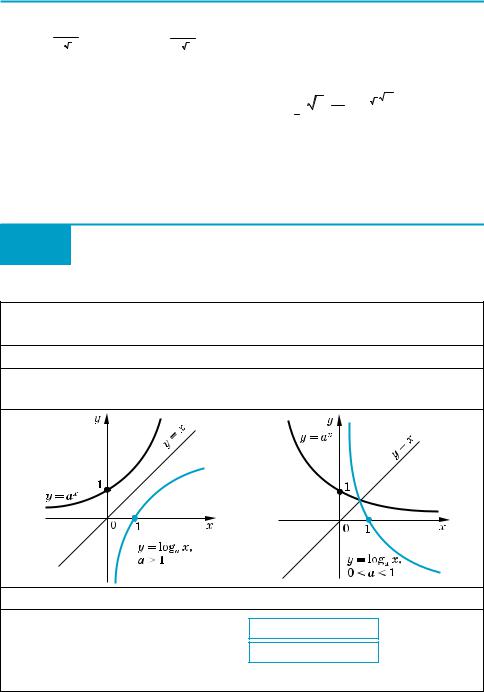
1. График логарифмической функции |
|
|||||||
Функции у = аx и у = log |
a |
х (а > 0, а ≠ 1) — взаимно обратные функции, |
||||||||||||
поэтому их графики симметричны относительно прямой у = х. |
||||||||||||||
|
|
|
|
|
2. Свойства логарифмической функции |
|
||||||||
1. Область определения: x > 0. |
D (loga x) = (0; +×) |
|
||||||||||||
2. Область значений: y R. |
E (loga x) = R |
|
||||||||||||
3. Функция ни четная, ни нечетная. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
366 |
|
|
|

§32. Логарифмическая функция, ее свойства и график
Пр о д о л ж. т а б л. 54
4.Точки пересечения с осями координат:
|
|
|
y = 0, |
с осью Oy |
нет |
с осью Ox |
|
|
|
|
x = 1 |
|
|
|
5. |
Промежутки возрастания и убывания: |
||||||||||
|
|
|
|
|
|
|
|
||||
|
|
а > 1 |
|
|
0 < а < 1 |
||||||
функция loga х возрастает при а > 1 |
функция loga х убывает при 0 < а < 1 |
||||||||||
|
на всей области определения |
|
на всей области определения |
||||||||
|
|
|
|
|
|
|
|||||
6. |
Промежутки знакопостоянства: |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||
|
|
а > 1 |
|
|
0 < а < 1 |
||||||
|
|
|
|
|
|
|
|
||||
|
у = loga х > 0 при х > 1, |
|
|
у = loga х > 0 при 0 < х < 1, |
|||||||
|
у = loga х < 0 при 0 < х < 1 |
|
у = loga х < 0 при х > 1 |
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
||||||||
7. |
Наибольшего и наименьшего значений функция не имеет. |
|
|||||||||
|
|
|
|
|
|
|
|
||||
8. |
|
loga a = 1 |
|
|
|
|
|
||||
|
|
loga (uv) = loga u + loga v |
(u > 0, v > 0) |
|
|||||||
|
|
loga |
u |
= loga u − loga v (u > 0, v > 0) |
|
||||||
|
|
||||||||||
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
log |
a |
uп = п log |
u (u > 0) |
|
|
|
|||
|
|
|
|
|
a |
|
|
|
|
|
|
Объяснение и обоснование
1. Понятие логарифмической функции и ее график. Логарифмической функ" цией называется функция вида у = loga х, где а > 0, а ≠ 1.
Покажем, что эта функция является обратной к функции у = аx.
(Действительно, показательная функция f (х) = аx при а > 1 возрастает на
множестве R, а при 0 < а < 1 — убывает на множестве R. Область значений функции f (х) = аx — промежуток (0; +×). Таким образом, функция f (х) обратима (с. 141) и имеет обратную функцию с областью определения (0; +×) и областью значений R. Напомним, что для записи формулы обратной функ% ции достаточно из равенства у = f (х) выразить х через у и в полученной
формуле х = g (у) аргумент обозначить через х, а функцию — через у. Тогда из уравнения у = аx (а > 0, а ≠ 1) по определению логарифма получаем
х = loga у — формулу обратной функции, в которой аргумент обозначен через у, а функция — через х. Изменяя обозначения на традиционные, имеем формулу у = loga х — функции, обратной к функции у = аx. )
367

РАЗДЕЛ 4. Показательная и логарифмическая функции
а |
б |
Рис. 127 |
Как известно, графики взаимно обратных функций симметричны относи% тельно прямой у = х. Таким образом, график функции у = loga х (а > 0, а ≠ 1) можно получить из графика функции у = ах симметричным отображением относительно прямой у = х. На рисунке 127 приведены графики логарифмиче% ских функций при а > 1 и при 0 < а < 1. График логарифмической функции называют логарифмической кривой.
2. Свойства логарифмической функции. Свойства логарифмической функ% ции, указанные в пункте 8 таблицы 54, были обоснованы в § 31. Другие свой% ства функции у = loga х прочитаем из полученного графика этой функции или обоснуем, опираясь на свойства функции у = ах.
Поскольку область определения прямой функции является областью зна% чений обратной, а область значений прямой функции — областью определе% ния обратной, то, зная эти характеристики для функции у = ах, получаем соответствующие характеристики для функции y = loga x:
Характеристика |
|
Функция |
|
|
|
|
|
y = ax |
|
y = log x |
|
|
|
||
|
|
|
a |
Область определения |
R |
|
(0; ×) |
|
|
|
|
Область значений |
(0; ×) |
|
R |
1)Областью определения функции у = loga х является множество R+ всех положительных чисел (х > 0);
2)Областью значений функции у = loga х является множество R всех дей" ствительных чисел (тогда функция y = loga x не имеет ни наибольшего, ни наименьшего значений).
3)Функция у = loga х не может быть ни четной, ни нечетной, поскольку ее область определения не симметрична относительно точки 0.
4) График функции у = loga х не пересекает ось Oу, поскольку на оси Oу х = 0, а это значение не принадлежит области определения функции у = loga х.
368

§ 32. Логарифмическая функция, ее свойства и график
График функции у = loga х пересекает ось Oх в точке х = 1, поскольку loga 1 = 0 при всех значениях а (а > 0, а ≠ 1).
5) Из графиков функции у = loga х, приведенных на рисунке 127, видно, что
при а > 1 функция у = loga х возрастает на всей области определе ния, а при 0 < а < 1 — убывает на всей области определения.
(Это свойство можно обосновать, опираясь не на вид графика, а только на свойства функции у = аx.
Например, при а > 1 возьмем x2 > x1 > 0. По основному логарифмическому
тождеству можно записать: x1 = aloga x1, x2 = aloga x2. Тогда, учитывая, что
х2 > х1, имеем aloga x2 > aloga x1. Поскольку при а > 1 функция у = аx является возрастающей, то из последнего неравенства получаем loga x2 > loga x1. А это и означает, что при а > 1 функция у = loga х возрастает на всей обла% сти определения.
Аналогично можно обосновать, что при 0 < а < 1 функция у = loga х убыва% ет на всей области определения. )
6)Промежутки знакопостоянства. Поскольку график функции у = loga х
пересекает ось Oх в точке х = 1, то, учитывая возрастание функции при а > 1 и убывание при 0 < а < 1, имеем:
|
Значение функции |
|
|
Значение аргумента |
|
|
|||
|
|
|
|
|
|
|
|
||
|
при a > 1 |
|
при 0 < a < 1 |
|
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
y > 0 |
x (1; +×) |
|
x (0; 1) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
y < 0 |
|
x (0; 1) |
|
x (1; +×) |
|
||
|
Примеры решения задач |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 1 |
Найдите область определения функции: |
|
|
|
|||||
|
|
1) у = log |
(3 – х); |
|
2) y = log1 (x2 + 3); |
3) у = log |
(х2 |
– х). |
|
|
|
5 |
|
3 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||
Ре ш е н и е
1)Область определения функции
у = log5 (3 – х) задается неравенством 3 – x > 0. Отсюда x < 3. То есть
D(y) = (–×; 3).
2)Область определения функции
y = log1 (x2 + 3) задается неравенст%
3
вом x2 + 3 > 0. Это неравенство выпол% няется при всех действительных зна% чениях х. Таким образом, D (y) = R.
К о м м е н т а р и й Поскольку выражение, стоящее
под знаком логарифма, должно быть положительным, то для нахождения области определения заданной функ% ции необходимо найти те значения аргумента х, при которых выраже% ние, стоящее под знаком логарифма, будет положительным.
369

РАЗДЕЛ 4. Показательная и логарифмическая функции
3)Область определения функции
у= log7 (х2 – х) задается неравен% ством х2 – х > 0. Решая это квад% ратное неравенство, получаем x < 0 или x > 1 (см. рисунок).
То есть D (y) = (–×; 0) (1; +×).
Задача 2 Изобразите схематически график функции:
|
|
|
|
|
|
|
|
|
|
|
1) у = log2 х; |
2) y = log1 x. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1) у = log2 х |
Р е ш е н и е |
|
|
К о м м е н т а р и й |
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Область определения функции |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
у = logа х — значения х > 0, следова% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельно, график этой функции всегда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расположен справа от оси Оу. Этот |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
график пересекает ось Ох в точке |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х = 1 (logа 1 = 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При а > 1 логарифмическая функ% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ция возрастает, таким образом, гра% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фиком функции у = log2 х будет лога% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
x |
|
1 |
|
|
|
2 |
|
|
4 |
|
рифмическая кривая, точки которой |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при увеличении аргумента поднима% |
|||
y |
|
0 |
|
|
|
–1 |
1 |
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
ются. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При 0 < а < 1 логарифмическая |
2) |
y = log1 x |
|
|
|
|
|
|
|
|
|
|
|
|
функция убывает, таким образом, |
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
графиком функции y = log1 x будет |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
логарифмическая кривая, точки ко% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
торой при увеличении аргумента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
опускаются. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы уточнить поведение графи% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ков данных функций, найдем коор% |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
динаты нескольких дополнительных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точек. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
1 |
|
|
|
|
1 |
2 |
|
|
4 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y |
|
0 |
|
|
|
1 |
|
|
|
–1 |
–2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
370

§ 32. Логарифмическая функция, ее свойства и график
Задача 3*. Изобразите схематически график функции у = lоg3 | x – 2 |.
Р е ш е н и е Последовательно строим графи%
ки:
1.y = lоg3 x;
2.y = lоg3 | x |;
3.y = lоg3 | x – 2 |.
К о м м е н т а р и й
Составим план последовательно% го построения графика данной функ% ции с помощью геометрических пре% образований (см. табл. 4, с. 28).
1.Мы можем построить график функ%
ции y = f (x) = lоg3 x (основание ло% гарифма а = 3 > 1 — логарифми% ческая функция возрастает).
2.Затем можно построить график функции
y = g (x) = lоg3 | x |= f (| x |) (справа от оси Oy график функции
f (x) остается без изменений, и эта же часть графика симметрично отображается относительно оси Oy).
3.После этого можно построить гра% фик заданной функции
y = lоg3 | x – 2 | = g (x – 2) параллельным переносом графика
функции g (x) вдоль оси Ox на 2 единицы.
Задача 4 |
Сравните положительные числа b и c, зная, что: |
|
|
||||
|
|
1) log3 b > log3 c; |
2) log0,3 b > log0,3 c . |
|
|
||
|
|
Р е ш е н и е |
|
К о м м е н т а р и й |
|
|
|
|
|
|
|
|
|||
1) |
Поскольку функция у = log3 х |
В каждом задании данные выра% |
|||||
|
является возрастающей, то для |
жения — это значения логарифмичес% |
|||||
|
положительных чисел b и c из не% |
кой функции у = logа х в точках b и c. |
|||||
|
равенства log3 b > log3 c получаем |
Используем возрастание или убы% |
|||||
|
вание соответствующей функции: |
|
|||||
|
|
b > c. |
|
|
|||
|
|
|
1) при а = 3 > 1 функция у = log3 х |
||||
2) |
Поскольку функция у = log0,3 х |
||||||
возрастающая, и поэтому больше% |
|||||||
|
является убывающей, то для по% |
||||||
|
му значению функции соответст% |
||||||
|
ложительных чисел b и c из нера% |
||||||
|
вует большее значение аргумента; |
||||||
|
венства log0,3 b > log0,3 c получаем |
||||||
|
2) при а = 0,3 < 1 функция у = log |
0,3 |
х |
||||
|
|
b < c. |
|
|
|
||
|
|
|
убывающая, и поэтому большему |
||||
|
|
|
|
значению функции соответствует |
|||
|
|
|
|
меньшее значение аргумента. |
|
|
|
|
|
|
|
|
|
|
|
371
