Algebra_10kl_RU

РАЗДЕЛ 4. Показательная и логарифмическая функции

382

§ 33. Решение логарифмических уравнений и неравенств

log2 x + log2 y = 2, Задача 6 Решите систему уравнений ( )

log3 y − x = 1.

383

РАЗДЕЛ 4. Показательная и логарифмическая функции

З а м е ч а н и е. Данную систему можно было решить и с помощью равно% сильных преобразований систем. При этом пришлось бы учесть ОДЗ данной

ний (в данном случае все написанные преобразования являются равносиль% ными на ОДЗ), а в конце проверить, удовлетворяют ли полученные решения

не удовлетворяет условиям ОДЗ).

logy x + logx y = 2,

Задача 7 Решите систему уравнений 2 − =

x y 20.

384

§ 33. Решение логарифмических уравнений и неравенств

Вопросы для контроля

1. Объясните на примерах, как можно решать простейшие логарифмические уравнения, используя определение логарифма.

2*. Обоснуйте справедливость равносильного перехода: loga f (x) = c f (x) = ac (а > 0, а ≠ 1).

3.Объясните, как можно решить уравнение log5 (x – 2) = log5 (x2 – 2): а) с помощью уравнений%следствий; б*) с помощью равносильных преобразований.

4.Объясните на примере применение замены переменных при решении лога% рифмических уравнений. В каких случаях целесобразно применять замену переменных?

Упражнения

Проверьте подстановкой, что найденое значение x действительно явля% ется корнем уравнения.

7*. Докажите, что уравнения, приведенные в задании 6, не имеют других кор% ней, кроме найденных графически.

8. Решите системy уравнений:

385

РАЗДЕЛ 4. Показательная и логарифмическая функции

33.2. РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ

Т а б л и ц а 56

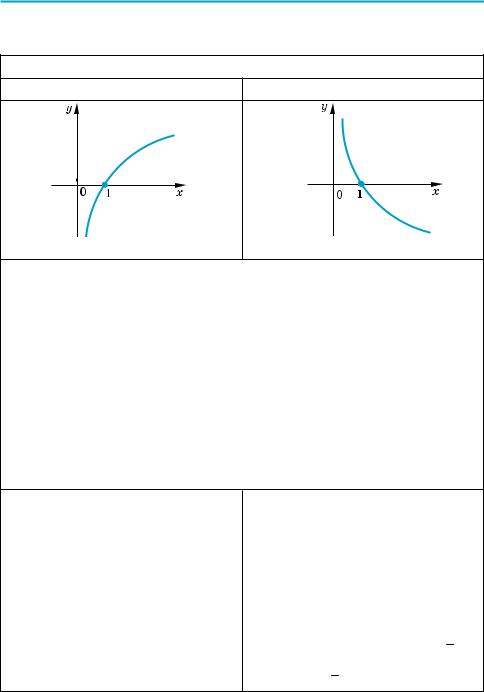
1. График функции y = loga x (a > 0; a ≠ 1)

2. Равносильные преобразования простейших логарифмических неравенств

Примеры

386

§33. Решение логарифмических уравнений и неравенств

Пр о д о л ж. т а б л. 56

3.Решение более сложных логарифмических неравенств

387

РАЗДЕЛ 4. Показательная и логарифмическая функции

Объяснение и обоснование

1.Решение простейших логарифмических неравенств. Простейшими ло" гарифмическими неравенствами обычно считают неравенства вида

( Для решения такого неравенства можно применять равносильные преоб%

f (x) > 0,

разования. Для этого необходимо учесть его ОДЗ: g (x) > 0 и рассмотреть

два случая: основание логарифма больше 1 и основание меньше 1 (но боль% ше 0).

І.При a > 1 логарифмическая функция y = loga t возрастает на всей своей области определения (то есть при t > 0), и поэтому большему значению функции соответствует большее значение аргумента. Таким образом, пе% реходя в неравенстве (1) от значений функции к значениям аргумента (в данном случае переходя к выражениям, стоящим под знаком логариф% ма), мы должны оставить тот же знак неравенства, то есть

Учитывая, что на ОДЗ указанный переход можно выполнить и в обратном направлении (большему положительному значению аргумента соответ% ствует большее значение функции), получаем, что на ОДЗ неравенство (1) равносильно неравенству (2). Коротко это можно записать так:

II.При 0 < a < 1 логарифмическая функция y = loga t убывает на всей своей области определения (то есть при t > 0), и поэтому большему значению функции соответствует меньшее значение аргумента. Следовательно, пе% реходя в неравенстве (1) от значений функции к значениям аргумента, мы должны знак неравенства изменить на противоположный, то есть

Учитывая, что на ОДЗ указанный переход можно выполнить и в обратном направлении (меньшему положительному значению аргумента соответству% ет большее значение функции), получаем, что при 0 < a < 1 неравенство (1) на его ОДЗ равносильно неравенству (5). Коротко это можно записать так:

388

§ 33. Решение логарифмических уравнений и неравенств

Суммируя полученные результаты, отметим, что

для решения неравенства вида loga f (x) > loga g (x) с помощью равно сильных преобразований необходимо учесть его ОДЗ, а при переходе от значений функции к значениям аргумента (то есть к выражени ям, стоящим под знаком логарифма) — значение a:

при a > 1 знак неравенства не меняется,

при 0 < a < 1 знак неравенства меняется на противоположный. )

Примеры использования этих ориентиров приведены в таблице 56.

З а м е ч а н и е. Системы неравенств, полученные для случаев І и ІІ, можно несколько упростить. Например, если в системе выполняются неравенство (2): f (x) > g (x) и неравенство (4): g (x) > 0, то из этих неравенств следует, что f (x) > 0. Следовательно, неравенство (3) этой системы выполняется автома% тически, когда выполняются неравенства (2) и (4), и его можно не записы% вать в эту систему (см. пункт 2 табл. 56).

Аналогично обосновывается, что в случае ІІ в системе неравенство (4) являет% ся следствием неравенств (3) и (5), и его также можно не записывать в систему.

Например, решим неравенство log5 (x2 – 2x) > log5 3.

log5 (x2 – 2x) > log5 3 x2 – 2x > 3.

(ОДЗ данного неравенства x2 – 2x > 0 учтено автоматически, поскольку, если x2 – 2x > 3, то выполняется и неравенство x2 – 2x > 0.)

Решаем неравенство x2 – 2x > 3. Тогда x2 – 2x – 3 > 0, отсюда (см. рисунок) x < –1 или x > 3 — решение заданного неравенства (его можно записать и так: (–×; –1) (3; +×)).

2. Решение более сложных логарифмических неравенств выполняется или с помощью равносильных преобразований данного неравенства (и при% ведения его к известному виду неравенств), или с помощью метода интер% валов.

Схема равносильных преобразований логарифмических неравенств пол% ностью аналогична схеме равносильных преобразований логарифмических уравнений:

1)учитываем ОДЗ данного неравенства;

2)следим за тем, чтобы на ОДЗ каждое преобразование можно было выполнить как в прямом, так и в обратном направлениях с сохранением верного неравенства.

Вэтом случае на ОДЗ каждое решение данного неравенства будет и реше% нием второго и, наоборот, каждое решение второго неравенства будет реше% нием первого, то есть эти неравенства будут равносильными (на ОДЗ).

Примеры решения логарифмических неравенств с помощью равносильных преобразований и методом интервалов и оформления такого решения приве%

дены в таблице 56. Рассмотрим еще несколько примеров.

389

РАЗДЕЛ 4. Показательная и логарифмическая функции

Примеры решения задач

Решим данное неравенство с помощью равносильных преобразований. Как и для уравнений, для этого достаточно учесть ОДЗ данного неравенства и следить за тем, чтобы на ОДЗ каждое преобразование можно было выпол" нить как в прямом, так и в обратном направлениях с сохранением верного неравенства. Поскольку на ОДЗ выражения, стоящие под знаком логариф% мов, положительны, то формулу loga b + loga c = loga (bc) для положитель% ных b и c можно применить как в прямом, так и в обратном направлениях. Таким образом, выполняя преобразование неравенства по этой формуле, по% лучим неравенство, равносильное данному (на его ОДЗ).

Чтобы применить свойства логарифмической функции, запишем число (–1) как значение логарифмической функции: –1 = log0,2 (0,2)–1 (понятно,

что эту формулу можно применить как в прямом, так и в обратном направле%

= (102 )−1 = (51 )−1 = 5.

Р е ш е н и е

x − 1 > 0,

ОДЗ: x + 3 > 0. Тогда x > 1.

На этой ОДЗ данное неравенство равносильно неравенству

390

§ 33. Решение логарифмических уравнений и неравенств

391