
Algebra_10kl_RU
.pdf



§26. Применение свойств функций к решению иррациональных уравнений
26.2.ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ДРУГИХ СПОСОБОВ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
Если при решении иррациональных уравнений мы используем уравнения следствия (как в § 24), то в конце приходится выполнять проверку получен ных корней. Но в тех случаях, когда эти решения — не рациональные числа, проверка с помощью подстановки полученных значений в исходное уравнение является достаточно сложной и требующей громоздких вычислений. Для та ких уравнений приходится применять равносильные преобразования на каж дом шагу решения. При этом необходимо помнить, что все равносильные пре образования уравнений или неравенств выполняются на ОДЗ данного уравне ния или неравенства (§ 17), поэтому, выполняя равносильные преобразова ния иррациональных уравнений, приходится учитывать ОДЗ данного урав нения. Достаточно часто в этих случаях используются также следующие рас суждения: для всех корней данного уравнения знаки левой и правой частей уравнения совпадают, поскольку при подстановке в данное уравнение числа, которое является его корнем, получаем верное числовое равенство. Исполь зуя последнее рассуждение, часто удается получить какое нибудь дополни тельное условие для корней данного уравнения и выполнить равносильные преобразования не на всей ОДЗ данного уравнения, а на некоторой его части.
Задача 1 |
|
|
Решите уравнение 2x + 1 − x + 1 = 1. |
|||||||||
|
|
|
Р е ш е н и е |
|
|
|
К о м м е н т а р и й |
|||||
|
|
|
|
|
|
|||||||
|
|
2x + 1l0, |
|
|
|
|
Выполним равносильные преобра |
|||||
|
|
|
|
|
|
зования данного уравнения. |
||||||
ОДЗ: x + 1l 0. |
|
|
|
|
|
|||||||
|
|
|
|
|
Учитывая, что все равносильные |
|||||||
Решение этой системы: x l − |
1 |
. |
преобразования выполняются на |
|||||||||
ОДЗ данного уравнения, зафиксиру |
||||||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|||
На ОДЗ данное уравнение равно |
ем его ОДЗ. |
|||||||||||
сильно уравнениям: |
|
|
|
|
|
При переносе члена (− x + 1) из |
||||||
|
2x + 1 = 1 + |
x + 1, |
|
|
|
левой части уравнения в правую с про |
||||||
( 2x + 1)2 = (1+ x + 1)2 |
, |
|
|
тивоположным знаком получаем |
||||||||
|
|
уравнение, равносильное данному. |
||||||||||
2x + 1 = 1+ 2 x + 1 + x + 1, |
В уравнении 2x + 1 = 1 + x + 1 |
|||||||||||
|
|
x − 1 = 2 |
x + 1. |
(1) |
обе части неотрицательные, следова |
|||||||
|
|
тельно, при возведении обеих частей |
||||||||||
Для всех корней уравнения (1) |
||||||||||||
в квадрат получим уравнение, равно |
||||||||||||
|
|
|
х – 1 l 0. |
|
(2) |
сильное данному, которое, в свою оче |
||||||
При этом условии уравнение (1) |
редь, равносильно уравнению (1). |
|||||||||||
равносильно уравнениям: |
|
|
|
Для всех корней уравнения (1) оно |
||||||||
( |
x − 1 |
)2 |
= |
( |
x + 1 |
)2 |
|
|
|
является верным числовым равен |
||
|
|
2 |
, |
|
|
|
ством. В этом равенстве правая часть |
|||||
х2 – 2х + 1 = 4(х + 1), |
|
|
|
|||||||||
|
|
|
2 x + 1 l 0 — неотрицательное число, |
|||||||||
|
х2 – 6х – 3 = 0. |
|
|
|
||||||||
|
|
|
|
тогда и левая часть является неотри |
||||||||
|
|
|
|
|
|
|
|
305 |
||||




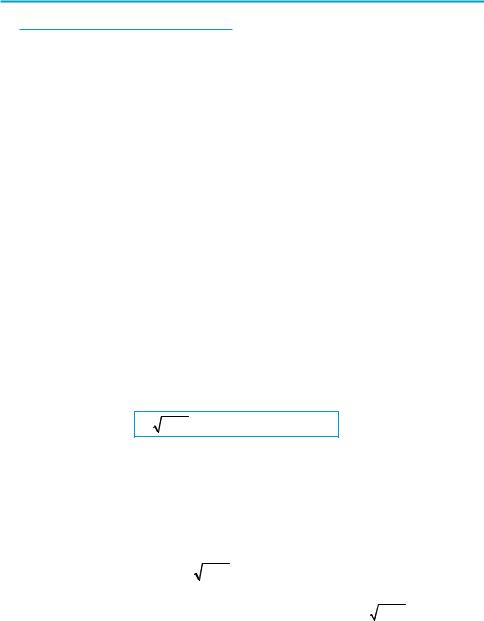



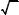 (1) достаточно с помощью равносильных преобразований записать его в виде:
(1) достаточно с помощью равносильных преобразований записать его в виде: