electrodynamics / Electromagnetic Field Theory - Bo Thide

A particularly simple rank-two tensor in 3 is the 3D Kronecker delta symbol i j, with the following properties:

Another common and useful tensor is the fully antisymmetric tensor of rank 3, also known as the Levi-Civita tensor

to be a tensor of rank n = 0 and a vector a tensor of rank n = 1. Consequently, the notation where a vector (tensor) is represented in its component form is called the tensor notation. A tensor of rank n =2 may be represented by a twodimensional array or matrix whereas higher rank tensors are best represented in their component forms (tensor notation).

In 4D, we have three forms of four-tensor fields of rank n. We speak of

• a contravariant four-tensor field, denoted A 1 2:::n (x ),

• a covariant four-tensor field, denoted A 1 2:::n (x ),

• a mixed four-tensor field, denoted A 1 2:::k (x ).

k+1:::n

The 4D metric tensor (fundamental tensor) mentioned above is a particularly important four-tensor of rank 2. In covariant component form we shall denote it g . This metric tensor determines the relation between an arbitrary contravariant four-vector a and its covariant counterpart a according to the following rule:

x3

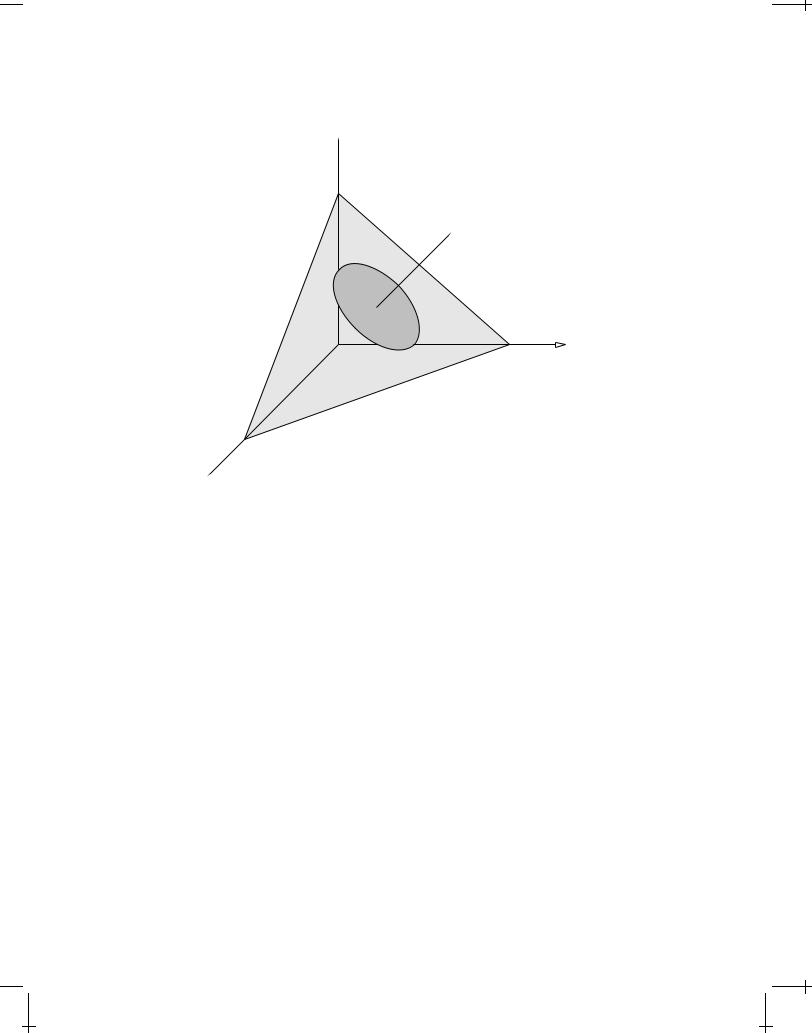
nˆ

d2x

x2

V

x1

FIGURE M.2: Terahedron-like volume element V containing matter.

where Fext is the external force and a is the acceleration of the volume element. In other words

Since both a and Fext=m remain finite whereas m=d2x ! 0 as V ! 0, one finds that in this limit

i=1

From the above derivation it is clear that Equation (M.28) above is valid not only in equilibrium but also when the matter in V is in motion.

for the jth component of the vector Txˆi , we can write Equation (M.28) on the preced-

ing page in component form as follows

i=1

Using Equation (M.30) above, we find that the component of the vector Tnˆ in the direction of an arbitrary unit vector mˆ is

We shall now show how one can use the momentum law (force equation) to derive the equation of motion for an arbitrary element of mass in the body. To this end we consider a part V of the body. If the external force density (force per unit volume) is denoted by f and the velocity for a mass element dm is denoted by v, we obtain

where, in the last step, Equation (M.30) was used. Setting dm = d3x and using the divergence theorem on the last term, we can rewrite the result as

Note that @v j=@t is the rate of change with time of the velocity component v j at a fixed point x = (x1;x1;x3).

END OF EXAMPLE M.1

unit vector is

(M.43)

On the other hand, the definition of the scalar product in terms of the inner product of complex vector with its own complex conjugate yields

END OF EXAMPLE M.3

In general relativity the metric tensor is not given a priori but is determined by the

Einstein equations.

END OF EXAMPLE M.4

Dyadic product

The dyadic product field A(x) a(x)b(x) with two juxtaposed vector fields a(x) and b(x) is the outer product of a and b. Operating on this dyad from the right and from the left with an inner product of an vector c one obtains

i.e., new vectors, proportional to a and b, respectively. In mathematics, a dyadic product is often called tensor product and is frequently denoted a b.

In matrix notation the outer product of a and b is written

which we identify with expression (M.15) on page 162, viz. a tensor in matrix notation.

Vector product

The vector product or cross product of two arbitrary 3D vectors a and b in ordinary 3 space is the vector

Here i jk is the Levi-Civita tensor defined in Equation (M.18) on page 163. Sometimes the vector product of a and b is denoted a ^b or, particularly in the Russian literature, [ab].

A spatial reversal of the coordinate system (x10;x20;x30) = ( x1; x2; x3) changes sign of the components of the vectors a and b so that in the new coordinate system a0 = a and b0 = b, which is to say that the direction of an ordinary vector is not dependent on the choice of directions of the coordinate axes. On the other hand, as is seen from Equation (M.54) above, the cross product vector c does not change sign. Therefore a (or b) is an example of a “true” vector, or polar vector, whereas c is an example of an axial vector, or pseudovector.

A prototype for a pseudovector is the angular momentum vector and hence the attribute “axial.” Pseudovectors transform as ordinary vectors under translations and proper rotations, but reverse their sign relative to ordinary vectors for any coordinate change involving reflection. Tensors (of any rank) which transform analogously to pseudovectors are called pseudotensors. Scalars are tensors of rank zero, and zero-rank pseudotensors are therefore also called pseudoscalars, an example being the pseudoscalar xˆi (xˆ j xˆk). This triple product is a representation of the i jk component of the Levi-Civita tensor i jk which is a rank three pseudotensor.

M.1.4 Vector analysis

The del operator

In 3 the del operator is a differential vector operator, denoted in Gibbs' notation by r and defined as

where xˆi is the ith unit vector in a Cartesian coordinate system. Since the operator in itself has vectorial properties, we denote it with a boldface nabla. In “component” notation we can write

In 4D, the contravariant component representation of the four-del operator is defined by

END OF EXAMPLE M.5

With the help of the del operator we can define the gradient, divergence and curl of a tensor (in the generalised sense).

From this we see that the boldface notation for the nabla and del operators is very handy as it elucidates the 3D vectorial property of the gradient.

In 4D, the four-gradient is a covariant vector, formed as a derivative of a four-scalar field (x ), with the following component form:

END OF EXAMPLE M.6