
electrodynamics / Electromagnetic Field Theory - Bo Thide
.pdf
8.5 RADIATION FROM A LOCALISED CHARGE IN ARBITRARY MOTION |
113 |
|
or
(t0 |
;x0)d3x0 = |
|
|
dq0 |
(8.60) |
|||
1 |
(x x0) v |
|||||||
ret |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cjx x0j |
|
|||
which leads to the expression
(t0 |
;x0) |
|
|
dq0 |
|
|
ret |
|
d3x0 |
= |
|
|
(8.61) |
|
|
jx x0j (x xc0) v |
||||
jx x0j |
|
|
||||
This is the expression to be used in the formulae (8.57) on page 111 for the retarded potentials. The result is (recall that j = v)
(t;x) = |
1 |
|
|
dq0 |
(8.62a) |
||||||
4"0 jx x0j |
(x xc0) v |
|
|||||||||
|
|
|
|||||||||
A(t;x) = |
0 |
|
|
|
vdq0 |
|
(8.62b) |
||||
4 jx x0j |
(x xc0) v |
|
|
|
|||||||
|
|
|
|||||||||
For a sufficiently small and well localised charge distribution we can, assuming that the integrands do not change sign in the integration volume, use the mean value theorem and the fact that V dq0 = q0 to evaluate these expressions to become
(t;x) = |
q0 |
1 |
|
|
= |
q0 1 |
(8.63a) |
|||
|
|
|
(x xc0) v |
|
|
|
|
|||
4"0 jx x0j |
|
4"0 s |
|
|||||||
A(t;x) = |
|
|
q0 |
|
|
|
|
v |
= |
q0 |
|
v |
= |
v |
(t;x) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(x xc0) v |
|
|
|
|
||||||||
where |
|
|
4"0c2 jx x0j |
|
4"0c2 s c2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s = x |
|
x0 |
|
|
|
(x x0) v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
x x0 |
|
|
v |
|
|
|
|
|
|
|
||||||
= x x0 |
|
|
1 |
|
jx x0j |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
c |
|
|
|
|
|
|
|
|||||||||||||||
= (x |
|
x0) |
|
|
x x0 |
|
v |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
jx x0j c |
|
|
|
|
|
|
|
|||||||||||
(8.63b)
(8.64a)
(8.64b)
(8.64c)
is the retarded relative distance. The potentials (8.63) are precisely the LiénardWiechert potentials which we derived in Section 5.3.2 on page 63 by using a covariant formalism.
It is important to realise that in the complicated derivation presented here, the observer is in a coordinate system which has an “absolute” meaning and the
Draft version released 13th November 2000 at 22:01. |
Downloaded from http://www.plasma.uu.se/CED/Book |
|
|

114 |
ELECTROMAGNETIC RADIATION |
|
|
|
? |
|
q0 |
jx x0jv |
x0(t) |
v(t0) |
|
c |
|
|
x0(t0) |
0 |
|
0 |
|
|
|
x x0
x x0
 x(t)
x(t)
FIGURE 8.3: Signals which are observed at the field point x at time t were generated at the source point x0(t0). After time t0 the particle, which moves with nonuniform velocity, has followed a yet unknown trajectory. Extrapolating tangentially the trajectory from x0(t0), based on the velocity v(t0), defines the virtual simultaneous coordinate x0(t).
velocity v is that of the particle, whereas in the covariant derivation two frames of equal standing were moving relative to each other with v. Expressed in the four-potential, Equation (5.45) on page 62, the Liénard-Wiechert potentials become
A (x ) = |
q0 |
1 |
; |
v |
= ( ;cA) |
(8.65) |
|
|
|
|
|
||||
4 "0 |
s |
|
|||||
|
|
cs |
|
||||
The Liénard-Wiechert potentials are applicable to all problems where a spatially localised charge emits electromagnetic radiation, and we shall now study such emission problems. The electric and magnetic fields are calculated from the potentials in the usual way:
B(t;x) = r A(t;x) |
@A(t;x) |
(8.66a) |
|
E(t;x) = r (t;x) |
(8.66b) |
||
|
|||
@t |
8.5.2 Radiation from an accelerated point charge
Consider a localised charge q0 and assume that its trajectory is known experimentally as a function of retarded time
x0 = x0(t0) |
(8.67) |
Downloaded from http://www.plasma.uu.se/CED/Book |
Draft version released 13th November 2000 at 22:01. |
|
|

8.5 RADIATION FROM A LOCALISED CHARGE IN ARBITRARY MOTION |
115 |
|
(in the interest of simplifying our notation, we drop the subscript “ret” on t0 from now on). This means that we know the trajectory of the charge q0, i.e., x0, for all times up to the time t0 at which a signal was emitted in order to precisely arrive at the field point x at time t. Because of the finite speed of propagation of the fields, the trajectory at times later than t0 is not (yet) known.
The retarded velocity and acceleration at time t0 are given by
v(t0) = |
dx0 |
|
|
|
|
(8.68a) |
|
dt0 |
|
d2x0 |
|||||
|
|
|
|||||
a(t0) = v˙(t0) = |
dv |
= |
(8.68b) |
||||
dt0 |
dt02 |
||||||
|
|
|
|
|
|||
As for the charge coordinate x0 itself, we have in general no knowledge of the velocity and acceleration at times later than t0, in particular not at the time of observation t. If we choose the field point x as fixed, application of (8.68) to the relative vector x x0 yields
|
|
d |
(x x0(t0)) = v(t0) |
(8.69a) |
|
|
dt0 |
||||
|
d2 |
(x x0(t0)) = v˙(t0) |
(8.69b) |
||
|
dt02 |
|
|||
The retarded time t0 can, at least in principle, be calculated from the implicit relation
t0 = t0(t;x) = t |
|
jx x0(t0)j |
(8.70) |
|
c |
|
and we shall see later how this relation can be taken into account in the calculations.
According to formulae (8.66) on the facing page the electric and magnetic fields are determined via differentiation of the retarded potentials at the observation time t and at the observation point x. In these formulae the unprimed r, i.e., the spatial derivative differentiation operator r = xˆi@=@xi means that we differentiate with respect to the coordinates x = (x1;x2;x3) while keeping t fixed, and the unprimed time derivative operator @=@t means that we differentiate with respect to t while keeping x fixed. But the Liénard-Wiechert potentialsand A, Equations (8.63) on page 113, are expressed in the charge velocity v(t0) given by Equation (8.68a) and the retarded relative distance s(t0;x) given by Equation (8.64) on page 113. This means that the expressions for the potentials and A contain terms which are expressed explicitly in t0, which in turn is expressed implicitly in t via Equation (8.70). Despite this complication it is
Draft version released 13th November 2000 at 22:01. |
Downloaded from http://www.plasma.uu.se/CED/Book |
|
|

116 |
ELECTROMAGNETIC RADIATION |
|
possible, as we shall see below, to determine the electric and magnetic fields and associated quantities at the time of observation t. To this end, we need to investigate carefully the action of differentiation on the potentials.
The differential operator method We introduce the convention that a differential operator embraced by parentheses with an index x or t means that the operator in question is applied at constant x and t, respectively. With this convention, we find that
@ |
|
|
x |
|
x0(t0) = |
|
x |
x0 |
|
|
@ |
|
|
x |
|
x0 |
(t0)#= |
|
(x x0) v |
(8.71) |
||||||
@t |
|
|
|
x |
|
|
|
|
|
|||||||||||||||||
0 |
|
|
j |
|
x |
|
@t |
0 |
|
|
|
|
|
x |
|
x |
0j |
|
||||||||
|
x |
|
|
|
0j |
|
|
x " |
|
|
|
|
j |
|
|
|
||||||||||
Furthermore, by applying the operator (@=@t)x to Equation (8.70) on the previous page we find that
@t0 |
|
|
@ |
|
|
|
x |
|
x0 |
(t0(t;x)) |
|
||||||
|
|
= 1 |
|
|
|
j |
|
|
|
|
j |
|
|
||||
@t |
@t |
|
|
c |
|
||||||||||||
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||
|
|
= 1 |
|
|
|
@ |
|
|
|
jx x0j |
|
@t0 |
|
(8.72) |
|||
|
|
@t |
|
|
|
@t |
|||||||||||
|
|
|
|
|
0 |
|
|
c |
|
|
|||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
(x x0) v @t0
= 1 + c jx x0j @t x
This is an algebraic equation in (@t0=@t)x which we can solve to obtain
@t0 |
|
= |
jx x0j |
= |
jx x0j |
(8.73) |
|
@t x |
|||||||
|
jx x0j(x x0) v=c |
|
s |
|
|||
where s = s(t0;x) is the retarded relative distance given by Equation (8.64) on page 113. Making use of Equation (8.73) above, we obtain the following useful operator identity
@ |
|
= |
@t0 |
|
@ |
|
= |
jx x0j |
|
@ |
|
(8.74) |
|
@t x |
@t x @t0 x |
@t0 x |
|||||||||||
|
|
s |
|
||||||||||
Likewise, by applying (r)t to Equation (8.70) on the preceding page we obtain
(r) |
t0 |
= |
|
(r) |
|
jx x0(t0(t;x))j |
= |
x x0 |
(r) |
(x |
|
x0) |
|||
|
c jx x0j |
|
|||||||||||||
t |
|
|
|
t |
c |
t |
|
(8.75) |
|||||||
|
|
= |
|
x x0 |
+ |
(x x0) v |
(r) |
t0 |
|
|
|
|
|||
|
|
|
c jx x0j |
|
c jx x0j |
t |
|
|
|
|
|
||||
Downloaded from http://www.plasma.uu.se/CED/Book |
Draft version released 13th November 2000 at 22:01. |
|
|
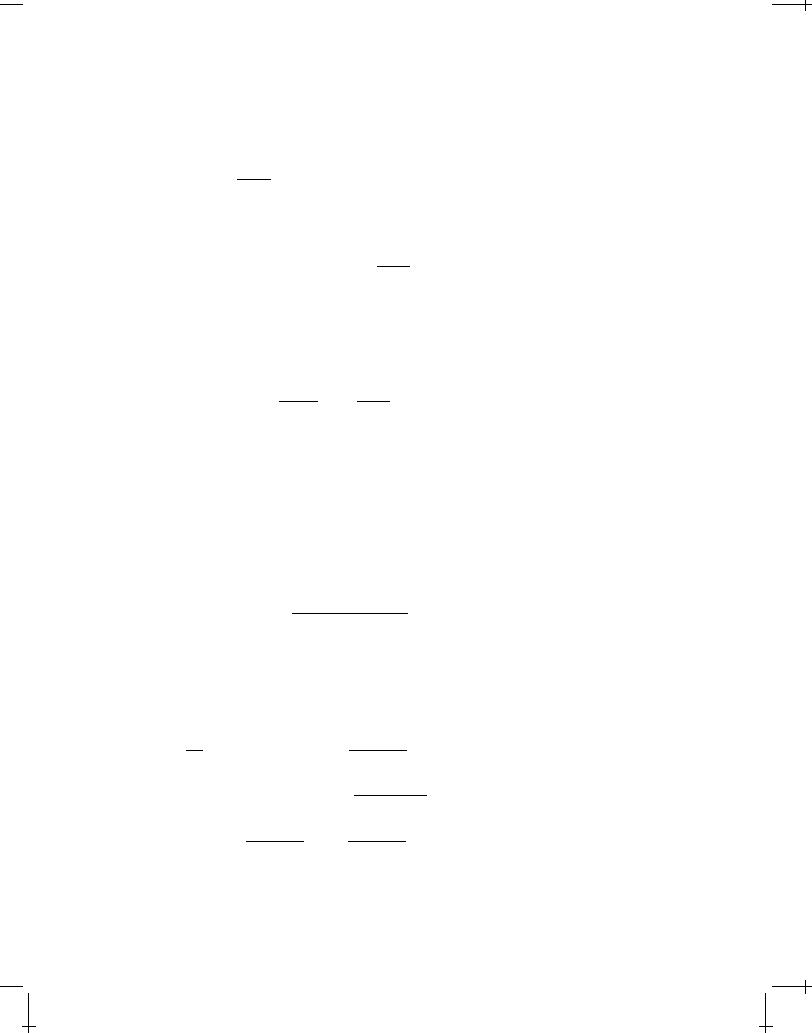
8.5 RADIATION FROM A LOCALISED CHARGE IN ARBITRARY MOTION |
117 |
|
This is an algebraic equation in (r)t with the solution |
|
||||
(r) |
t0 |
= |
|
x x0 |
(8.76) |
t |
|
|
cs |
|
|
which gives the following operator relation when (r)t is acting on an arbitrary function of t0 and x:
(r) |
= (r) |
t0 |
@ |
|
+(r) |
|
= |
|
x x0 |
|
@ |
+(r) |
|
(8.77) |
@t0 x |
|
|
|
|
||||||||||
t |
t |
|
|
t0 |
|
cs |
@t0 x |
t0 |
|
|||||
With the help of the rules (8.77) and (8.74) we are now able to replace t by t0 in the operations which we need to perform. We find, for instance, that
r (r )t = r |
|
1 |
|
|
|
|
q0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
4 "0 |
|
s |
|
|
|
|
|
|
|
|
(8.78a) |
|||||||||||||||||||||||||
|
|
|
|
|
q0 |
|
|
|
|
|
x x0 |
|
|
|
|
v |
|
|
|
x x0 |
|
@s |
|
|||||||||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
j |
|
x |
0j |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
4 " |
s2 x |
|
|
|
|
c cs @t |
|
|||||||||||||||||||||||||||
@A |
|
|
|
@A |
|
|
|
|
@ |
|
|
|
0 q0v |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
x |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
@t |
@t |
|
@t 4 s |
|
|
|
|
|
|
(8.78b) |
||||||||||||||||||||||||||
|
|
|
|
|
q0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
@s |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
= |
|
|
|
|
|
|
|
|
|
|
|
x |
|
x0 |
|
sv˙ |
|
x |
|
x0 |
v |
|
|
|
|||||||||||
|
|
4 " |
|
|
|
|
|
|
|
|
|
@t |
|
|||||||||||||||||||||||
|
|
|
c2 s3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
x |
|
Utilising these relations in the calculation of the E field from the LiénardWiechert potentials, Equations (8.63) on page 113, we obtain
E(t;x) = r |
@A |
|
|
|
|
|
|
|
|
|
|||
@t |
|
|
|
|
|
|
|
|
|||||
= |
q0 |
|
|
|
(x x0) jx x0jv=c |
|
|
|
|
|
(8.79) |
||
|
|
|
|
|
|
|
|
||||||
4 "0 s2 |
jx x0j |
|
|
|
|
|
|||||||
|
|
|
|
|
|
(x x0) jx x0jv=c @s |
|
jx x0jv˙ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
cs |
|
@t0 x |
c2 |
|||||
Starting from expression (8.64a) on page 113 for the retarded relative distance s(t0;x), we see that we can evaluate (@s=@t0)x in the following way
@s
@t0
|
= |
@ |
|
|
|
|
x |
|
x0 |
(x x0) v |
|
|
|
|
|
|
|
|
|
|
||||||||
|
@t |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
= |
|
@ |
|
|
x |
|
x0 |
(t0) |
1 |
|
|
|
@"x x0(t0)# v |
|
(x |
|
x0) |
|
@v(t0) |
|
(8.80) |
||||||
|
|
|
|
|
|
|
|
|
@t0 1 |
|||||||||||||||||||
|
|
|
@t0 |
|
|
|
c 0 @t0 |
|
|
|
|
|
||||||||||||||||
|
= |
|
(x x0) v |
+ |
v2 |
|
|
(x x0) v˙ |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
jx x0j |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|||||||||
Draft version released 13th November 2000 at 22:01. |
Downloaded from http://www.plasma.uu.se/CED/Book |
|
|

118 |
ELECTROMAGNETIC RADIATION |
|
where Equation (8.71) on page 116 and Equations (8.68) on page 115, respectively, were used. Hence, the electric field generated by an arbitrarily moving charged particle at x0(t0) is given by the expression
E(t;x) = |
q0 |
|
(x |
|
|
x0) |
|
jx x0jv |
|
|
|
1 |
|
v2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
c2 . |
|
|
||||||||||||||||||||
4 "0 s3 * |
|
|
|
+c -, |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
x |
Coulomb field when v ! 0 |
|
v |
|
(8.81) |
|||||||||||||||||||
|
|
|
|
|
x0 |
|
(x |
|
|
x+/,0) |
j |
x |
|
x0 |
j |
v˙ |
|
|||||||||||
|
|
+ |
* |
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
c |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Radiation field |
|
|
|
|
|
|
|
|
||||||||||
The first part of the field, the velocity field, tends to the ordinary Coulomb field when v ! 0 and does not contribute to the radiation. The second part of the field, the acceleration field, is radiated into the far zone and is therefore also called the radiation field.
From Figure 8.5.2 on page 114 we see that the position the charged particle would have had if at t0 all external forces would have been switched off so that the trajectory from then on would have been a straight line in the direction of the tangent at x0(t0) is x0(t), the virtual simultaneous coordinate. During the arbitrary motion, we interpret x x0 as the coordinate of the field point x relative to the virtual simultaneous coordinate x0(t). Since the time it takes from a signal to propagate (in the assumed vacuum) from x0(t0) to x is jx x0j=c, this relative vector is given by
x x0 = (x x0) jx x0jv c
This allows us to rewrite Equation (8.81) in the following way
E(t;x) = |
q0 |
(x |
x |
) 1 |
|
v2 |
|
+(x |
|
x0) |
|
(x x0) v˙ |
|
c2 |
|
|
|||||||||
|
4 "0 s3 |
0 |
|
|
|
c2 |
||||||
In a similar manner we can compute the magnetic field:
B(t;x) = r |
|
A |
|
(r) |
t |
A = (r) |
t0 |
A |
x x0 |
|
|
@ |
A |
||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
cs |
|
|
|
@t0 x |
||||||
= |
|
|
q0 |
|
x x0 |
v |
|
x x0 |
|
@A |
|
|
|||||||
|
|
|
|
|
@t x |
|
|||||||||||||
|
4 "0c2 s2 jx x0j |
|
c jx x0j |
|
|
||||||||||||||
(8.82)
(8.83)
(8.84)
where we made use of Equation (8.63) on page 113 and formula (8.74) on page 116. But, according to (8.78a),
x x0 |
(r) |
= |
q0 |
x x0 |
v |
(8.85) |
|
||||||
c jx x0j |
t |
|
4 "0c2 s2 jx x0j |
|
|
|
Downloaded from http://www.plasma.uu.se/CED/Book |
Draft version released 13th November 2000 at 22:01. |
|
|

8.5 RADIATION FROM A LOCALISED CHARGE IN ARBITRARY MOTION |
119 |
|
so that
x x0
B(t;x) = c jx x0j (r )t
xx0
=c jx x0j E(t;x)
@A |
|
@t x |
(8.86) |
The radiation part of the electric field is obtained from the acceleration field in formula (8.81) on the preceding page as
Erad(t;x) = |
|
lim E(t;x) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
jx x0j!1 |
|
|
|
|
|
|
|
|
jx x0jv |
|
|
|
|
||
= |
|
q0 |
(x |
|
x0) |
|
(x |
|
x0) |
|
|
|
v˙ |
(8.87) |
||
4 "0c2 s3 |
||||||||||||||||
|
|
|
|
|
c |
|
||||||||||
= |
|
q0 |
(x x0) [(x x0) v˙] |
|
|
|
|
|
||||||||
|
4 "0c2 s3 |
|
|
|
|
|
||||||||||
where in the last step we again used formula (8.82) on the facing page. Using this formula and formula (8.86) above, the radiation part of the magnetic field can be written
Brad(t;x) = |
x x0 |
Erad(t;x) |
(8.88) |
c jx x0j |
|
|
|
The direct method An alternative to the differential operator transformation technique just described is to try to express all quantities in the potentials directly in t and x. An example of such a quantity is the retarded relative distance s(t0;x). According to Equation (8.64) on page 113, the square of this retarded relative can be written
|
2 |
|
(x x0) v |
|
(x x0) v |
|
2 |
|||
s2(t0;x) = x x0 |
|
2 x x0 |
|
|
|
+ |
|
|
|
(8.89) |
|
|
|
||||||||
|
|
c |
|
c |
|
|
||||
If we use the following handy identity
|
(x x0) v |
2 + |
(x x0) v |
2 |
|
|
|
||||||
|
|
c |
|
|
|
c |
|
|
|
|
|||
|
= |
jx x0j2 v2 |
cos2 |
0 |
+ |
jx x0j2 v2 |
sin2 |
0 |
(8.90) |
||||
|
|
c2 |
|
|
|
|
|
c2 |
|
|
|||
|
= |
jx x0j2 v2 |
(cos2 0 +sin2 0) = |
jx x0j2 v2 |
|
||||||||
|
|
c2 |
|
|
|
|
|
|
|
c2 |
|
||
Draft version released 13th November 2000 at 22:01. |
Downloaded from http://www.plasma.uu.se/CED/Book |
|
|

120 |
ELECTROMAGNETIC RADIATION |
|
we find that |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
x0) |
|
v 2 |
|
|
x |
x0 |
2 v2 |
|
(x |
x0) |
|
v |
2 |
|
c |
|
|
= |
j |
|
c2j |
|
|
|
c |
|
|
(8.91) |
Furthermore, from Equation (8.82) on page 118, we obtain the following identity:
(x x0) v = (x x0) v |
|
|
|
|
|
|
(8.92) |
|||||||
which, when inserted into Equation (8.91), yields the relation |
||||||||||||||
(x |
x0) |
|
v 2 |
|
|
x |
x0 |
2 v2 |
|
(x |
x0) |
|
v |
2 |
|
|
|
|
= |
j |
|
c2j |
|
|
|
|
|
|
(8.93) |
|
c |
|
|
|
|
|
c |
|
|
|||||
Inserting the above into expression (8.89) on the previous page for s2, this expression becomes
s2 = x x0 |
|
2 |
|
2 x x0 |
(x |
|
x0) |
|
v |
+ j |
x |
x0 |
2 |
v |
2 |
|
(x |
x0) |
|
v |
2 |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
= (x |
|
|
x0) |
|
|
jx x0jv |
|
2 |
|
|
(x x0) v |
2 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
(8.94) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x x0(t)) v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= (x |
|
x |
|
(t))2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
j |
x |
|
x |
0j |
2 |
|
|
(x x0) v |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
where in the penultimate step we used Equation (8.82) on page 118.
What we have just demonstrated is that, in the case the particle velocity at time t can be calculated or projected, the retarded distance s in the LiénardWiechert potentials (8.63) can be expressed in terms of the virtual simultaneous coordinate x0(t), viz., the point at which the particle will have arrived at time t, i.e., when we obtain the first knowledge of its existence at the source point x0 at the retarded time t0, and in the field coordinate x(t), where we make our observations. We have, in other words, shown that all quantities in the definition of s, and hence s itself, can, when the motion of the charge is somehow known, be expressed in terms of the time t alone. I.e., in this special case we are able to express the retarded relative distance as s = s(t;x) and we do not have to involve the retarded time t0 or transformed differential operators in our calculations.
Downloaded from http://www.plasma.uu.se/CED/Book |
Draft version released 13th November 2000 at 22:01. |
|
|

8.5 RADIATION FROM A LOCALISED CHARGE IN ARBITRARY MOTION |
121 |
|
Taking the square root of both sides of Equation (8.94) on the preceding page, we obtain the following alternative final expressions for the retarded relative distance s in terms of the charge's virtual simultaneous coordinate x0(t):
s(t;x) = |
j |
x |
|
x |
0j |
2 |
|
|
(x x0) v |
2 |
|
(8.95a) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
v2 |
|
|
|
|
|
||||||
= jx x0j 1 |
|
sin2 0 |
|
|
|
|
(8.95b) |
||||||||||||||
c2 |
|
|
|
|
|||||||||||||||||
= |
|
x |
|
x |
|
2 |
1 |
|
|
|
v2 |
|
|
(x x0) v |
2 |
(8.95c) |
|||||
j |
|
0j |
|
|
c2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
c |
|
|
|||||||||
Using Equation (8.95c) and standard vector analytic formulae, we obtain
rs2 = r :x |
|
x |
|
2 1 |
|
|
v2 |
|
|
|
(x x0) v |
2; |
|
||
|
0j |
c2 |
|
||||||||||||
j |
|
|
|
|
c |
|
|||||||||
= 2 (x x0) 1 |
v2 |
|
vv |
(x x0) |
(8.96) |
||||||||||
|
+ |
|
|
|
|||||||||||
c2 |
c2 |
|
|||||||||||||
v v
= 2 &(x x0) + c c (x x0))'
which we shall use in the following example of a uniformly, unaccelerated motion of the charge.
THE FIELDS FROM A UNIFORMLY MOVING CHARGE
In the special case of uniform motion, the localised charge moves in a field-free, isolated space and we know that it will not be affected by any external forces. It will therefore move uniformly in a straight line with the constant velocity v. This gives us the possibility to extrapolate its position at the observation time, x0(t), from its position at the retarded time, x0(t0). Since the particle is not accelerated, v˙ 0, the virtual simultaneous coordinate x0 will be identical to the actual simultaneous coordinate of the particle at time t, i.e., x0(t) = x0(t). As depicted in Figure 8.5.2 on page 114, the angle between x x0 and v is 0 while then angle between x x0 and v is 0.
We note that in the case of uniform velocity v, time and space derivatives are closely related in the following way when they operate on functions of x(t) :
@ |
!v r |
(8.97) |
@t |
Hence, the E and B fields can be obtained from formulae (8.66) on page 114, with the
EXAMPLE
8.1
Draft version released 13th November 2000 at 22:01. |
Downloaded from http://www.plasma.uu.se/CED/Book |
|
|

122 |
ELECTROMAGNETIC RADIATION |
|
potentials given by Equations (8.63) on page 113 as follows:
E = r |
|
@A |
|
|
|
|
|
|
1 @v |
|
|
|
|
|
|
|
|
|
v @ |
|
|||||||||||||||||||
|
|
|
|
|
|
|
= r |
|
|
|
|
|
= r |
|
|
|
|
|
|
||||||||||||||||||||
|
@t |
|
c2 |
@t |
c2 |
@t |
|
||||||||||||||||||||||||||||||||
= |
|
|
r |
|
+ |
v |
|
|
|
|
v |
|
r |
|
|
|
[= |
|
Z |
|
vv |
|
[r |
|
|
|
|
|
|
|
(8.98a) |
||||||||
|
|
|
|
|
|
|
c Zc |
|
|
|
|
1 c2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
vv |
|
1[ r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= Zc2 |
|
|
|
|
|
|
|
|
|
|
v |
|
|
v |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
B = r A = r Zc2 |
[=r |
|
|
= |
|
|
|
r |
|
||||||||||||||||||||||||||||||
c2 |
c2 |
|
|||||||||||||||||||||||||||||||||||||
|
|
v |
|
|
|
|
v |
|
|
|
|
|
|
v |
|
|
|
|
v |
|
vv |
1[ r |
(8.98b) |
||||||||||||||||
= |
|
|
\Z |
|
|
r [ |
|
r ]= |
|
Zc2 |
|||||||||||||||||||||||||||||
c2 |
c |
c |
c2 |
||||||||||||||||||||||||||||||||||||
= |
v |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Here 1 = xˆi xˆi is the unit dyad and we used the fact that v v 0. What remains is just to express r in quantities evaluated at t and x.
From Equation (8.63a) on page 113 and Equation (8.96) on the previous page we find that
r = |
|
q0 |
1 |
|
= |
q0 |
|
rs |
2 |
|||||
|
|
r |
|
|
|
|
|
|
||||||
4"0 |
s |
8"0 s3 |
(8.99) |
|||||||||||
|
|
|
q0 |
|
|
v |
|
v |
||||||
|
|
|
|
|
|
(x x0)[] |
||||||||
= |
|
\(x x0) + |
|
|
Zc |
|||||||||
4"0 s3 |
c |
|||||||||||||
When this expression for r is inserted into Equation (8.98a), the following result
|
|
vv |
|
|
|
|
|
q0 |
|
|
|
vv |
|
|
2 |
|
|
|
|||||||||
E(t;x) = Zc2 |
1[ r = |
|
|
|
|
|
|
|
|
|
|
|
1[ rs |
|
|
|
|
||||||||||
8"0 s3 |
Zc2 |
|
|
|
|
||||||||||||||||||||||
|
|
q0 |
|
|
v |
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
||||||||
= |
|
|
|
^(x x0) + |
|
|
Zc |
(x x0)[ |
|
|
|
|
|||||||||||||||
4"0 s3 |
c |
|
|
|
|
||||||||||||||||||||||
|
|
|
v v |
|
|
|
|
|
|
|
vv |
|
v |
v |
|
|
|
|
|||||||||
|
|
|
|
|
|
(x x0)[ |
|
|
|
|
\c |
Zc |
(x |
x0)[]`_ |
|
||||||||||||
|
|
c |
Zc |
c2 |
|
|
(8.100) |
||||||||||||||||||||
|
|
q0 |
|
|
v |
|
v |
|
|
|
|
|
|
|
|
|
v2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= |
|
a(x x0) + |
|
|
|
|
|
(x x0)[ (x x0) |
|
|
|
||||||||||||||||
4"0 s3 |
c |
Zc |
|
c2 |
|
||||||||||||||||||||||
v v (x x0)[cb c Zc
|
q0 |
v2 |
||
= |
|
(x x0) 1 |
|
|
4"0 s3 |
2 |
|||
follows. Of course, the same result also follows from Equation (8.83) on page 118 with v˙ 0 inserted.
From Equation (8.100) we conclude that E is directed along the vector from the simultaneous coordinate x0(t) to the field (observation) coordinate x(t). In a similar way, the magnetic field can be calculated and one finds that
|
0q0 |
|
v2 |
1 |
|
|
|
B(t;x) = |
|
1 |
|
v (x x0) = |
|
v E |
(8.101) |
4 s3 |
c2 |
c2 |
|||||
Downloaded from http://www.plasma.uu.se/CED/Book |
Draft version released 13th November 2000 at 22:01. |
|
|
