electrodynamics / Electromagnetic Field Theory - Bo Thide

The need for the absolute value of the expression for s is obvious in the case when v=c 1=n because then the second term can be larger than the first term; if v=c 1=n we recover the well-known vacuum case but with modified phase speed. We also note that the retarded and advanced times in the medium are [cf. Equation (3.34) on page 41]

so that the usual time interval t t0 between the time measured at the point of observation and the retarded time in a medium becomes

For v=c 1=n, the retarded distance s, and therefore the denominators in Equations (8.200) vanish when

In the direction defined by this angle c, the potentials become singular. During the time interval t t0 given by expression (8.203) above, the field exists within a sphere of radius jx x0jaround the particle while the particle moves a distance

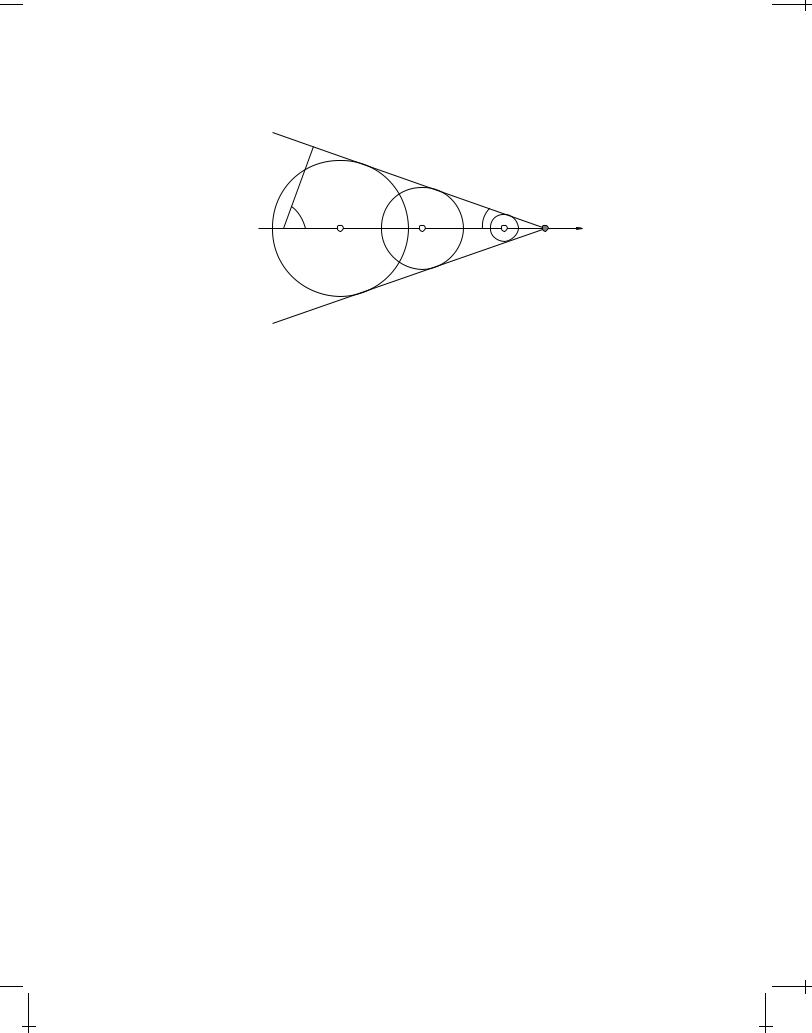
FIGURE 8.9: Instantaneous picture of the expanding field spheres from a point charge moving with constant speed v=c > 1=n in a medium where

ˇ

n > 1. This generates a Vavilov-Cerenkov shock wave in the form of a cone.

along the direction of v.

In the direction c where the potentials are singular, all field spheres are tangent to a straight cone with its apex at the instantaneous position of the particle and with the apex half angle c defined according to

This cone of potential singularities and field sphere circumferences propagates

a post-graduate student in S. I. Vavilov's research group at the Lebedev Institute in Moscow.

ˇ

Vavilov wrote a manuscript with the experimental findings, put Cerenkov as the author, and submitted it to Nature. In the manuscript, Vavilov explained the results in terms of radioactive particles creating Compton electrons which gave rise to the radiation (which was the correct interpretation), but the paper was rejected. The paper was then sent to Physical Review and was, after some controversy with the American editors who claimed the results to be wrong, eventually published in 1937. In the same year, I .E. Tamm and I. M. Frank published the theory for the effect (“the singing electron”). In fact, predictions of a similar effect had been made as early as 1888 by Heaviside, and by Sommerfeld in his 1904 paper “Radiating body moving with velocity of light”. On May 8, 1937, Sommerfeld sent a letter to Tamm via Austria, saying that he was surprised that his old 1904 ideas were now becoming interesting. Tamm,

ˇ

Frank and Cerenkov received the Nobel Prize in 1958 “for the discovery and the interpretation

ˇ

of the Cerenkov effect” [V. L. Ginzburg, private communication].

In order to make some quantitative estimates of this radiation, we note that we can describe the motion of each charged particle q0 as a current density:

This Fourier component can be used in the formulae derived for a linear current in Subsection 8.3.1 if only we make the replacements

In this manner, using j! from Equation (8.209), the resulting Fourier trans-

ˇ

forms of the Vavilov-Cerenkov magnetic and electric radiation fields can be calculated from the expressions (8.3a) and (8.3b) on page 98, respectively.

The total energy content is then obtained from Equation (8.12) on page 101 (integrated over a closed sphere at large distances). For a Fourier component one obtains [cf. Equation (8.15) on page 101]

where is the angle between the direction of motion, xˆ01, and the direction to

ˆ

the observer, k. The integral in (8.211) is singular of a “Dirac delta type.” If we limit the spatial extent of the motion of the particle to the closed interval [ X;X] on the x0 axis we can evaluate the integral to obtain

which has a maximum in the direction c as expected. The magnitude of this maximum grows and its width narrows as X !1. The integration of (8.212) over therefore picks up the main contributions from c. Consequently,

we can set sin2 sin2 c and the result of the integration is

The integral (8.213) is strongly in peaked near = c=(nv), or, equivalently, near cos c =c=(nv) so we can extend the integration limits to 1without introducing too much error. Via yet another variable substitution we can therefore approximate

leading to the final approximate result for the total energy loss in the frequency interval (!;!+d!)

As mentioned earlier, the refractive index is usually frequency dependent. Realising this, we find that the radiation energy per frequency unit and per unit length is

This result was derived under the assumption that v=c > 1=n(!), i.e., under the condition that the expression inside the parentheses in the right hand side is positive. For all media it is true that n(!) ! 1 when ! !1, so there exist al-

ˇ

ways a highest frequency for which we can obtain Vavilov-Cerenkov radiation from a fast charge in a medium. Our derivation above for a fixed value of n is valid for each individual Fourier component.

Bibliography

[1]R. BECKER, Electromagnetic Fields and Interactions, Dover Publications, Inc., New York, NY, 1982, ISBN 0-486-64290-9.

[2]V. L. GINZBURG, Applications of Electrodynamics in Theoretical Physics and Astrophysics, Revised third ed., Gordon and Breach Science Publishers, New York, London, Paris, Montreux, Tokyo and Melbourne, 1989, ISBN 2- 88124-719-9.

[3]J. D. JACKSON, Classical Electrodynamics, third ed., Wiley & Sons, Inc., New York, NY . . . , 1999, ISBN 0-471-30932-X.

[4]J. B. MARION, AND M. A. HEALD, Classical Electromagnetic Radiation, second ed., Academic Press, Inc. (London) Ltd., Orlando, . . . , 1980, ISBN 0- 12-472257-1.

[5]W. K. H. PANOFSKY, AND M. PHILLIPS, Classical Electricity and Magnetism, second ed., Addison-Wesley Publishing Company, Inc., Reading, MA . . . , 1962, ISBN 0-201-05702-6.

[6]J. VANDERLINDE, Classical Electromagnetic Theory, John Wiley & Sons, Inc., New York, Chichester, Brisbane, Toronto, and Singapore, 1993, ISBN 0-471- 57269-1.

F

Formulae

F.1 The Electromagnetic Field

F.1.1 Maxwell's equations

F.2.2 The far fields from an extended source distribution

0 0