
матем.4контр
..pdf
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «Заочная физико-техническая школа
Московского физико-технического института (государственного университета)»
МАТЕМАТИКА
Тригонометрические функции и уравнения
Задание №4 для 10-х классов (2012 – 2013 учебный год)
г. Долгопрудный, 2012

2012-2013 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения
Составитель: Ф.О. Сергеев, преподаватель ФЗФТШ при МФТИ.
Математика: задание №4 для 10-х классов (2012 – 2013 учебный год), 2012, 28 с.
Дата отправления заданий по физике и математике – 28 января 2013 г.
Учащийся должен стараться выполнять все задачи и контрольные вопросы в заданиях. Некоторая часть теоретического материала, а также часть задач и контрольных вопросов, являются сложными и потребуют от учащегося больше усилий при изучении и решении. В целях повышения эффективности работы с материалом они обозначены символом «*» (звѐздочка). Мы рекомендуем приступать к этим задачам и контрольным вопросам в последнюю очередь, разобравшись вначале с более простыми.
Составитель:
Сергеев Фѐдор Олегович
Подписано в печать 26.12.12. Формат 60×90 1/16. Бумага типографская. Печать офсетная. Усл. печ. л. 1,75. Уч.-изд. л. 1,5. Тираж 650. Заказ №34-з.
Заочная физико-техническая школа Московского физико-технического института (государственного университета)
ООО «Печатный салон ШАНС»
Институтский пер., 9, г. Долгопрудный, Москов. обл., 141700, ЗФТШ, тел./факс (495) 408-51-45 – заочное отделение,
тел./факс (498) 744-63-51 – очно-заочное отделение, тел. (499) 755-55-80 – очное отделение.
e-mail: zftsh@mail.mipt.ru
Наш сайт: www.school.mipt.ru
© ЗФТШ, 2012
2012, ЗФТШ МФТИ, Сергеев Фѐдор Олегович
2
2012-2013 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения
1.Тригонометрические функции
1.1.Понятие тригонометрической функции
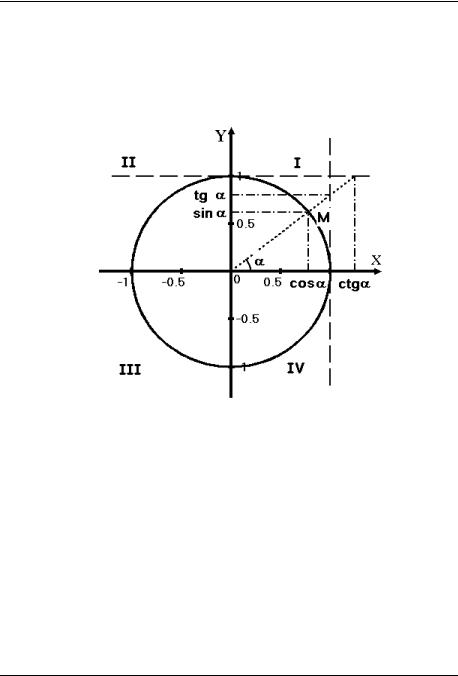
Рассмотрим окружность радиуса 1 с центром в начале координат (рис.1). Окружность разбивает плоскость на 4 части, называемые чет-
вертями (I, II, III, IV).
Рис. 1
Рассмотрим произвольный угол , отсчитываемый от положительного направления оси Х против часовой стрелки. Точка М, лежащая на пересечении стороны угла и окружности, имеет координаты x, y , где x cos , y sin . Таким образом, тригонометрические функции синуса и косинуса – это зависимости, соответственно, ординаты и абсциссы точки на тригонометрическом круге, соответствующей данному углу, от величины данного угла.
Тригонометрические функции тангенса и котангенса данного угла задаются как отношение, соответственно, синуса этого угла к его косинусу и наоборот, их геометрическая интерпретация показана на рис. 1.
2012, ЗФТШ МФТИ, Сергеев Фѐдор Олегович
3
2012-2013 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения
tg cossin ; ctg cossin .
Теперь очевидными становятся условия области определения и области значения этих функций.
|
|
|
|
|
|
cos |
sin |
tg |
ctg |
D f |
|
|
cos 0 |
sin 0 |
E f |
1;1 |
1;1 |
|
|
В дальнейшем, при изучении тригонометрических функций вместо аргумента чаще всего мы будем рассматривать аргумент x.
1.2. Графики тригонометрических функций
Графиком математической функции называется графическое изображение на координатной плоскости зависимости y f x , при этом каждому значению x D f соответствует ровно одно значение y. Таким образом, например, окружность, изображенная в декартовой системе координат, не является графиком.
Изобразим графики четырѐх тригонометрических функций:
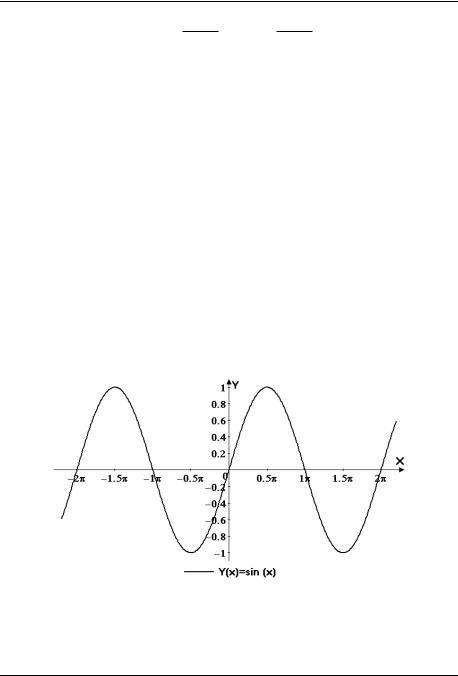
Рис. 1 y sin x
2012, ЗФТШ МФТИ, Сергеев Фѐдор Олегович
4
2012-2013 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения
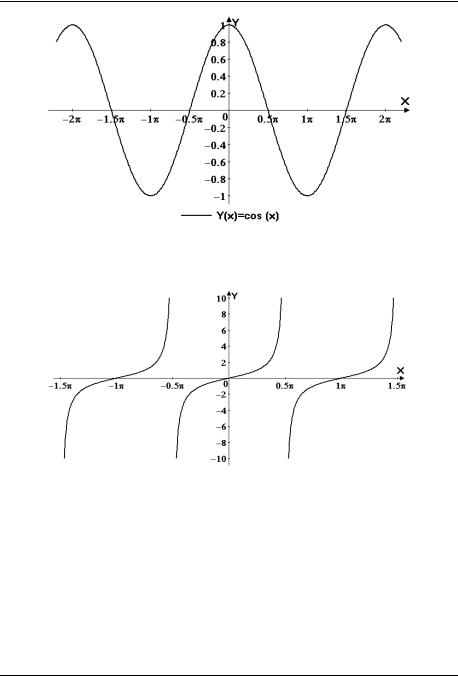
Рис. 2 y cos x
Рис. 3 y tgx
2012, ЗФТШ МФТИ, Сергеев Фѐдор Олегович
5
2012-2013 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения
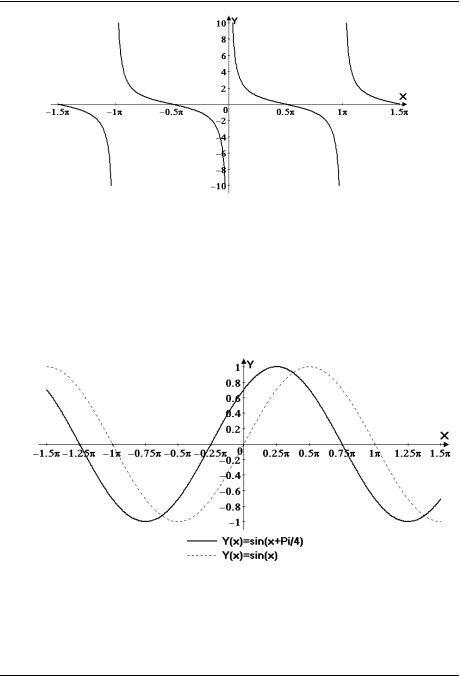
Рис. 4 y ctgx
|
|
|
|
|
Пример 1. Построить график функции y sin x |
|
. |
||
|
|
|
4 |
|
Решение. Искомый |
график получается из |
графика функции |
||
y sin x сдвигом на |
влево: |
|
|
|
4 |
|
|
|
|
Рис. 5
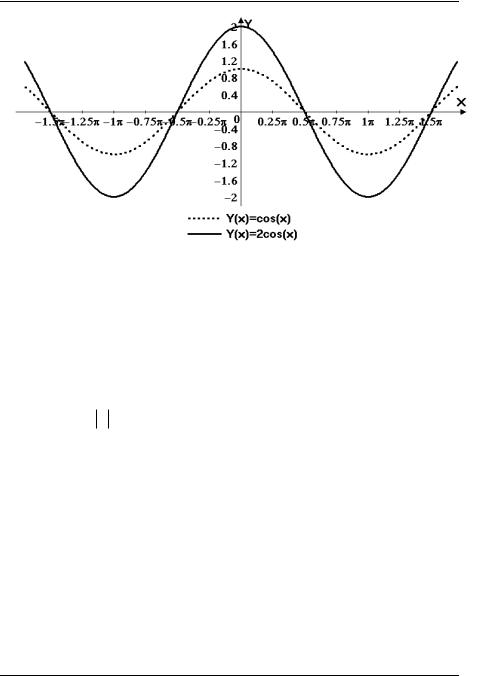
Пример 2. Построить график функции y 2 cos x.
Решение. Искомый график получается из графика функции y cos x растяжением в 2 раза по оси y.
2012, ЗФТШ МФТИ, Сергеев Фѐдор Олегович
6
2012-2013 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения
Рис. 6
1.3. Периодичность тригонометрических функций
Функция y f x называется периодической с периодом T 0, если выполняется соотношение f x T f x f x T для любого x D f при условии x T D f . При этом числа nT, n также являются периодами данной функции, если x nT D f , а число, равное T , называется еѐ основным периодом. Тригонометриче-
ские функции синуса и косинуса являются периодическими с периодом T 2 , функции тангенса и котангенса являются периодическими с
периодом T . |
|
f x |
|
|
|
|
||||
|
Примечание 1. |
Если |
– |
периодическая функция, |
T 0, то |
|||||
g x f ax b , a 0 |
также |
является |
периодической |
функцией, |
||||||
T |
|
|
T |
. |
|
|
|
|
|
|
g ( x) |
|
|
|
|
|
|
|
|||
|
|
a |
|
|
|
|
|
|
||
|
|
|
|
|
|
f x и |
g x являются периодиче- |
|||
|
Примечание 2. |
Если функции |
||||||||
скими, и при этом существуют натуральные взаимно простые числа n и m такие, что nTf mTg , то для любых ненулевых чисел a и b ли-
2012, ЗФТШ МФТИ, Сергеев Фѐдор Олегович
7

2012-2013 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения
нейная комбинация q x af x bg x |
также |
является периодиче- |
||
ской функцией, причем еѐ период T nTf |
mTg . |
|
||
Пример 3. Построить график функции y sin 2x. |
|
|||
Решение. Период функции y sin 2x |
равен |
|
2 |
. Искомый |
|
|
|||
2 |
||||
график получается «сжатием» графика y sin x в два раза по оси Х.
Рис. 7
Пример 4. Определить, является ли функция sin 2x 3 cos 3x периодической, и найти еѐ период.
Решение. Период функции sin 2x 3 |
равен T |
2 |
, период |
||||||
|
|||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n m |
2 |
; |
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
3 |
|
|
|
|
||
cos 3x равен |
. |
Получаем 3n 2m; |
Т. е., исследуемая функция |
||||||
3 |
|||||||||
|
|
n 2, m 3. |
|
|
|
||||
|
|
|
|
|
|
||||
является периодической, еѐ период T 2 .
Ответ. T 2 .
2012, ЗФТШ МФТИ, Сергеев Фѐдор Олегович
8
2012-2013 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения
1.4. Четность и нечетность тригонометрических функций
Функция y f x называется чѐтной, если выполняется условие
f x f x для любого x D f . |
Функция |
y f x называется |
|
нечѐтной, |
если выполняется условие |
f x f x для любого |
|
x D f . |
Функция косинуса является чѐтной, |
функции синуса, тан- |
|
генса и котангенса – нечѐтными.
Напомним основные свойства чѐтных и нечѐтных функций:
1)Сумма, разность и произведение двух чѐтных функций на некотором множестве является чѐтной функцией на этом множестве.
2)Сумма и разность двух нечѐтных функций на некотором множестве – нечѐтная функция на этом множестве.
3)Произведение двух нечѐтных функций на некотором множестве
– чѐтная функция на этом множестве.
4)Произведение чѐтной и нечѐтной функций на некотором множестве – нечѐтная функция на этом множестве.
Пример 5. Определить, являются ли функции чѐтными или нечѐтными
5.а. sin 2 3x cos 3x
Решение.
f x sin 2 |
3 x cos 3 x sin 3x 2 cos 3x sin 2 3x cos 3x f x . |
|||||||||||||||||||
Ответ. Функция чѐтная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.b. |
|
sin x cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
1 |
|
|
|
1 |
|
3 |
|
1 |
|
3 |
|
||||||||
|
sin x cos x |
|
|
|
|
|
sin x |
|
|
|
cos x |
|
sin x |
|
|
|
cos x. |
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
6 |
|
2 |
|
2 |
|
|
2 |
|
2 |
|
|
||
cos x – функция чѐтная, значит, |
f x также чѐтная функция. |
|
|
|
|
|||||||||||||||
Ответ. Функция четная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5.c. sin x sin 3x cos x |
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Сумма двух нечѐтных функций – нечѐтная функция, т. е. sin x sin 3x – нечѐтная функция. Произведение чѐтной и нечѐтной
2012, ЗФТШ МФТИ, Сергеев Фѐдор Олегович
9

2012-2013 уч. год, №4, 10 кл. Математика. Тригонометрические функции и уравнения
|
|
функций – нечѐтная функция, т.к. sin x sin 3x cos x |
является |
|
6 |
нечѐтной функцией. |
|
Ответ. Функция нечѐтная. |
|
5d. sin x cos x . |
|
Решение. |
|
f x sin x cos x f x . |
|
Ответ. функция не является ни чѐтной, ни нечѐтной. |
|
2. Обратные тригонометрические функции и их свойства
Напомним определение обратной функции, вводимое в курсе алгебры: функция x g y , определенная на множестве значений E f
функции y |
|
f x , |
называется обратной к этой функции, если каждо- |
||||
му элементу |
y0 E f ставится в соответствие элемент x0 такой, что |
||||||
y0 f x0 . |
|
|
|
|
|
|
|
|
Тригонометрические функции sin x, cos x,tgx, ctgx имеют обрат- |
||||||
ные – соответственно, |
arcsin x, arccos x, arctgx, arcctgx. Их свойства |
||||||
приведем в виде таблицы. |
|
||||||
|
|
|
|
|
|
||
|
f x |
|
|
arcsin x |
arccos x |
||
|
|
|
|
|
|
|
|
|
D f |
|
|
1;1 |
|
1;1 |
|
|
|
|
|
|
|
|
|
|
E f |
|
|
; |
|
0; |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Периодич- |
|
Нет |
|
Нет |
||
|
ность |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Нечѐтная |
Ни чѐтная, ни нечѐтная |
||
|
Чѐтность |
|
|
|
|
x arcsin x |
arccos x arccos x |
|
|
|
|
arcsin |
|||
|
|
|
|
|
|
|
|
2012, ЗФТШ МФТИ, Сергеев Фѐдор Олегович
10
