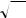
c.Число 2 – простое или четное.

d.15 делится на 5 тогда и только тогда, когда 15 делится на 3.

e.16 = -5 , но -4 ¹ (-2)2 .

f.21 £ 21.

g.Если 2× 2 = 5 , то Венера – спутник Земли.

h.Число 4 – простое, натуральное и нечетное.

1.7. Сформулировать отрицание следующих высказываний. Определить истинность полученных высказываний:

a.3+3=6.

b.2>4.

c.7 ³ 7 .

d.2×3 = 7 .

e.2 £ 2

f.(6M2) Ù (6M7) .

g.(20 > 2) Ú (3 < 7) .

h.(10 ¹ 10) Ù (14 > 11) .

i.(10 ¹ 10) Ú (14 > 11) .

j.60 делится на 6 и на 14.

k.60 делится на 6 или на 14.

l.2 – четный делитель 6.

1.8.Доказать: Ø(A Ù B) Û (ØA) Ú (ØB) (закон де Моргана).

1.9.Известно, что высказывание A Û B - истинное. Что можно сказать о следующих высказываниях:

a.ØA Û B ;

b.ØA Û ØB .

1.10.Известно, что A Þ B - истинное высказывание. Что можно сказать о высказывании ØB Þ ØA ?

1.11.Известно, что A Þ B - истинное высказывание. Что можно сказать о высказывании ØA Þ ØB ?

1.12.Известно, что A Þ B - истинное высказывание. Что можно сказать о высказывании ØA Þ B ?

2

§2 Формулы логики высказываний

2.1. Составить таблицы истинности для следующих формул логики высказываний и найти среди них тавтологии.

a.(A Þ B) Û (A Ú B) ;

b.(A Ù B) Ú C ;

c.A Ù (B Ú C) ;

d.((A Ù B) Þ C) Û (A Þ (B Þ C)) ;

e.Ø(A Þ B) Û (A Ù B) ;

f.((A Û B) Þ C) Ù A ;

g.((A Ù B) Þ C) Û (A Ú C) ;

h.(A Þ (B Ú C) ) Û (A Ù C) .

2.2. Выяснить, являются ли следующие формулы законами логики:

a.A Þ (A Þ B) ;

b.A Ù B Û A Ù B ;

c.((A Þ B) Ù B) Þ A ;

d.(A Þ B) Û (B Þ A) .

2.3. Можно ли что-нибудь сказать об истинности следующих высказываний:

a.(P Þ Q) Þ R , где R - истинное высказывание;

b.P Ù (Q Þ R) , где Q Þ R - истинное высказывание;

c.P Ú (Q Þ R) , где Q - ложное высказывание;

d.(P Ú Q) Þ (P Ù R) , где R - ложное, Q - истинное высказывание;

e.P Ú (Q Þ R) , где Q - истинное высказывание;

f.(P Ú Q) Þ (Q Ú Q) , где P - истинное высказывание;

g.(P Ú Q) Þ (Q Ù Q) ;

h.(P Þ Q) Þ (Q Þ P) , где Q - истинное высказывание;

i.(P Ú P) Û (Q Ù R) , где R - ложное высказывание.

2.4. Доказать, используя только известные Вам законы логики, что следующие формулы являются тождественно истинными:

a.(A Ù B) Ú (A Ù B) Û A ;

b.(A Ú B) Ù (A Ú B) Û A

c.(A Þ B) Ú A Û и;

d.(A Þ B) Ù A Û (A Ù B) ;

e.((A Ú B) Ù A Þ C) Û и;

f.((A Ú B) Ù A Þ C) Û (C Þ (A Ú B)) .

3

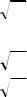
§3 Предикаты

3.1 Из следующих предложений выберите предикаты и укажите их возможное предметное множество и множество истинности:

a.2- простое число;

b.x2 − 2x −15 = 0 ;

c.для x = 5 выполняется равенство x2 − 2x −15 = 0 ;

d.число x кратно 5;

e.неверно, что число 17 кратно 5;

f.в прямоугольнике x диагонали перпендикулярны;

g.в любом прямоугольнике диагонали перпендикулярны.

3.2 Найти множество истинности для следующих предикатов:

a.x2 − 4 = 0 ;

b.x2 > 0 ;

c.(x2 − 4 = 0) (x2 −9 = 0) ;

d.x2 ≤ x ;

e.(x2 − 4 = 0) (x = 2) ;

f.x2 = −x ;

g.x2 = −1.

3.3 Запишите следующие высказывания, воспользовавшись символами кванторов (предметное множество предикатов – множество действительных чисел):

a.Всякое действительное число либо положительное, либо отрицательное, либо равно

нулю;

b.Существует наименьшее натуральное число;

c.Существует целое число, которое делиться на любое другое целое число;

d.Для любого действительного числа x верно равенство: x −9 =1;

e.Уравнение x2 − 2x −15 = 0 не имеет действительных корней;

f.Уравнение x2 + 2x − a = 0 имеет положительный корень при любом натуральном

значении a .

3.4 Задать предметное множество предиката так, чтобы на этом множестве он был общезначимым:

a.Если x делится на 3, то x - четное число.

b.Если x2 − 2x −15 = 0 , то x > 0 ;

c.Если x2 > 4 , то x > 2 ;

d.x - четное число тогда и только тогда, когда xM3;

e.x2 =1 тогда и только тогда, когда x =1;

f.x - ромб тогда и только тогда, когда диагонали x взаимно перпендикулярны;

g.x2 + 2x −1 = 0 тогда и только тогда, когда x =1;

h.x2 < 0 тогда и только тогда, когда x2 < −2 .

3.5 Пусть x - переменная, определенная на множестве N {0} . Пусть P(x) означает свойство «быть простым числом», N (x) - «быть натуральным числом», K (x) -

«быть четным числом». Запишите символически следующие высказывания и выясните их истинность:

a.существует простое четное число;

b.всякое простое число – нечетно;

c.всякое простое число – натуральное;

4

d.существуют нечетные простые числа;

e.некоторые простые числа – четные.

3.6Пусть x и y - переменные, определенные на множестве всех людей. Введем

a.Каждый человек имеет отца и мать.

b.Каждый, кто имеет отца, имеет и мать.

c.Каждый человек моложе своих родителей.

d.Существует человек, все дети которого состоят в браке.

3.7 Пусть (xn ) - бесконечная числовая последовательность и заданы следующие предикаты: P((xn )) = «в последовательности (xn ) конечное множество членов, которые не

равны нулю», Q((xn )) = «в последовательности (xn ) бесконечное множество членов,

которые равны нулю». Дать словесную формулировку и выяснить истинность следующих высказываний:

a."(xn ) (P((xn )) Þ Q((xn ))) ;

b."(xn ) (Q((xn )) Þ P((xn ))) ;

c."(xn ) (P((xn )) Û Q((xn ))) .

3.8 Выяснить, являются ли следующие предикаты выполнимыми; общезначимыми на предметном множестве R . Истинны ли следующие высказывания:

"xPi (x), $xPi (x) .

a.P1 (x) = (x > 2) ;

b.P2 (x) = (x2 + 5x + 6 = 0) ;

c.P3 (x) = ((x +1)2 = x2 + 2x +1) ;

d.P4 (x) = (x2 < -3) ;

e.P5 (x) = (x2 > 0) ;

f.P6 (x) = (x2 - 3x + 6 = 0) ;

g.P7 (x) = (sin x = 12) ;

h.P8 (x) = (x4 £ 0) ;

i.P9 (x) = (x > -3) ;

j.P10 (x) = (sin x = 2) ;

k.P11 (x) = (cos x <1) .

3.9 Выяснить, какие из следующих высказываний истинны:

a.("x Î R)("y Î R)(x2 = y2 Þ x = y) ;

b.("x Î R)("y Î R)(x = y Þ x2 = y2 ) ;

c.("x Î R)($y Î R)(x2 = y2 Þ x = y) ;

d.("x Î R)("y Î R)((xy > 0 Ù y > 0) Þ x > 0) ;

e.("x Î Z )("y Î Z)($z Î Z )(x × y = z) ;

f.("x Î Z )($z Î Z )("y Î Z )(x × y = z) ;

g.($x Î Z)($z Î Z )("y Î Z )(x × y = z) ;

h.($x Î Z)("y Î Z)($z Î Z )(x × y = z) ;

i.("x Î Z )("z Î Z )($y Î Z )(x × y = z) .

5

3.10Является ли высказывание «Ни одна планета не светит отраженным светом» отрицанием высказывания «Все планеты светят отраженным светом»?

3.11Сформулировать отрицание высказываний и определить истинность полученных высказываний. x определен на множестве R.

a. Все студенты математического факультета моложе 100 лет.

b.$x(x2 > -5) ;

c."x(x2 £ -5) ;

d."x(sin x > 12) ;

e.$x(2x > 2) ;

f.$x(x2 £ 0) ;

g."x(æ 1 öx > 0) ; çè 2 ÷ø

h.$x(sin x = 1) ;

i."x( x > 0) ;

j.$x(x2 + x +1 = 0) ;

k."x((x > 3) Ú (x £ 5)) ;

l."x((x < 5) Ù (x = 9)) ;

m.$x((x < 5) Ù (x = 9)) ;

n.$x((sin x > 2) Ù (x2 < 5)) ;

o."x((x = 2) Ú (xM7)) .

3.12 Свяжите переменную квантором так, чтобы получить истинное высказывание (переменная x R ).

a.x = -x ;

b.x2 ³ 0 ;

c.x2 + 2 £ 0 ;

d.sin x ¹ 2 ;

e.æ 1 öx ³ 0 . çè 2 ÷ø

3.13 В следующих предложениях вместо многоточия поставьте слова «необходимо», «достаточно» или «необходимо и достаточно» так, чтобы получились истинные высказывания. Ответ обоснуйте.

a.Для того чтобы стороны четырехугольника были равны, ... чтобы он был квадратом.

b.Для того чтобы квадрат числа был меньше 100, ... чтобы число было меньше 10.

c.Для того чтобы площадь прямоугольника была равна 4 см2, ... чтобы длины обеих его сторон были равны 2 см.

d.Для того чтобы разность двух целых чисел была четной, ... чтобы эти числа имели одинаковую четность.

e.Для того чтобы одно из целых чисел было кратно 6, а другое – кратно 4, ... чтобы их произведение было кратно 12.

f.Для того чтобы целое число было кратно 4 и кратно 15, ... чтобы оно было кратно

60.

g.Для того, чтобы произведение двух целых чисел было кратно 11, ... чтобы оба сомножителя были кратны 11.

h.Для того чтобы у параллелограмма диагонали были равны, ... чтобы он был квадратом.

6

i.Для того чтобы сумма двух целых чисел делилась на целое число с, … чтобы каждое слагаемое делилось на с.

j.Для того чтобы медиана треугольника была равна половине стороны, которую она делит пополам, … чтобы треугольник был прямоугольным.

k.Для того чтобы треугольник был прямоугольным, … чтобы один из его углов был равен сумме двух других углов.

3.14По определению, подмножество X множества R называется ограниченным сверху, если существует такое действительное число M , что для всех элементов x множества X x ≤ M . Сформулируйте утверждение, что множество X R не является ограниченным сверху.

3.15Пусть X - непустое подмножество множества R. Действительное число m0

называется нижней границей подмножества X R , если при всех x X m0 ≤ x .

Сформулируйте утверждение, что действительное число m не является нижней границей множества X R .

3.16 Бесконечная числовая последовательность (an ) называется монотонно возрастающей, если n an+1 > an . Сформулируйте утверждение, что последовательность (an ) не является монотонно возрастающей.

3.17 Бесконечная числовая последовательность (an ) называется невозрастающей, если n an+1 ≤ an . Сформулируйте утверждение, что последовательность (an ) не является

невозрастающей. Верно ли, что если последовательность не является возрастающей, то она является невозрастающей?

7