Лабораторна робота №4
Тема: ЧИСЛА, КОДУВАННЯ Й АРИФМЕТИЧНА ІНФОРМАЦІЯ
Ціль роботи: Вивчення способів організації й дослідження програм виконання арифметичних операцій, програмування мовою Асемблера й машинній мові.
Теоретична частина двйково-десяткові числа
З метою зручності перетворення чисті двійкові числа представляються десятковими або шістнадцятковими. Однак двоїчно-десяткове перетворення - операція не проста. У калькуляторах, магістралях і числових приладах, коли на доступних користувачеві виходах і входах широко поширені десяткові числа, для їхнього подання використовують спеціальний двоїчно-десятковий код (ДДК). У табл. 1 наведено кілька десяткових чисел і відповідних їм двійково-десяткових еквівалентів (система 8421). Цим визначаються ваги позицій кожного із чотирьох біт ДДК (використовують інші ДДК, наприклад 5421 і плюс 3).
Таблиця 1. Двійково-десятковий код 8421
-
Десяткові числа
Двійково-десяткові числа
8
4
2
1
0
1
2
3
4
5
6
7
8
9
0
0
0
0
0
0
0
0
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
0
1
0
1
0
1
0
1
0
1
Запишемо десяткове число 3691 у ДДК 8421. Кожна десяткова цифра перетвориться прямо у свій двоїчно-десятковий еквівалент із 4 біт, і перетворення дають 369110 = 11 0110 1001 0001ДДК:
Десяткове число 3 6 9 1
Двійково-десяткове число 0011 0110 1001 0001
Перетворимо тепер двійково-десяткове число 1000 0000 0111 0010 у його десятковий еквівалент. Кожна група з 4 біт прямо перетвориться в її десятковий еквівалент, і тоді одержуємо 1000 0000 0111 0010ддк = 807210:
Двійково-десяткове число 1000 0000 0111 0010
Десяткове число 8 0 7 2
Мікропроцесори складають чисті двійкові числа, але вони володіють, однак, командами для перетворення результату своїх додавань у двійково-десятковий запис. Отримані двоїчно-десяткові числа легко потім представити в десятковому записі, використовуючи вище описані прості процедури.
Вправи
1. Запис ДДК є скороченням _______________.
2. Найбільш загальним записом двійково-десяткового коду є ДДК ____ (5421, 8421).
3. Записати наступні десяткові числа в ДДК 8421: а) 39; б) 65; в) 40; г) 17; д) 82; е) 99.
4. Записати наступні двійково-десяткові числа в десятковому коді: а) 1000 0000; б) 0000 0001; в) 1001 0010; г) 0111 0110; д) 0100 0011; е) 0101 0101.
Двійкова арифметика
Додавання, вирахування або множення двійкових чисел виконуються так само, як і в арифметиці десяткових чисел. Більшість мікропроцесорів володіє командами додавання й вирахування двійкових чисел, однак деякі, менш численні виконують команди множення й розподілу (наприклад, мікропроцесори Intel 8086 Intel 8088).
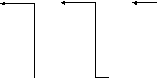
На мал. 1,а представлені прості правила двійкового додавання. Два перших (ліворуч) правила очевидні, третє показує, що 1 + 1 = 10, тобто найбільш значима 1 переноситься в найближчий старший розряд. Четверте правило, нарешті, показує, що 1 + 1 + 1 = 11. У цьому випадку перший, другий доданки й доданок, що запам'ятовується в результаті додавання в молодшому розряді число - всі 1. Результатом є сума - 1 з переносом 1.
|
|
|
|
1 |
1 |
|
|
1 – й доданок |
0 |
0 |
1 |
1 |
запам’ятову-вання з менш значимої позиції
а) |
|
|
+ |
+ |
+ |
+ | |
|
2 – й доданок |
0 |
1 |
1 |
1 | |
|
Сума |
0 |
1 |
10 |
11 | |
|
|
|
|
перенесення |
перенесення | |
|
|
|
|
до іншого старшого розряду | ||
1
-
111 1
перенесення
1
1 – й доданок
00111011
59
+
+
2 – й доданок
00101010
42
Сума
011001012
10110
б)
Рис 1. Правила двійкового додавання а) правила, б) приклад
Складемо двійкові числа 0011 1011 і 0010 1010 (операція показана на мал. 1,б). Для більшої ясності дії з десятковими еквівалентами оброблюваних чисел показані на малюнку праворуч. Сумою двох чисел 0011 1011 і 0010 1010 буде 0110 01012.
На мал. 2,а наведені правила двійкового вирахування. Перші три аналогічні десятковому вирахуванню. Останнє вимагає позики з більш значимого попереднього розряду (у цьому випадку вага 2). Зменшуваним є двійкове число 10, що віднімається 1, різницею - 1.
Віднімемо двійкове число 0011 1001 з 0101 0101. Цей приклад наведений на мал. 2.,б. Розряди ваг 1, 2 і 4 ці двійкові вирахування прості для виконання й ставляться до першого трьох правилам на мал. 2.,а. У колонку ваги 8 має місце вирахування 1 з 0. Тоді 1 позичається з колонки ваги 16.
|
|
|
|
|
0 |
|
|
|
|
|
|
|
10 |
0 10 0 10 |
|
|
зменшуване |
0 |
1 |
1 |
10 |
0 1 0 1 0 1 0 1 |
85 |
|
|
- |
- |
- |
- |
- |
- |
|
від’ємник |
0 |
0 |
1 |
1 |
0 0 1 1 1 0 0 1 |
57 |
|
різниця |
0 |
1 |
0 |
1 |
0 0 0 1 1 1 0 02 |
2810 |
|
|
а) |
б) | ||||
1 10
Рис 2. Правила двійкового віднімання а) правила, б)приклад
Одиниця віднімається з 102, що дає різницю 1 відповідно до четвертого правила на мал. 2,а. Після цієї позики в колонці ваги 16 має місце вирахування 1 з нового від’ємника 0. Відповідно до четвертого правила 1 повинна бути зайнята з наступної, більше значимої позиції (колонка ваги 32), але в колонку 32 маємо 0; тому колонка 32 повинна зробити позику з колонки ваги 64, що й виконано. Остаточно колонка 16 робить позику з колонки 32, зменшуваним у колонку 16 стає 102, від’ємника 1, різницею 1. У колонку 32 маємо 1 – 1 = 0, у колонку 64 – 0 – 0 = 0, у колонку 128 — 0 – 0 = 0. Таким чином, мал. 2.5,б ілюструє операцію вирахування 0011 10012 з 0101 01012 (праворуч це завдання вирішене в десятковому записі).
Приведемо правила десяткового множення:
Множник 0 1 0 1
* * * *
Множник 0 0 1 1
Добуток 0 0 0 1
Два перші правила не вимагають ніяких пояснень. У двох наступним множником є 1: коли множником є 1 при двійковому множенні, множене стає результатом і являє собою добуток. Коли множник 0, добуток завжди 0.
Виконаємо множення 1101 на 101. Як і у випадку множення десяткових чисел, множене спочатку множиться на число, що знаходиться в молодшому розряді (у розглянутому випадку - біт у колонку ваги 1).
Множене 1101 13
* *
Множник 101 5
1-й частковий добуток 1101 6510
2-й частковий добуток 0000
3-й частковий добуток 1101
Кінцевий добуток 10000012
Оскільки біт множника в розряді ваги 1 є 1, множене копіюється й становить перший частковий добуток. Другим бітом множника є 0, тоді другий частковий добуток є 0000 (помітимо, що воно зрушено на одну позицію вліво). Бытом розряду ваги 4 множники є 1, тоді для одержання третього часткового добутку знову треба копіювати множник (помітимо, що копіювання завершується новим зрушенням на одну позицію вліво). Після цього виконуємо додавання трьох часткових добутків, що дає результат 10000012. Отриманий результат 11012 × 1012 = 10000012 відповідає добутку десяткових чисел 1310 × × 510 = 6510.
Вправи
1. Виконати наступні додавання двійкових чисел:
а) 1010 6) 1101 в) 0101 1011 г) 0011 1111
+ + + +
0101 0101 0000 1111 0001 1111.
2. Виконати наступні вирахування двійкових чисел:
а) 1110 6) 1010 в) 0110 0110 г) 0111 1000
- - - -
1000 0101 0001 1010 0011 1111.
3. Перше число при множенні називається ________, друге - множником, а результат становить _________.
4. Виконати наступні множення двійкових чисел:
а) 1001 б) 1101 в) 1111 г) 1110
× × × ×
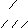11 1001 101 1110.