Т(критерий подгрупп)

Н подгр-па G 

1.Н замкнуто относит-но опрераций + и *

2.н.э. , где е- н.э. в G

3.

Пр-р: <Z,+> - гр., <H,+> - подгр., где H – мн-во чисел кратных 3.

Опр. Группа

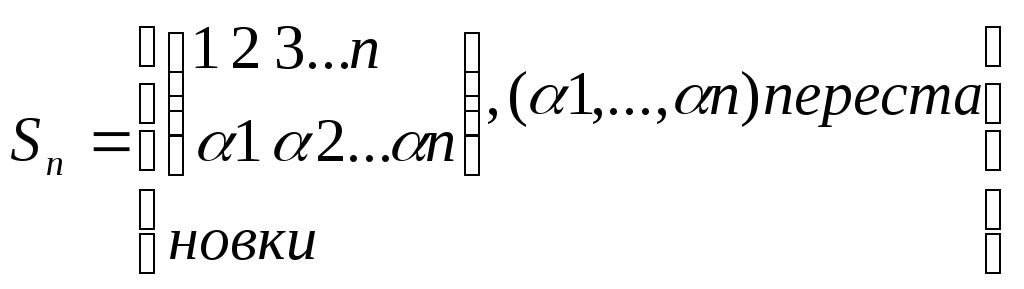
наз-ся симметрической.

Теор Кэли. Всякая конечная группа порядка n изоморфна некоторой подгр. симметрической гр. S_n n-го порядка.

Д-во: Пусть T(G)-совок-ть всех левых трансляций мн-ва G. По теор (предыдущей) есть подгруппа группы S_G.

Пусть h- отображение мн-ва G на T(G), определяемое формулой

. H сохр. главные операции группы I.

h-инъект. отобр., т.к. , если h(a)=h(b), то t_a=t_b, t_a(l)=t_b(e), где e- единица группы I, ae=be, значит a=b. След-но h- изоморфизм группы I на подгруппу F сим-ой группы S_G на мн-во G. Ч.т.д.

Опр. Эл-т aG наз-ся эл-том конечного порядка, если для него найдется нат-е число n такое, что aⁿ=e (единичному эл-ту группы). Если для эл-та a гр. G такого нат-го числа n не сущ-ет, то эл-т a наз-ся эл-том бескон-го порядка.

Опр. Порядком эл-та a группы G наз-ся наименьшее нат-е число k такое, что a^k=e. Обознач-ся О(а).

Теор. В конечн. гр. <G,·> всякий эл-т имеет конечный порядок.

Теор. Если порядок эл-та а равен k и эл-т b имеет вид a^s, то порядок эл-та a^s равен k/НОД(s,k).

Опр. Пусть G=(a). Такая группа наз-ся циклической с порождающим элементом а.

Теор. Любая бесконечная циклическая группа изоморфна группе целых чисел по сложению. Любая конечная циклическая группа порядка n изоморфна группе остатков от деления на n.

Теор. Любая подгруппа циклической группы – циклическая.

Смежные классы группы по подгруппе.

Опр. Дана группа G. Н-подгруппа G, -фиксированный=> левым смежным классом, порожд.эл-ом а наз-ся множ-во ,кот.состоит из

Правм смежным классом, порожд.эл-ом а наз-ся множ-во

Св-ва:

1. Любые два правых смежных класса гр. G по подгр. Н либо совпадают, либо не пересекаются.

2. Пусть K – конечная подгр.гр. G, gG. Тогда число эл-тов смеж-го класса Hg равно числу эл-тов мн-ва H.

Опр Пусть G – конечная гр. Число эл-тов ее основного мн-ва G наз-ся порядком гр. G.

Теор Лагранжа. Порядок подгр. конечной гр. яв-ся делителем порядка гр.

Док-во. Пусть K – подгр. конечной гр. G и H, Hg₂, …, Hg_k – мн-во всех различных правых смежных классов гр. G по подгр. K. Тогда G=H  Hg₂ ... Hg_k (1), причем любые два смежных класса, входящих в это объед-е, не пересекаются. Поэтому если n – число эл-тов мн-ва G и m – число эл-тов мн-ва H, то, по свойству 4, число эл-тов любого смежного класса Hg_i равно m и в силу (1) n=mk.

Сл-е 1. Если G – конечная гр. порядка n и gG, то порядок эл-та g делит n.

Сл-е 2. Любая конечная гр. простого порядка яв-ся циклической.

Опр. Алгебра наз кольцом,е/и вып. след.усл-я:

0) К замкнуто относ-но + и *

1. <K,+> - алгебраическая система – коммутативная или абелева гр:

а) (a,bK)(a+b=b+a) (ab=ba)

б)(a,b,cK) ((a+b)+c=a+(b+c))

в) ( 0K)(aK)(a+0=a)

(1 K)(aK)(a*1=a)

г) (aK)( -aK)(a+(-a)=0) (aK)( K)(a*=1)

2) Операция умнож-я в K ассоциативна, т.е. (a,b,cK)((ab)c=a(bc))

3) Сложение связано двумя законами дистрибутивности:

a, b, cK (a(b+c)=ab+ac) и ((a+b)c=ac+bc)

Пр-ры:Z, 2Z,Q, R, Z[i]={a+bi/a,b Z} – кольца, N – не кольцо.

Св-ва колец.

1. Т. к. <K,+> - группа, то в K нулевой эл-т единственный.

2. Для каждого эл-та противоположный тоже единственный.

3. Ур-ние вида a+x=b имеет единственный корень (a, bK). Очевидно, корнем будет x=b+(-a), b+(-a)=b-a – так будем обозначать и наз-ть разностью эл-тов b и a.

4. Операция вычитания связана с операцией умножения двумя законами дистрибутивности: (a-b)c=ac-bc ; c(a-b)=ca-cb.

5. Для любого aK a·0=0 (a·0=a(b-b)=ab-ab=0).

6. a(-b)=-(ab) ( ab+a(-b)=a(b+(-b))=a·0=0 ) ; -a(-b)=ab ( -a(-b)=-(-ab)=ab )

Опр. Непустое подмн-во H кольца K наз-ся подкольцом кольца K, если H яв-ся кольцом относ-но операций, определенных в K.

Пр-р. <Z,+,·> - кольцо. Мн-во четн чисел – подкольцо в кольце Z.

Теор (критерий подкольца). Непустое подмн-во H кольца K яв-ся подкольцом в K, если мн-во H замкнуто относ-но операции вычитания и умножения.

Область целостности.

Опр. Кольцо K наз-ся коммутативным, если операция умнож-я в нем коммутативна, т. е. a,bK (ab=ba).

Опр. Кольцо K наз-ся кольцом с единицей, если K содержит нейтральный эл-т (единичный) относительно операции умножения.

Опр. Эл-т a≠0 из K наз-ся делителем нуля, если в K найдется эл-т b≠0 такой, что ab=0 или ba=0.

Опр. Коммутативное кольцо с единицей, в к-ром нет делителей нуля, наз-ся областью целостности.

Делимость в кольце.

Будем рассматривать коммутативные кольца с единицей.

Опр. Эл-т а из кольца делится на эл-т b из K, если a=bq при нек-ром q из K.

Отнош-е делимости в K обладает всеми св-ми, к-рыми это отнош-е обладает в кольце Z. ( РФ: аа ; любое а1 и а(-1) ; ab и bс, то ac ; ab и cb, то (a±c)b ; ac то abc ; ab то |a|≥|b| ; ab и ba то a=b или a=-b )

Опр. Разделить целое число а на целое число b≠0 с остатком, значит найти целые числа q и r такие, что выполняются условия: a=bq+r; 0≤r<|b|.

Т. Всякое целое число a можно разделить с остатком на целое число b≠0 и притом единственным образом.

Т. В области целостности из равенства ab=ac, где a, b, c принадлежат области целостности K и а≠0, следует b=c.

Док-во. ab=ac, ab-ac=0, a(b-c)=0, b-c=0, b=c.

Опр. Эл-т a’K наз-ся обратным для aK, если aa’=a’a=e.

Опр. Если эл-т aK имеет обратный a’K, то эл-т а наз-ся обратимым в K.

Т. Мн-во K^* всех обратимых эл-тов кольца K образует группу относительно операции умножения.

Док-во. Докажем, что <K^*,·> - группа.

1. Пусть a, bK^*. Докажем, что abK^*. Т. к. a, bK^*, то a, a^-1, b, b^-1

abb^-1a^-1=a(bb^-1)a^-1=aea^-1=aa^-1=e, т. е. ab K^*.

2. eK^*.

3. Умножение в K^* ассоциативно: a, b, cK^* ((ab)c=a(bc))

4. Если аK^*, то для него сущ-ет ему обратный в K^*. Т. к. аK^*, то для него обратный есть – это а^-1K^*. Ч. Т. Д.

Опр. К-область целостности. a,b K.Элементы a,b наз-ся ассоциированными, если они отлич-ся на обратимый эл-т

a,b-ассоц

Опр К-область целостности. Ненул эл-т a наз-ся простым, е/и он необратим в К и из рав-ва a=bc следует, что и(или с)обратим

Опр. Эл-т а≠0 из области целостности K наз-ся составным, если он необратим и допускает предстваление в виде: a=bc,где b.c –необратимы и b,с K

Опр. Коммутативное кольцо, в котором не менее двух эл-тов и всякий ненулевой эл-т которого обратим, наз-ся полем.

Опр. Подполем поля F наз-ся подкольцо поля F, в к-ром всякий ненулевой эл-т обратим.

Св-ва поля: Пусть F=<F,+,-,*,1> - поле. Тогда для любых эл-тов a,b,c поля :

1. если ab=1,то a<>0 и b=a^-1; 2. если ac=bc и c<>0, то a=b; 3. если ab=0,то a=0 или b=0; 4. если a<>0 и b<>0, то ab<>0; 5. a/b=c/d т. и т.т., когда ad=bc, b<>0 и d<>0;

6. a/b+-c/d=(ad+-bc)/(bd);

7. a/b*c/d=(ac)/(bd); 8.

a/b+(-a)/b=0 и –(a/b)=(-a)/b;

9. если a<>0 и b<>0, то

(a/b)^-1=b/a

10. ac/bc= a/b

М6,7 - 6. Кольцо мн-нов от одной переменной.

Опр. Выражение вида наз-ся многочленом с коэф-ми из К (кольцо), ai из K.

Опр. Два многочлена наз-ся равными, если они имеют одинаковые соотв-е коэф-ты.

Если в записи

а_n<>0, то многочлен f имеет степень n.

Операции

Если f(x)= a₀+a₁x+a₂x²+…+a_nxⁿ, g(x)=b₀+b₁x+b₂x²+…+b_kx^k,то f+g=(a₀+b₀)+…+(a_p+b_p)x^p, где p=max(n,k). Произведением многочленов f и g назыв. сумма всевозмож. произведений U и V,где U-любой член f,V-любой член g.

Теор: Относительно операций + *- многочлены с коэф-ми из К образуют кольцо. Обознач К[x].

Теор: (Схема Горнера) Пусть f(x) мн-н из K[x], тогда для любого х₀К мн-н f(x) можно единственным образом представить в виде f(x)=g(x)(x-x₀)+c (*), где

Опр.: Эл-т х₀кольца К называется корнем f(x) из K[x], если f(x₀)=0

Теор (Безу) мн-н f(x) делится на (х-х₀) в кольце K[x] , т.и.т.т.к. х₀явл-ся его корнем.

док-во: => f(x) делится на (х-х0), тогда f(x)=h(x)(x-х0), след-но, х0 – корень. <= пусть f(x0)=0. f(x) делится с остатком на h(x) (по т. горнера) Тогда f(x)=h(x)(x-a). Чтд

теор. Число корней не нулевого мн-на не превосходит его степени.

Теор (о делении с остатком) пусть Р- произв-е поле, f(x) и g(x) мн-ны Р[x], причем g(x)0, тогда ! пара мн-нов g(x) и r(x) Р[x], такая что

1. f(x)= g(x)q+ r(x)

2. deg r(x) < deg g(x)

Док-во: Пусть f(x)= , g(x)=, причем а₀≠0 и b₀≠0, если n<m. то можем взять g(x)=0, а r(x)=f(x), тогда f(x)=0*q+r(x). Пусть n>=m. Тогда введем новый мн-н

f₁ (x)= f(x)-с₀x^n-m*g(x), с₀=а₀/b₀

Deg f₁ (x) <n-1. Пусть f₁(x) имеет стандартный вид f₁ (x)=. Положим f₂(x)= f(x)-с₁x^n-m-1*g(x), где с₁=а₀/b₀ тогда deg f₂(x) <=n-2

Продолжая этот процесс, получим послед-ть мн-нов f₁(x),.., f_n(x), причем deg f_k(x)<=n-k. Последним получим мн-н

f_n-m-1(x), степень кот-го <степени мн-на g(x)

f_n-m-1(x)=. Отсюда f(x)= + f_n-m-1(x), получаем g(x)= единс-ть: Предположим противное f(x)=q₁ g(x)+r₁=q₂ g(x)+r₂, deg r₂ < deg g(x), deg r₁ < g(x). Рассмотрим разность (q₁-q₂) g(x)=r₂-r₁, если q₁ ≠q₂ deg(q₁-q₂)g>= deg g(x), но степень r₂-r₁ , deg g(x) противоречие q₁=q₂ r₁=r₂

НОД мн-нов над полем

если мн-н D обладает св-ми:

1. D яв-ся делителем каждого из мн-нов f₁(x) … f_n(x) т.е.их общим делителем.

2. D делится на всякий ОД мн-нов f₁(x) … f_n(x) наз-ся НОД мн-нов f₁(x) … f_n(x)

Теор НОД ! и можно представить его в виде D= u₁*f₁(x)+ … +u_nf_n(x), где u_i Р[x]

Опр Представление к-либо мн-на в этом виде наз-ся его линейным представлением.

Зам: НОД мн-нов f₁(x) … f_n(x) м.б. определен как их общий делитель наиб-й степени

Алгоритм Евклида:

НОД двух мн-нов f (x) и g(x) Р[x] можно найти при помощи алгоритма Евклида

f=gq₁+r₁, g=q₂r₁+r₂…. r_n-2=q_nr_n-1+r_n,

r_n-1=q_n+1r_n

Причем degr_n<degr₂ <.. <deg g последний ненулевой остаток r_n это и есть НОД мн-нов g и f. НОД неск-х мн-нов м.б. найден индуктивным способом. Делители мн-на НОД(f₁(x) … f_n(x)) это в точности делители мн-нов f₁(x) … f_n(x)

Линейное представ-е НОД мн-нов

Пусть D НОД мн-нов f и g P[x], тогда всякий h кратный D можно представить в виде uf+vg,где u и vP[x], это наз-ся линейным представлением числа. 2 способа представления:

1.При помощи алгоритма Евклида (Каждое последующее равенство подставляем в предыдущее).

2.Метод неопр-х коэф-в: т.к. h кратно D, то h=h₁ D=h₁uf+h₁vg. Запишем искомые мн-ны u и v в общем виде с неопр-ми коэф-ми. Тогда приравнивая коэф-ты при одинаковых степенях х в рав-ве, получим сис-му ЛУ для применения этого метода необх-мо знать оценки степеней u и v. чтобы знать, в каком виде их запомнить.

Взаимно-простые мн-ны:

Опр. Мн-ны f₁(x) … f_n(x) называются взаимнопростыми, если выполняется НОД(f₁(x) … f_n(x))=1

Теор Мн-ны f₁(x) … f_n(x) P[x] взаимопросты↔ такие мн-ены P[x], что 1 линейно выражается через f₁(x) … f_n(x)т.е. 1=

Док-во: пусть f₁(x) … f_n(x) взаимнопросты . тогда НОД(f₁(x) … f_n(x))=1 =1

обратно: Пусть выполняется условие =1, тогда всякий делитель f₁(x) … f_n(x) будет делить левую часть равенства. делить ед-цу он ассоциирован с 1 яв-ся эл-том Р. чтд.

Любой мн-н м.б. представлен в виде = h, если f₁(x) … f_n(x) взаимопросты.

НОК мн-нов:

НОК мн-нов f₁(x) … f_n(x) наз-ся мн-н h облад-ий свойствами:

1.мн-н h делится на мн-ны f₁(x) … f_n(x), т.е. яв-ся их общим кратным.

2. h делит любое общее кратное мн-нов f₁(x) … f_n(x)

Теор НОК !

Теор Для двух мн-нов f и g НОК(f,g) и НОД(f,g) связаны соотношением НОК(f,g)* НОД(f,g)=с f g, где с –некоторый эл-т P[x].

Разложение мн-нов на неприводимые множители:

Опр: Ненулевой эл-т наз-ся простым, если он не обратим и не м.б. разложен в произведение двух необратимых эл-тов. Простые эл-ты кольца P[x], наз-ся неприводимыми мн-нами. (это такой мн-н. положит-е степени к-го м.б. представлены в виде двух мн-нов меньшей степени.)

Пр-ры: ax+b, a<>0 не приводим над любым полем.

2. x²-2=(x-√2)(x+√2) не приводим над U, но приводим над R.

Теор: Всякий мн-н fP[x], не явл. эл-том поля Р, м.б.разложен в произведение неприводимых множителей f=р₁р₂.. р_n, причем если f= q₁q₂.. q_l,-другое разложение на неприводимые множители, то m=l и

М6,7 - 7. Элементы теории срав-ий

Опр. Пусть m N, m>1, a,bZ. Число a сравнимо с числом b по модулю m, если (a-b)m a≡b(mod m)  (a-b)m.

Т (признак сравнимости): Целые числа a и b сравнимы по модулю m  они при дел-ии на m дают одинаковые остатки. a≡b(mod m) rest (a,m)= rest(b,m)

Опр.Два целых числа a и b наз. срав-ми по мод. M, если при дел-ии на m они дают один-е остатки.

След. Всякое целое число сравнимо по мод. m с остатком от дел-ия этого числа на m, т.е. если a=mq+r, где , то a=r(mod m)

Св-ва (несвязанные с модулем):

1)Отношение срав-ия на Z явл. oтношением эквив-ти (очевидно).

2)Верные срав-я по одному и тому же модулю можно почленно складывать и вычитать.

3)Срав-ия по одному и тому же модулю можно почленно умножать.

Сл-е: а) к обеим частям верного срав-ия можно прибавлять любое целое число

б) члены срав-ия можно переносить из одной части в другую с противоположным знаком

в) обе части срав-ия можно возводить в любую натуральную степень

г) обе части срав-ия можно умножать на любое целое число

д) пусть f(x) – мн-н с целыми коэфф. f(x)=a₀+a₁x¹+…+a_nxⁿ, где a_iZ,i=0,…,n Если c≡d(mod m), то f(c)≡f(d)(mod m).

Св-ва (связанные с модулем)

1)Если два числа сравнимы по mod m, то они срав-мы по любому делителю этого модуля.

2)Обе части срав-ия и mod можно сократить на их общий множитель.

3)Обе части срав-ия и mod можно умножить на любое целое число >1.

4)Обе части срав-ия можно разделить на число, вз-о простое с mod, если это число делит каждую из частей срав-ия.

Отнош-е сравн-ти на Z явл. отнош-м эквив-ти. Мн Z при этом разбивается на непустые, непересек-ся классы эквив-ти, к-ые в объединении состав. всё мн-во целых чисел. Это классы сравнимых между собой чисел по данному модулю.

ОПР. Классы эквивал. по отношению сравн-ти наз-т классами вычетов. Эл-ты этих классов наз-т вычетами.

Обознач: aZ, - класс вычетов, порождённый элем-м а. ={xZ /x≡a (mod m)}.

Т: Сущ-ет ровно m различных классов вычетов по mod m.

Все классы по модулю m обознач (, ,… , ). Мн-во всех классов вычетов по модулю m обознач Z_m ={,, … , } – фактор – мн-во.

Опр Суммой кл выч и называется класс, порождённый эл-м .

+=, анал-но произведение.

Т: <Z_m ,+,*> - кольцо

Рас-м Z_m =={,,… , }. Выберем по одному эл-ту из каждого класса вычетов. Получим полную систему вычетов (ПСВ).

ОПР. ПСВ по mod m наз-ся совок-ть чисел, взятых в точности по одному из каждого класса вычетов по данному mod. Из опр. ═> а)ПСВ_m содержит ровно m эл-ов.б) т.к. каждый класс – бескон-е мн-во, то ясно, что ПСВ бесконечно много, среди них выдел. нес-ко особых, н-р, Z_{5 , , …,}

ПСВ₅ – 5, 1, 42, 3, -1

Т: Любая совок-ть m - различных чисел образует ПСВ_m тогда и только тогда, когда они попарно несрав-мы.

Т: Пусть НОД(a,m)=1,a,bZ. x₁,x₂, …, x_m – ПСВ. Док-ть: ax₁+b, ax₂+b, …, ax_m+b – ПСВ.

Согласно предыдущей теореме достаточно доказать, что данные числа попарно несравнимы (МПО).

Приведённые системы вычетов – особое подмн-во ПСВ.

ОПР. Пусть Z_m =={,,… , }, Z_m. НОД класса и mod m наз-т НОД представителя этого класса и модуля: НОД(,m)=НОД(a,m)

ОПР.Кл выч наз-т взаимно простым с модулем m, если НОД(,m)=1.

Если из каждого класса вычетов, взаимно простого с модулем, взять в точности по одному элементу, то получ. Приведенную СВ.

ОПР. Привед.СВ назыв. совок-ть чисел, взятых в точности по одному из каждого класса, вз-о простого с модулем, и попарно несравнимых.

Пр-р. Z₅ ={_{, , …,} } НОД(_, )=НОД(0,5)=5 ПрСВ наим. полож. 1,2,3,4. ПрСВ абсол. Наим. 1,2,-2,-1.

Т. Пусть в Z_m имеется ровно к-классов взаим. простых с mod m , тогда любая совок-ть к-чисел попарно несравнимых по mod m и взаим. простых с mod m явл. ПрСВ.

Т: Если НОД(a,m)=1 и x₁,x₂, …, x_m – Пр.СВ, то ax₁, ax₂, …, ax_m – Пр.СВ.

Дост-но д-ть, что числа ax₁, ax₂, …, ax_m – попарно несравнимы и взаим. простых с mod m.

Функция Эйлера.

Пусть m- произ. натур. число. Поставим в соот. числу m кол-во N чисел, не превосход. m и взаим. простых с ним (ф-ция Эйлера фи(n)).

Т.о. задана ф-я Эйлера: φ:N→N.

Пр: N, φ(8)=4, 7 N, φ(7)=6.

Пред-е: кол-во эл-ов в любой Пр.СВ по mod m= φ(m)

Лемма : а)Если p- простое, то φ(p)=p-1. б) φ(p^k)= p^k-1 (p-1)

ОПР. Ф-я назыв. мультипликативной, если cохран. oперацию умнож. f(a*b)=f(a)*f(b), если (a,b)=1.

Функция Эйлера – мультипликатив.

Т.Эйлера: Если числа (a,m)=1, то a^φ(m) ≡1(mod m)

Д-во: Рассм. Пр.СВ по mod m наим. полож. Пусть Пр.СВ (наим. полож) состоит из чисел x₁,x₂, …, x_φ(m).

Построим ещё одну Пр.СВ, домножив x_i на a: ax₁, ax₂, …, ax_φ(m) . Заменим каждый вычет наим. положительным. Пусть, нп, 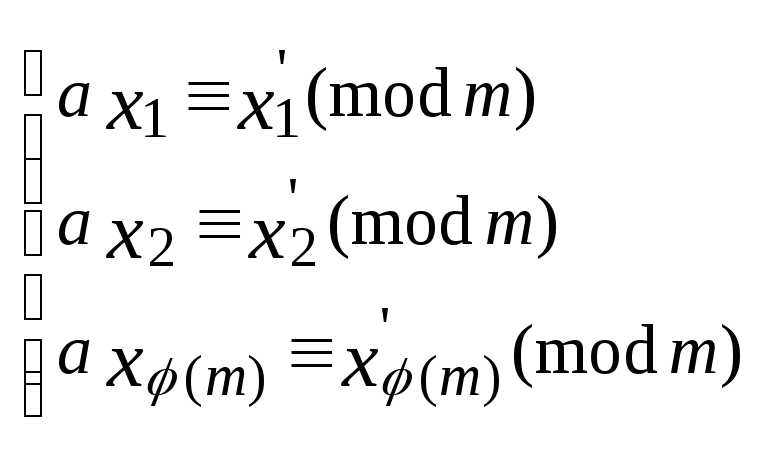, где x_i^΄ – наим. полож. вычет соот. класса.

Перемножим почленно все равные системы (*): (**) a^φ(m) *x₁*x₂*…* x_φ(m) ≡x₁^΄ *x₂^΄ *…* x_φ(m)^΄ (mod m).

Заметим, что x₁^΄ ,x₂^΄ , …, x_φ(m)^΄ - Пр.СВ (наим. полож), т.е. множество { x₁,x₂, …, x_φ(m) } совпадает со множеством { x₁^΄ ,x₂^΄ ,…, x_φ(m)^΄ } => x₁*x₂* …* x_φ(m) = x₁^΄ *x₂^΄ *…*x_φ(m)^΄.

Покажем, что (x₁*x₂* …* x_φ(m),m)=1.

МОП. Имеем, (x₁,m)=1 (x₂,m)=1… (x_φ(m) ,m)=1_.,т.к. x_i Пр.СВ_m => (x₁*x₂* …* x_φ(m),m)=1.

Пусть (x₁*x₂* …* x_φ(m),m)=d≠1>1 =>сущ-ет p- простой делитель d => dp => (x₁*x₂* …* x_φ(m) ) p и mp

=> В каждом из случаев получено противоречие с тем, что взаимно x_i и m взаимно просты, а из пр-ля мы получили, что (x_i ,m)=p .

Разделим обе части (**) на x₁*x₂* …* x_φ(m), которое взаимно просто с mod m => a^φ(m) ≡1(mod m).

След: (теорема Ферма)

а) Если p- простoе (p,a)=1 , то

a^p-1≡1(mod p)

Т.к. (p,a)=1 по т Эйлера по опр. ф-ии Э. => a^p-1≡1(mod p)

б) Если p-простое и aZ - произв., то

Срав-ия с одной переменной.

ОПР. Срав-ие вида (1), где не сравнимо с 0 по mod m наз. срав-ием степени n, x – символ, oбознач переменную.

Реш-м срав-ия (1) наз. класс , все эл-ты кот-го удовл-ют данному срав-ию.

Опр: Сравн-м 1-ой степени с 1 неизвест наз-ся срав-е вида ax≡b(mod m), где а≡0(mod m)

Два срав-ия равносильны, если совпадают мн-ва чисел, удов-ие каждому из них. Из опр. следует, что алгебр-е срав-ие вида ax≡b(mod m) назыв. срав-ием первой степени, если a не сравнимо с 0 по mod m.

Т: Если a и m - взаимно просты, то срав-ие ax≡b(mod m) имеет ед. решение.

Если НОД( a,m)=d>1и b не делится на d, то срав-ие ax≡b(mod m) не имеет решений.

Пр-р: 5х≡2(mod 6). (5,6)=1

x≡a5^φ(6)-1 φ(6)=φ(2)φ(3)=2. x≡2*5=10≡4(mod 6).