
М8 - 1.Векторы и операции над ними. Скалярное, векторное и смеш произведения векторов. Прилож к реш задач.
Отрезок,
для которого указано какая точка является
первой (начало), а какая второй (конец)
называется направленным
отрезком.
Обозначение:
![]() ,
,
![]() ,
,![]() .
.
Длинной
направленного
отрезка называется длина отрезка AB.
Обозначение:
![]() ,
,
![]() .
.
Направленный
отрезок называется нулевым,
если его начало совпадает с концом.
Обозначение:
![]() ,
,
![]() =0.
=0.
Направленные
отрезки называются коллинеарными,
если они лежат на одной прямой или
параллельных прямых. Обозначение:
![]() ||
||![]() .
.
Лучи АВ и CD называются сонаправленными, если они лежат на параллельных прямых и в одной полуплоскости с границей АС, в противном случае они называются противоположно направленными.
Направленные отрезки АВ и CD называются равными, если выполняются два условия:
1)эти
отрезки сонаправлены:
![]() ↑↑
↑↑
![]() .
2)длины отрезков равны:
.
2)длины отрезков равны:
![]() =
=
![]() .
.
Направленные
отрезки AB
иCD
называются сонаправленными,
если сонаправлены лучи AB
и CD.
В противном случае они называются
противоположно направленными. Обозн:
![]() ↓↑
↓↑
![]() .
.
Вектором плоскости называется множество всех равных между собой направленных отрезков.
Замечание1 Пользуясь аппаратом элементарной геометрии можно показать, что от данной точки можно отложить только один отрезок равный данному, поэтому вектор однозначно определяется любым своим направленным отрезком.
Замечание2 Опр коллинераности, сонаправленности и противоположности направленных векторов аналогичны соответствующим определениям для направленных отрезков.
Векторы называются компланарными, если они лежат на прямых, параллельных одной плоскости.
Векторы называются равными, если их множества полностью совпадают.
Сложение векторов
С
b![]() и
и
![]() называется такой вектор
называется такой вектор
![]() ,
который получается следующим образом:
,
который получается следующим образом:
![]() ,
,
![]() ,
,
![]() .
.
![]()
![]() A
B
A
B
a
c
О
Правила сложения векторов:
1.Правило треугольника:
m
n
![]()
2![]() .Правило
параллелограмма: (не для коллинеарных
векторов)
.Правило
параллелограмма: (не для коллинеарных
векторов)
![]() ;
;
![]() ;
;
![]() ;
;
![]() О А
О А
В
Умножение вектора на число
Произведением
действительного числа α на ненулевой
вектор
![]() называется такой в-р
называется такой в-р
![]() = α
= α
![]() ,
который удовлетворяет следующим
условиям:
,
который удовлетворяет следующим
условиям:
1.
![]() =|α|*
=|α|*![]() .
2. α=0,
.
2. α=0,
![]() =
=![]() α>0, то
α>0, то
![]() ↑↑
↑↑![]() α <0, то
α <0, то
![]() ↑↓
↑↓
![]() .
.
Скалярное произведение векторов
Скалярным
произведением векторов называется
число, равное произведению длин этих
векторов на cos
угла между ними:
![]() *
*![]() =(
=(![]()
![]() )=
)=![]() *
*![]() *cosα,
α=(
*cosα,
α=(![]() ^
^![]() ).
).
У![]() глом
между векторами
глом
между векторами
![]() и
и
![]() называется угол АОВ, полученный следующим
образом
называется угол АОВ, полученный следующим
образом
![]() ,
,
![]() А
А
О
В
Свойства скалярного произв-я:
1.Условие перпендикулярности векторов
Для того, чтобы два вектора были перп-ны, ↔ чтобы их скалярное произведение было равно 0.
Достаточность:
![]() *
*![]() =0.
Д-ть
=0.
Д-ть
![]() ┴
┴
![]() .
.
□![]() *
*![]() =
=![]() *
*![]() *cos
α =0 cosα=0
α=90
град.
*cos
α =0 cosα=0
α=90
град. ![]() ┴
┴
![]() .■
.■
Необходимость:
![]() ┴
┴
![]() .
Д-ть
.
Д-ть
![]() *
*![]() =0.
=0.
□![]() ┴
┴
![]() ,
когда cos
α=0
α=90
град
,
когда cos
α=0
α=90
град
![]()
![]() *
*![]() =
=![]() *
*![]() *0=0■
*0=0■
2.скалярный
квадрат вектора равен квадрату его
длины
![]() 2=
2=![]() 2.
2.
□![]() 2=
2=![]() *
*![]() =
=![]() *
*![]() *cos0
=
*cos0
=![]() *
*![]() =
=![]() 2.
■
2.
■
3.коммутативность
![]() *
*![]() =
=![]() *
*![]()
□![]() *
*![]() =
=![]() *
*![]() *cosα
=
*cosα
=
![]() *
*![]() *
cos
α
=
*
cos
α
=
![]() *
*![]() .■
.■
4.ассоциативность
скалярного произведения: (α![]() )*
)*![]() =
=![]() *(α
*(α![]() ).
).
Смешанное произвед-е векторов
Пусть
V
– ориентированное трехмерное
пространство. Смешанным
произведением
векторов
![]() (a1,a2,a3),
(a1,a2,a3),
![]() (b1,b2,b3),
(b1,b2,b3),
![]() (c1,c2,c3),
заданных своими координатами в некотором
ортонормированном базисе называется
число:
(c1,c2,c3),
заданных своими координатами в некотором
ортонормированном базисе называется
число:
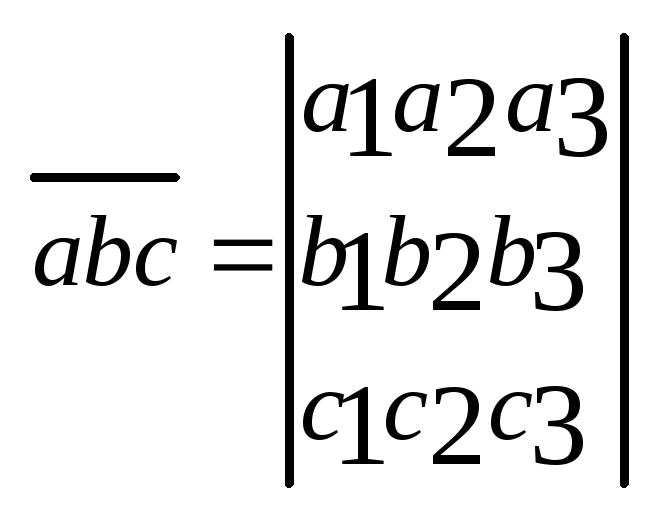 .
Это число не зависит от выбора базиса.
.
Это число не зависит от выбора базиса.
Св-ва смешанного произведения
1.
![]()
![]() ,
,
![]() ,
,![]() и любого
и любого
![]() справедливо
справедливо
![]()
![]()
![]() =-
=-![]()
![]()
![]() ,
,
![]()
![]()
![]() =-
=-![]()
![]()
![]() ,
,
![]()
![]()
![]() =-
=-![]()
![]()
![]() .
.
2.
![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]() .
.
3.
(![]()
![]() )
)![]()
![]() =
=![]() (
(![]()
![]()
![]() )=
)=![]() (
(![]()
![]() )
)![]() =
=![]()
![]() (
(![]()
![]() )=
)=![]()
![]()
![]()
![]() .
.
4.
(![]() )
)![]()
![]() =
=![]()
![]()
![]() +
+
![]()
![]()
![]() .
Аналогично для
.
Аналогично для![]() и
и
![]() .
.
Векторное произведение векторов
Векторным
произведением
векторов
![]() (a1,
a2,
a3),
(a1,
a2,
a3),
![]() (b1,
b2,b3),
заданных своими координатами в некотором
правом ортонормированном базисе
называется вектор
(b1,
b2,b3),
заданных своими координатами в некотором
правом ортонормированном базисе
называется вектор
![]() .
Обозначение
.
Обозначение
![]() х
х
![]() .
.
Св-ва векторного произведения
1.
![]() х
х![]() =-
=-![]() х
х![]() (антикоммутативность).
(антикоммутативность).
2. (![]()
![]() )
х
)
х
![]() =
=
![]() (
(![]() х
х
![]() )=
)=
![]() х(
х(![]()
![]() ).
).
3. (![]() х
х
![]() )
)![]() =
=
![]() х
х
![]() +
+
![]() х
х
![]() ,
,
![]() х (
х (![]() +
+![]() )
=
)
=
![]() х
х
![]() +
+
![]() х
х
![]() .
.
4.
![]() х
х
![]() =0.
=0.
Док-ва этих св-в вытекают из свойств определителя.
Пример задачи: дано

М8 - 2. Различные уравнения прямой и плоскости. Взаимное расположение прямых и плоск-ей. Прилож к реш задач.
Направляющим
вектором прямой называется любой
ненулевой вектор коллинеарный данной
прямой
![]() || L
,
|| L
,
![]() || L
,
|| L
,
![]() || L.
|| L.
![]() L
L
![]()
![]()
Теор
1: Каноническое
уравнение прямой имеет вид:
![]() ,
где М (x0;
y0)
,
где М (x0;
y0)![]() l,
l,
![]() ||
L.
||
L.
□ Выберем
репер R
(0; (![]() )).
Пусть М (x,y)
)).
Пусть М (x,y)
![]() l
(x,y)
– текущая точка l.
Если М
l
(x,y)
– текущая точка l.
Если М
![]() l,
то
l,
то
![]() ||
||![]() ,
,![]() =
=![]() (
(![]() ≠0)
≠0)
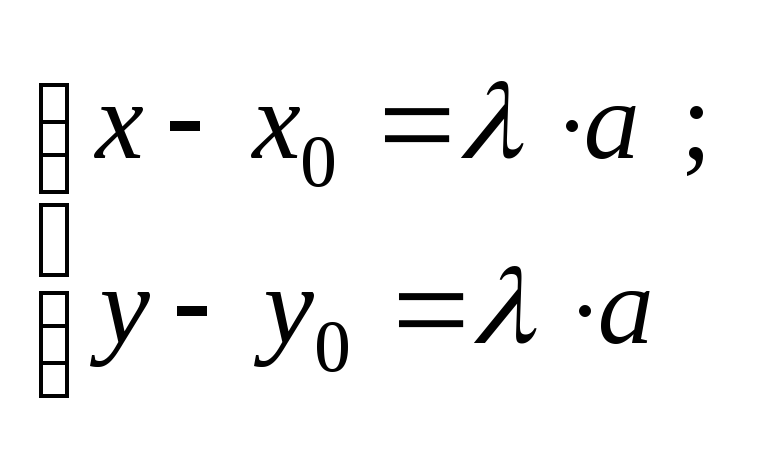 , откуда следует
, откуда следует
![]() ■
■
Замечание:
Если
a1
=0
, то прямая имеет уравнение
![]() x=x0
L
|| OY.
x=x0
L
|| OY.
Теорема2:
Уравнение
прямой проходящей через две точки имеет
вид:
![]() ,
где М1(x1;y1),
М2(x1
;y1)
,
где М1(x1;y1),
М2(x1
;y1)
![]() =
=
![]() .
.
Теорема3
Уравнение
прямой в отрезках на осях имеет вид:
![]() ,
А(а;0), В(0;b).
,
А(а;0), В(0;b).
Уравнение является частным случаем уравнения из Т2.
Теорема4:
Параметрическое
уравнение прямой имеет вид:
 ,
где М0(x0;y0),
M0
,
где М0(x0;y0),
M0![]() L
L
![]() (а1;а2),
(а1;а2),
![]() || l
,
|| l
,
![]() - любой действительный параметр.
- любой действительный параметр.
□ Пусть
R
– ортонормированный репер. М(x;y)
![]() L.
L.
![]() ||L;
||L;
![]() ||
||
![]() ;
;
![]() =
=![]() ;
;
 ;
;
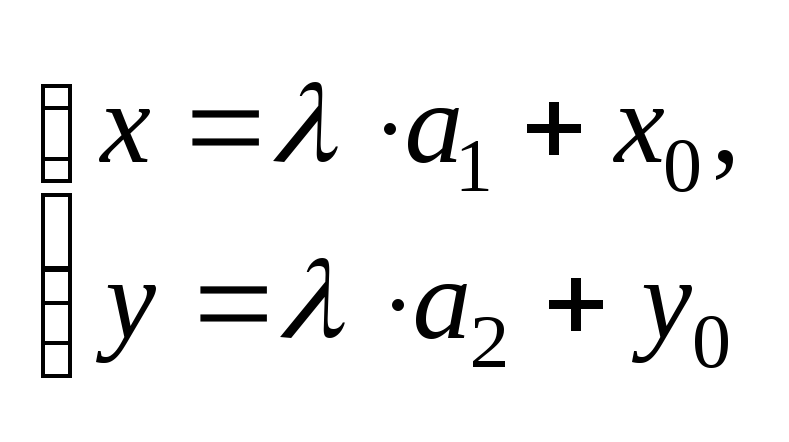 ■.
■.
Теорема
5: Уравнение
прямой с угловым коэффициентом имеет
вид:
![]() .
.
□ Пусть
R-ортонормированный
репер М(x;y)![]() L
L
![]() ||
L.
||
L.
![]() ,
k-ордината
направляющего вектора.
,
k-ордината
направляющего вектора.
![]() ;
;
![]() y=kx+b
■.
y=kx+b
■.
Прямая в пространстве
Прямая
задана точкой М (x0,
y0,
z0)
вектором
![]() в некоторой АСК. L={M/
в некоторой АСК. L={M/![]() ||
||![]() }.
М (x0,
y0,
z0)
}.
М (x0,
y0,
z0)
![]() L,
то (x-x0,
y-y0,
z-z0)
||
L,
то (x-x0,
y-y0,
z-z0)
||![]() (p1,p2,
p3).(*)
(p1,p2,
p3).(*)
![]() M0M
|| t
M0M
|| t![]() .
.
 -
параметрическое уравнение
прямой.
-
параметрическое уравнение
прямой.
Условие
(*) может означать также следующее:
![]() -каноническое
уравнение прямой;
-каноническое
уравнение прямой;
![]() - уравнение
прямой по двум точкам.
- уравнение
прямой по двум точкам.
Аналитическое задание плоскости.
Пусть
плоскость
![]() задана в АСК точкой М0
(x0,
y0,
z0)
и компланарными ей векторами
задана в АСК точкой М0
(x0,
y0,
z0)
и компланарными ей векторами
![]() (a1,a2,a3),
(a1,a2,a3),
![]() (b1,b2,b3),
(b1,b2,b3),
![]() ⌐||
⌐||
![]() .
.
![]() ={М/
={М/![]() ,
,
![]() ,
,
![]() - компланарны}
- компланарны}
М
(x,y,z)![]()
![]()
![]()
![]() =0
(смешанное произведение, условие
компланарности трех векторов)
=0
(смешанное произведение, условие
компланарности трех векторов)
![]()
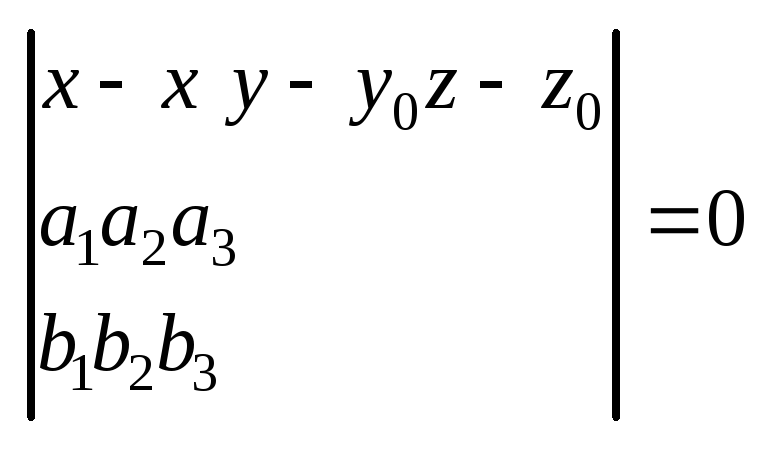 .
(1)
.
(1)
Всякая плоскость задается в АСК уравнением 1-й степени Ax+By+Cz+D=0 (2), A,B,C <> 0 одновременно и наоборот, всякое уравнение 1-й степени (2) есть уравнение полскости.
Взаимное расположение прямой и плоскости.
Пусть
в АСК
![]() :
Ax+By+Cz+d=0;
l:
M0
(x0,y0,z0),
:
Ax+By+Cz+d=0;
l:
M0
(x0,y0,z0),
![]() .
.
Возможны следующие случаи расположения прямой и плоскости:
1)
![]()
p
⌐||
p
⌐||
![]()
Ap1+Bp2+Cp3
<>0
2)
Ap1+Bp2+Cp3
<>0
2)
![]() p
||
p
||
![]() ,
М0
,
М0
![]()
![]()
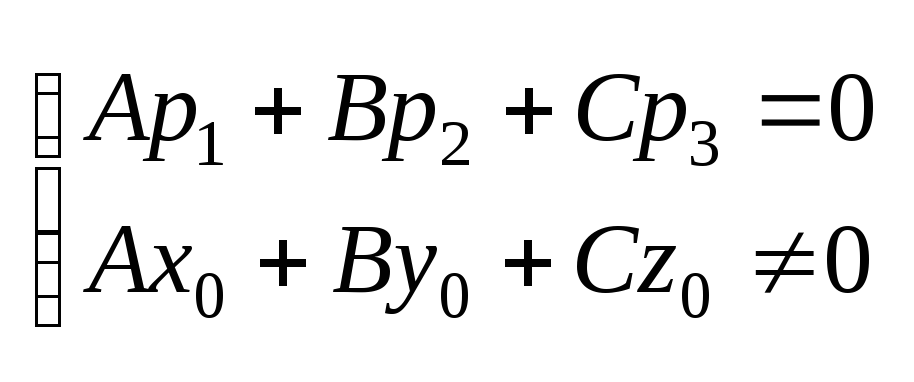
3 )
)
![]()
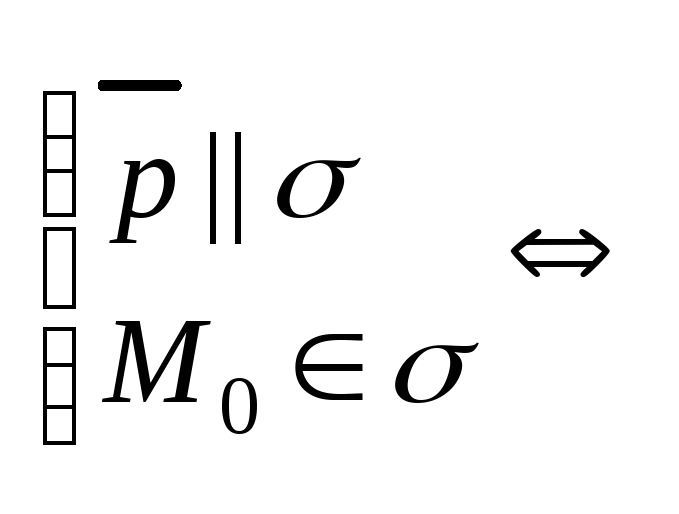
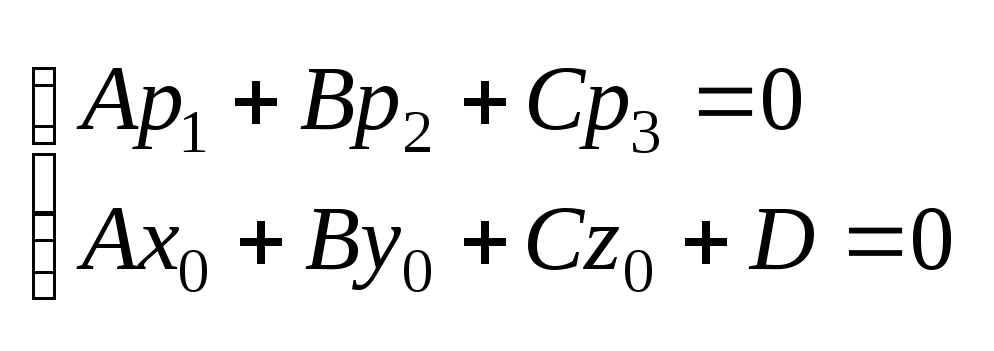
Задача: дано прямые
l1:
![]()
l2:
![]()
Выяснить их взаимное расположение.
Решение:
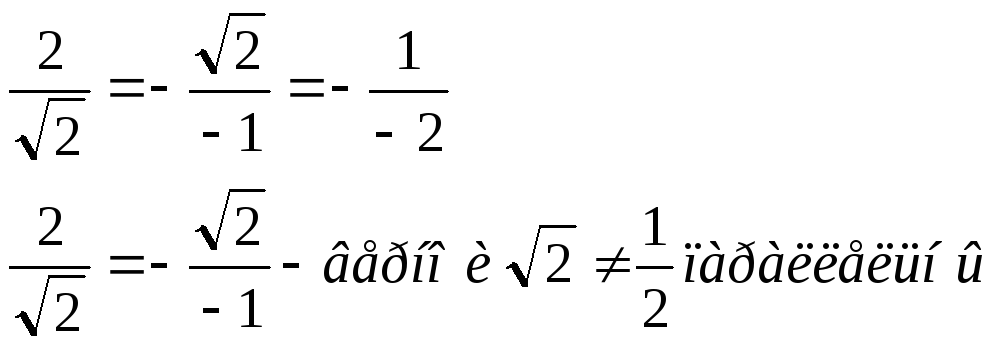
М8 - 3.Линии и поверхности второго порядка. Классификация.
Эллипсом
называется
множество точек плоскости, сумма
расстояний которых до двух данных точек,
называемых фокусами, есть величина
постоянная, большая, чем расстояние
между фокусами.
![]() ,
,
![]()
a=KO, с=F2O.
Теорема1.
Если
точка M(x;y)
принадлежит эллипсу, то ее координаты
удовлетворяют уравнению:
![]() (1).
– каноническое уравнение эллипса.
(1).
– каноническое уравнение эллипса.
Теорема2.
Если
Координаты
т. М удовлетворяют уравнению (1), то она
принадлежит эллипсу
![]()
Свойства эллипса
1.Эллипс не проходит ч/з начало координат
Т.к. коорд нуля не удовлетворяют уравнению эллипса, значит он не проходит ч/з начало координат.
2.Эллипс симметричен относит оси Ох
□ М
(х;у)
![]() эллипсу; М1
(х;-y).
эллипсу; М1
(х;-y).
![]() M1
M1![]() эллипсу.■.
эллипсу.■.
3.Эллипс симметричен относит оси Oy.
□ М
(х;у)
![]() эллипсу; М2
(-х;y).
эллипсу; М2
(-х;y).
![]() M2
M2![]() эллипсу.■.
эллипсу.■.
4.Эллипс симметричен относительно начала координат.
□ М
(х;у)
![]() эллипсу;
М3
(-х;-y).
эллипсу;
М3
(-х;-y).
![]() M3
M3![]() эллипсу.■.
эллипсу.■.
5.Точки
пересечения эллипса с осями координат:
Ох: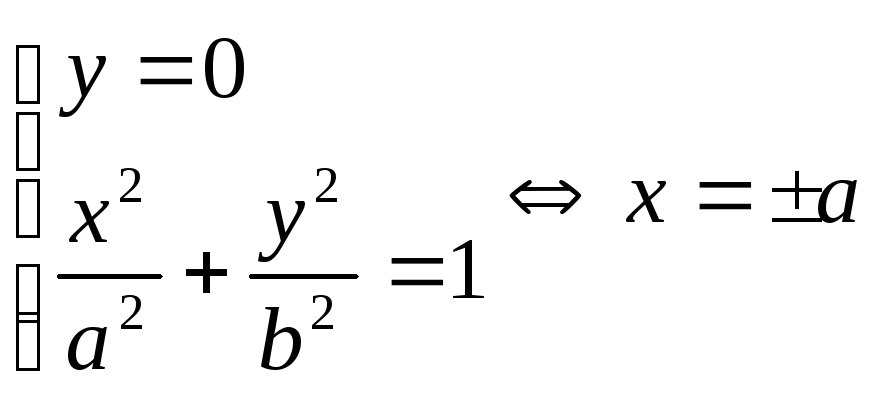 A1(a;0),
A2(-a;0).
Oy:
A1(a;0),
A2(-a;0).
Oy:![]() B1(0;b),
B2(0;-b).
B1(0;b),
B2(0;-b).
6.
![]() .
Область определения этой функции
.
Область определения этой функции
![]() или –a<=x<=a.
Область значений
или –a<=x<=a.
Область значений
![]() или –b<=y<=b.
или –b<=y<=b.
Параметрические
уравнения эллипса можно записать в
таком виде:

Дерикториальное св-во эллипса.
Пусть
дано уравнение эллипса, на котором дана
точка М0(x0;y0).
Фокальные радиусы т. М определяются
следующими формулами:
![]() ,
,
![]() (2).
(2).
Отношение
фокального расстояния эллипса к его
большей оси называется эксцентриситетом
эллипса:
![]() .
Формулы (2) можно записать в следующем
виде:
.
Формулы (2) можно записать в следующем
виде:
![]() ,
,
![]() ,
причем
,
причем
![]() ,
так как 0<=c<a.
Для окружности, являющейся частным
случаем эллипса
,
так как 0<=c<a.
Для окружности, являющейся частным
случаем эллипса
![]() =0.
=0.
Директрисами
эллипса называются прямые, параллельные
малой оси эллипса и удаленной от нее на
расстояние
![]() .
Обозначение: d1,
d2.
.
Обозначение: d1,
d2.
Для
любой точки эллипса отношение ее
фокального радиуса к расстоянию до
соответствующей директрисы есть величина
постоянная, равная эксцентриситету,
т.е.
![]() .
.
Гиперболой называется множество точек плоскости, для которых абсолютное значение разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстояний между фокусами.
F1F2=2c
– расстояние между фокусами F1
и F2.
Тогда для любой точки гиперболы
![]() ,
a<c.
Так как F1M=
,
a<c.
Так как F1M=![]() ,
F2M=
,
F2M=![]() ,
то можем записать |
,
то можем записать |![]() -
-![]() |=2a,
откуда
|=2a,
откуда
![]() (1) – каноническое уравнение гиперболы.
(1) – каноническое уравнение гиперболы.
Теорема: Если координаты т. М (x;y) удовлетворяют уравнению (1), то эта точка принадлежит гиперболе.
Свойства гиперболы
1.Гипербола не проходит через начало координат.
□
![]() 0-0=1. Так как координаты
нуля не удовлетворяют условию гиперболы,
то она не проходит через начало координат.■
0-0=1. Так как координаты
нуля не удовлетворяют условию гиперболы,
то она не проходит через начало координат.■
2.Гипербола симметрична относительно оси Ох, оси Оy и начала координат.
□ М(x;y),
M1(x;-y).
![]()
![]() ■.
■.
3.Точки
пересечения гиперболы с осями координат:Ox:
 A1(a;0),
A2(-a;0)-
вершина гиперболы. сOy:
A1(a;0),
A2(-a;0)-
вершина гиперболы. сOy:

![]() .-
гипербола не пересекает ось Оy.
С прямыми:
y=kx:
.-
гипербола не пересекает ось Оy.
С прямыми:
y=kx:
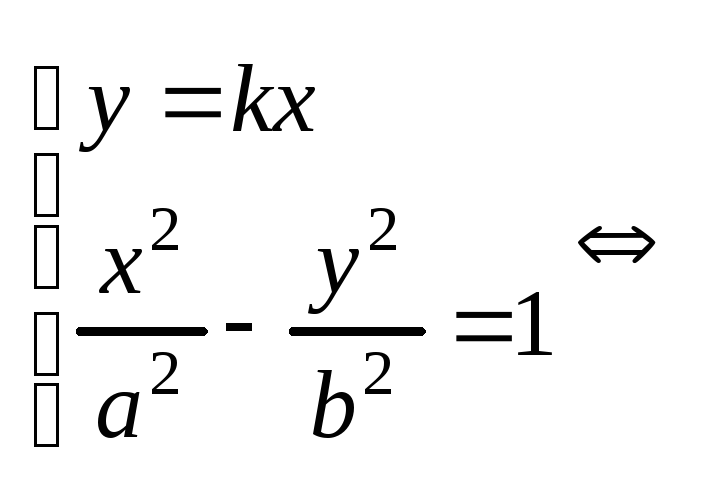
![]()
![]() .
.
4.Неограниченность
гиперболы:
![]() ;
;
![]() ;
;![]() ;
;![]()
![]() .
.
5.Прямые
![]() являются асимптотами гиперболы.
являются асимптотами гиперболы.
Эксцентриситетом
гиперболы
называется число, которое обозначается
![]() .
.
0<=
![]() <=1
(для эллипса); a2+b2=c2
<=1
(для эллипса); a2+b2=c2
![]() ;
;
![]() ;
;
![]()
![]() (для гиперболы).
(для гиперболы).
После
уменьшения гиперболы уменьшается ее
эксцентриситет, и она сильнее сжимается
к оси Оx.
F1M=![]() ;
F2M=
;
F2M=![]() - фокальные радиусы гиперболы.
- фокальные радиусы гиперболы.
Гипербола
имеет две директрисы, ими являются
прямые с уравнениями
![]() .
.
Касательная
к гиперболе задается таким уравнением
![]() ,
где (x0;y0)
– точка касания.
,
где (x0;y0)
– точка касания.
Равносторонняя
гипербола задается уравнением:
![]()
![]() x2-y2=a2.
x2-y2=a2.
Параболой называется множество точек плоскости, равноудаленных от одной точки, называемой фокусом и данной прямой, не проходящей через фокус, которая называется директрисой.
Р![]() асстояние
между фокусом и директрисой всегда
равно FD=p
и называется фокальным диаметром.
асстояние
между фокусом и директрисой всегда
равно FD=p
и называется фокальным диаметром.
Теор1:
Если
точка М(x;y)
принадлежит параболе, то в канонической
системе координат ее уравнение имеет
вид
![]() (1).-
каноническое уравнение параболы.
(1).-
каноническое уравнение параболы.
□ F(p\2,0), x+p\2=0 – уравнение директрисы.
МF=MD1 D1(-p\2;y)
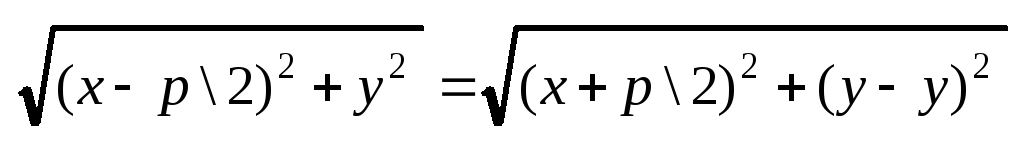 x2-px+p2\4+y2=x2+px+p2\4
x2-px+p2\4+y2=x2+px+p2\4
![]()
![]() ■.
■.
Теорема2: Если координаты т. М удовлетворяют уравнению (1), то точка M принадлежит параболе.
□ MF=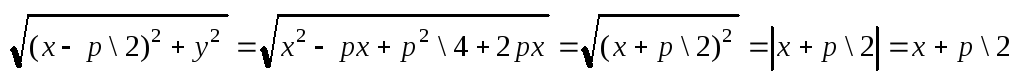 ;MD1=
;MD1= ;
MF=MD,
М принадлежит параболе. ■.
;
MF=MD,
М принадлежит параболе. ■.
Свойства параболы.
1.Область
определения параболы – 1-я и 4-я четверти:
x>=0,
![]() .
.
2.Парабола проходит через начало канонической системы координат: x=0 y2=2px y=0, 0(0;0)-вершина параболы.
3.Парабола симметрична только относительно оси Оx.
M (x;-y); y2=2px; (-y)2=2px y2=2px. Несимметрична относительно Oy. M(-x;y) y2=-2px – не верно.
4.
Эксцентриситет параболы:
![]() .
.
![]()
Уравнение
касательной к параболе имеет вид
![]() ,
(x0;y0)
– точка касания.
,
(x0;y0)
– точка касания.
Классификация кривых второго порядка:
Уравнение кривой второго порядка изменяется при переходе к другой системе координат.
Теорема1: существует 9 и только 9 кривых второго порядка:
1.эллипс:
![]() .
.
2.гипербола:
![]() .
.
3.парабола:
![]() .
.
4.пара
действительных пересекающихся прямых:
![]() .
.
5.пара
мнимых пересекающихся прямых:
![]() .
.
пара действительных параллельных прямых: x2-a2=0.
6.пара мнимых параллельных прямых: x2+a2=0
7.пара совпадающих прямых: x2=0.
8. мнимый
эллипс:
![]() .
.
Теорема2:
Если
кривая второго порядка в некоторой
прямоугольной системе координат имеет
уравнение:
![]() ,
где a11,
a12,
a22
– одновременно не равны нулю, то всегда
существует прямоугольная система
координат, в которой a12=0.
,
где a11,
a12,
a22
– одновременно не равны нулю, то всегда
существует прямоугольная система
координат, в которой a12=0.
Теорема3:
Если
уравнение кривой второго порядка имеет
вид:
![]() ,
то всегда существует другой ортогональный
репер, в котором это уравнение имеет
вид:
,
то всегда существует другой ортогональный
репер, в котором это уравнение имеет
вид:
1.Ax2+By2+C=0, A<>0, B<>0. В этом случае a11<>0, a22<>0.
![]() ,
,
 .
.
2.Ax2+By+C=0, A<>0,B<>0. В этом случае a23<>0, a22=0 или a11=0, a13<>0.
![]() ,
,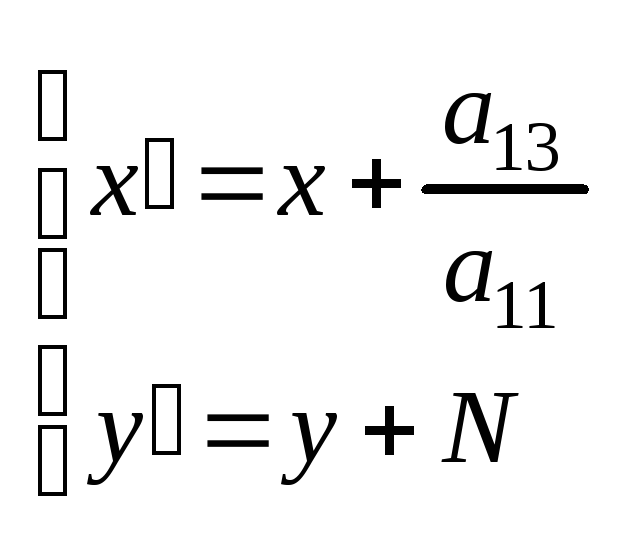 .
.
3.Ax2+B=0, A<>0. В этом случае a22=0, a23=0 или a11=0, a13=0.
![]() ,
,
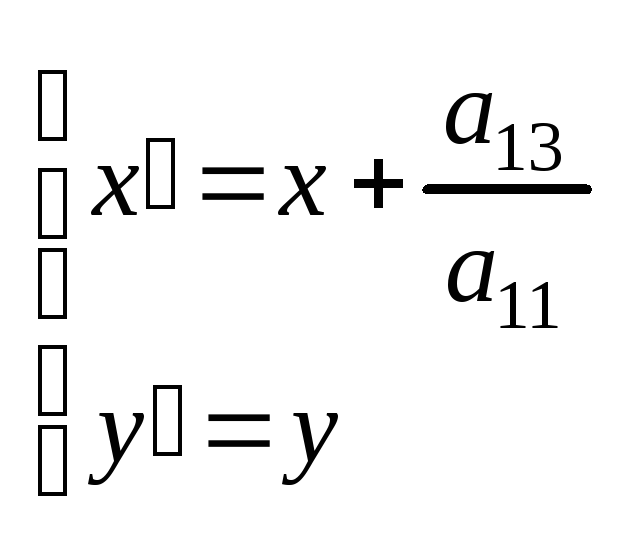 .
.
Задача: выяснить какая линия задана уравнением 4x2-y2+16x-6y+3=0. Записать в каноническом виде.
(4x2+16x+16)-16-( y2+6y+9)+9+4=0
(2x+4)2-(y+3)2=4
4(x+2)2-(y+3)2=4
(x+2)2/1-(y+3)2/4=1 – гипербола с центром M0(-2;-3)
М8 - 4. Преобразования плоскости. приложения к решению задач.
Опр. Говорят, что дано отображение f (функция) множества X в множество Y, если каждому элементу х множества X поставлен в соответствие определенный элемент у множества У .
Обозначение, f : X -> У - отображение f множества X в множество Y.
X - область определения, f(X) - область значений; у = f(x) - образ элемента х € X; х - прообраз элемента у € V.
Опр. Отображение f : X -> К называется инъективным если каждым двум различным элементам множества X соответствуют два различных элемента множества Y; .
сюрьективным, если f(X) = У, т. е. каждый элемент множества Y является образом по крайней мере одного элемента множества X;
взаимно- однозначным или биективным, если оно является одновременно сюръективным и инъективным.
Опр. Преобразованием фигуры Ф называется любое биективное отображение фигуры Ф на себя.
Теорема (о группе преобразований). Множество G всех преобразований фигуры Ф есть группа.
Опр. Подгруппой Н группы G называется подмножество II группы G, являющееся группой относительно бинарной операции, определенной в G.
Теорема (о подгруппе). Для того, чтобы подмножество Н группы G было подгруппой, необходимо и достаточно, чтобы выполнялись два условия; 1°. Если f € H, g € H, то g0f € H . 2°. Если f €H, то f-1 €H.
Движение плоскости
![]()
Опр. Пусть имеются две прямоугольные декартовы системы координат Oij (i,j i`,j`- векторы) и O'i'j', при этом |i|=|j|=|i'|=|j'|=1. Тогда преобразование плоскости, которое каждой точке М с координатами (x, у) относительно Oij ставит в соответствие точку М' с теми же координатами (х,у), но относительно O'i'j', называется движением плоскости.
Из определения следует, что тождественное преобразование плоскости является движением.
Основное свойство движения. Движение плоскости сохраняет расстояние между любыми двумя точками плоскости, т. е. для любых точек М, N и их образов М', N' выполняется равенство |M'N'| = |MN|.
Доказательство. Пусть М(х1,у1) и N(x2,y2) относительно Oij. Тогда |MN| = √((х2-x1)2 + (y2 – y1)2) - Образы М', N'.точек М, N имеют соответственно те же координаты (x1.y1), (x2,y2) относительно системы координат О` i' j' и поэтому |M'N'| = √((х2-x1)2 + (y2 – y1)2) = |MN|.
Свойства движения.
1° Движение плоскости всякую прямую отображает в прямую.
Доказательство, Пусть f - движение, заданное с помощью систем координат Oij и 0'i`j', и £ - некоторая прямая, определяемая уравнением Ах + Ву + С = 0 (1)относительно системы координат Oij. Пусть точка. М €£ , тогда ее координаты удовлетворяют уравнению (1). Точка. М' = f(М) имеет те же координаты, что и точка М, и поэтому множество f(L) образов всех точек М € L определяется в системе координат О'i' j' тем же уравнением (1), а потому является прямой £'.
2°. Движение плоскости отображает полуплоскость с границей £ в полуплоскость с границей £', где L` = f(£),
Опр. Простым, отношением трех точек А, В, С, лежащих на одной прямой (коллинеарных) и взятых в указанном порядке, называется отношение коллинеарных векторов АО и ВС.
Обозначение.
(АВ,С) — простое отношение точек А, В. С.
По определению

3°. Движение плоскости сохраняет простое отношение трех точек прямой.
Опр. Будем говорить, что точка С лежит между точками А и В, если точки А, В. С лежат на одной прямой и точка. С делит отрезок АВ в отношении λ > 0.
4°. Движение плоскости сохраняет отношение "лежать между".
5°. Движение плоскости отображает отрезок в равный ему отрезок, луч в луч.
6°. Движение плоскости отображает угол в равный ему угол.
7°. Движение плоскости отображает параллельные прямые в параллельные прямые.
Опр.
Пусть f
- преобразование плоскости. Вектор a'
называется образом вектора а, если
вектор а' = вектор А'В', где А' =f(А),
В` = f(В),
![]() .
Заметим, что образ а' не зависит от выбора
представителя вектора АВ вектора а, что
следует из свойства 2) и следствия к
нему.
.
Заметим, что образ а' не зависит от выбора
представителя вектора АВ вектора а, что
следует из свойства 2) и следствия к
нему.
8°. Движение плоскости отображает вектор в вектор, сумму векторов в сумму векторов и произведение числа на вектор в произведение того же числа на соответствующий вектор.
Теорема Если движение f задано двумя системами координат Oij и O'i'j'. при этом угол i,i' = φ и О'(х0,у0)Oij , то координаты любой точки М(х,у)Oij ее образа М'(х',у')Oij связаны соотношениями: х` = х cos φ – εу sin φ + х0,
у' = х sin φ + εу cos φ + х0 (1.2.5) где ε = ±1.
Теорема (обратная). Пусть Oij — некоторая прямоугольная декартова система координат. Если преобразование f плоскости каждой точке М(х,у) ставит в соответствие точку М'(х',у'), при этом имеют место равенства (1.2.5), то f является движением.
Теорема. Движение плоскости вполне определяется формулами (1.2.5),
Заметим, что при ε = +1 системы координат Oij и O'i!j' одинаково ориентированы, а при ε = - 1 противоположно ориентированы.
Опр. Движение плоскости, определяемое формулами (1.2.5), называется движением первого рода, при ε= +1 и движением второго рода при ε = - 1.
Опр. Осевой симметрией плоскости с осью симметрии L называется преобразование плоскости, которое всякой точке М ставит в соответствие точку М' по закону: 1) ММ' перпендик L
2) КМ = КМ', где К = ММ' пересек L. Обозначение. SL - осевая симметрия с осью симметрии L.
