ГОС / MODUL_5_DIF_URY

М5 - 1 Обыкновенные диф. ур-ния. Основные понятия. Диф. Ур-ния 1 порядка.

Опр. Обык.диф.ур-ем n-го порядка назыв.ур-е вида где F – известная ф-ция своих аргументов,зад. в нек.области, x-незав.переменная, y-ф-я перемен.х,

Опр.Порядком ОДУ(1) назыв.порядок наивысшей производной неизв.ф-ии y, входящей в дан.ур-е.

Опр. Решением диф. ур-ия (1) на пром-ке I наз-ся ф-ция y=φ(x), имеющая на пром-ке I все производные до n-го порядка включ-но, такая, что , .

Опр. График реш-я диф. ур-ния наз-ся интегральной кривой этого ур-ия.

Опр. Диф. ур-ие, разрешенное относ-но производной наз-ся ДУ 1-го порядка и имеет вид:

Пример:

Уравнения 1пор-ка резреш.относит-но произв.имеют вид:

Опр.пред, что п.ч.ур-я опред. в некот.области.Ф-я наз.решениемв(a,b),

е/и:1)сущ. для всех х из (a,b)

2)ф-яобращ.ур-ев верное рав-во справедл. для всех х из (a,b)

Геом.смысл.решения.Поле направлений.

Б.рассм.х и у как декартовы корд.на плоскости=> реш-юур-я б.соотв.некот.кривая данного ур-я,кот.наз-ся интегр.кривой.. Рассм. ур-е ,где а опред.в некот.области G.Это ур-е задает в каждой (.)(х,y)из G знач-е угл.коэф.касат, проход.ч/з эту (.)интегр.кривой.Е/и в каждой (.)(х,y)из G с помощью нек.отрезка предст.направ-е касат,опред.знач-ем f(x.,y), то получ. поле напр-ий.

Задача Коши: среди всех решений ур-я найти такое решение ,при кот.ф-яприним.задан.числовое зн-е y₀ при заданном x₀ .Геом-и з.Коши можно сформ.так: среди всех инт.кривых ур-янайти ту, кот.прох ч/з зад.(.) (x₀ y₀ )

Опр. Общим решением ДУ в области G наз.ф-я ,завис.от произв.const c и удовл.условиям:1) явл.реш-ем ур-япри люб.конкр.значении с из нек.множ-ва.2)для люб. (.) (x₀ y₀ ), леж.внутри G,сущ.такое с=с₀ , что ф-я удов.нач.усл.

Опр. Реш-е, содержащееся в общем реш-и , т.е. полученное из ф-лыпри конкретном допустимом числовом знач-и с наз-ся частным реш-ем ДУ.

Опр. Процесс отыскания общ.ре-я ДУ приводит к ур-ю Φ(x,y,c)=0, кот.наз-ют общим интегралом ДУ.

Опр. Ур-е вида ,Л.Ч.ккоторого есть полный диф-ал нек.ф-ии наз-ся ур-ем в полных диф-ах.

Опр. Ур-ие вида .гдеопредлены и непрер.в интервалах наз. ур-ем с разделяющимися переменными.

Общее реш-е ДУ(1) имеет вид

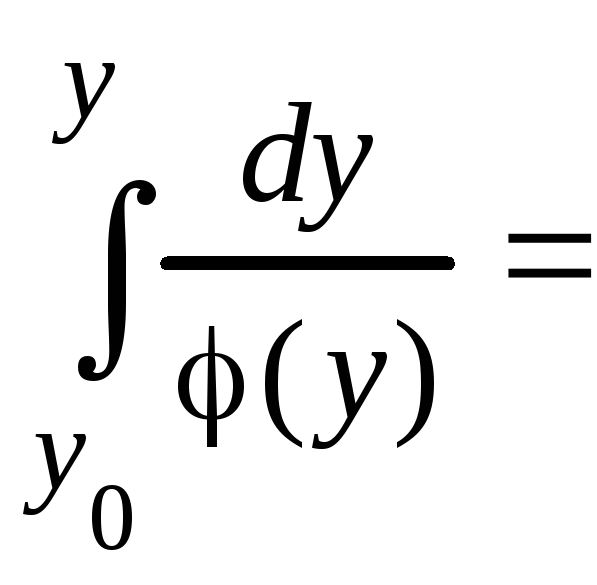
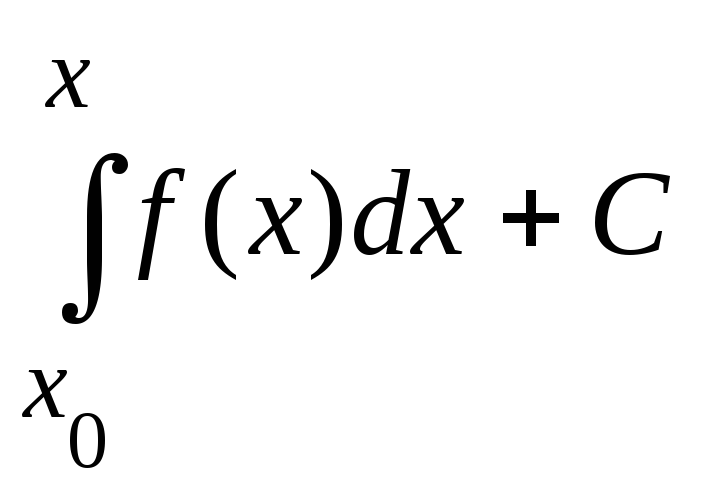
Опр. Ур-ие вида (4) наз-ся ЛДУ 1го порядка (ф-ции p(x), g(x) непрерывны на (a,b)). Если на (a,b), то ур-ие (1) наз-ют НЛДУ 1го порядка. Если на (a,b), то ур-ие (1) наз-ют ОЛДУ 1го порядка, соответствующим данному неоднородному.

Решение ОЛДУ: общий интеграл имеет вид:

,а общее реш-е:

y=0(кот.потеряно при делении на y явл.особым реш-ем ур-я

Решение НЛДУ методом вариации произв.постоянных.

1)запис. ОЛДУ,соотв.данному неднор-му:

2)Запис.реш-е

3)общее решение НЛДУ ищется в виде ф-ии

4)Подставляя эту ф-ю в ур-е(1), получаем Интегрируя (4)найдем

Итак, общее реш-е НЛДУ имеет вид:

Т: общее решение НЛДУесть сумма общего решения соответсв. ОЛДУ и частного реш-я НЛДУ.

М5-2 Лин-е ДУ 2го порядка с пост-ми коэф-ми. Их прилож-я.

Опр. Ур-ие вида (1), где , ф-ция f(x) непрерывна на (a,b) наз-ся НЛДУ 2го порядка с пост-ми коэф-тами.(ПК)

Опр. Ур-ие вида (2) наз-ют ОЛДУ 2го порядка с ПК, соотв-щим данному неоднор-му.

Свойства решений ОЛДУ 2го порядка

Т 1.если является реш-ем ОЛДУ, то и , где с-произв. Const, также явл.реш-ем ОЛДУ

Т2. Если и -решения ОЛДУ, то и их сумма также является решением этого уравнения.

Следствие:Если и -решения ОЛДУ, то ф-я -также реш-е этого ур-я

Опр.2 ф-ии и наз.л/зав на нек. промежутке, е/и можно подобрать такие числа и не равные нулю одновременно, что лин. комбинация этих ф-ий тождественно равна нулю на этом промежутке, т. е.

Если таких чисел подобрать нельзя,то функции наз. л/ нез.на указ.промежутке.

Ф-иии будут л/зав. тогда и только тогда, когда их отношение постоянно, т. е.

Опр.М-во реш-ий ОЛДУ, опред. и л/ нез.на (а,b)наз-ся ФСР этого ур-я на (а,b)

ОЛДУ 2 порядка пост. коэф-ми

,его харакатеристическим явл.

Т. Пусть дано ОЛДУ 2го порядка с ПК (2) и λ₁, λ₂ - корни хар-го ур-ия λ²+ λp+q=0.

1). λ₁, λ₂ – корни действит и различны, сис-ма реш имеет вид:

Эти решения л/н, т.к. их отношение

След-но реш-я образ.ФСРТогда общ.реш-е иммет вид:

Пример:

Тогда

ФС Р:

Общее реш-е:

2) Корни комплексно-сопряженные. λ₁=a+bi, λ₂=a-bi, b<>0. По предыдущему, , -решения и они л/н. Рассмотрим

Они яв-ся решениями Ур-ия как лин комбинация реш-й. Они л/н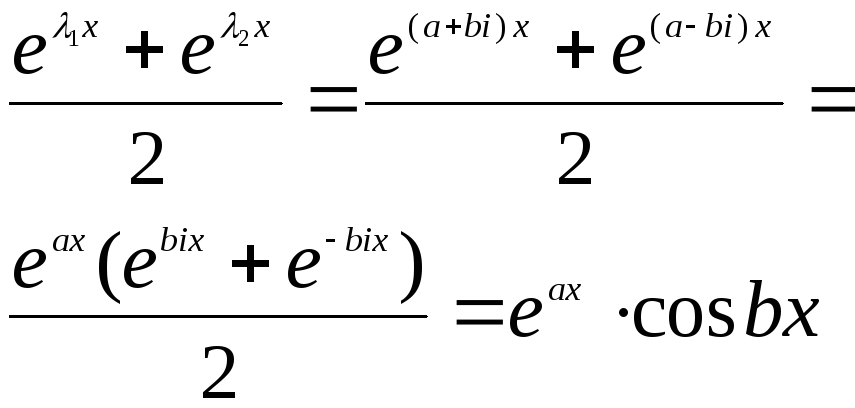

(по ф-ле Мувра).

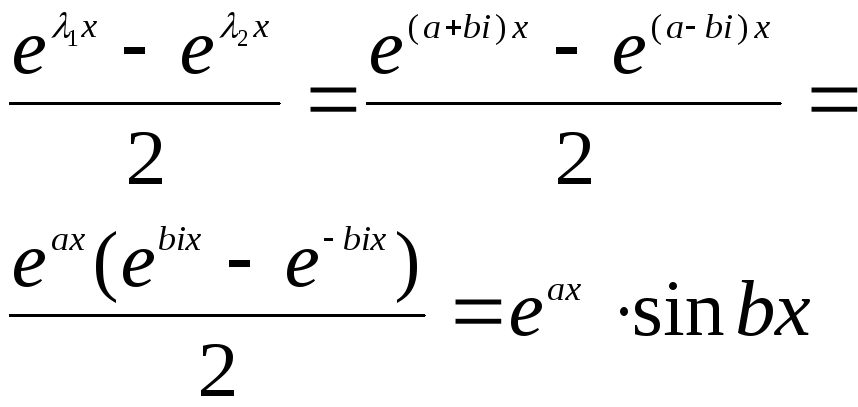
Значит ФСР

Общее реш-е:

3) Корни урав-я λ²+ λp+q=0 равны

(λ₁=λ₂ )

Тогда

Преобр-ем Л.Ч.характ.ур-я

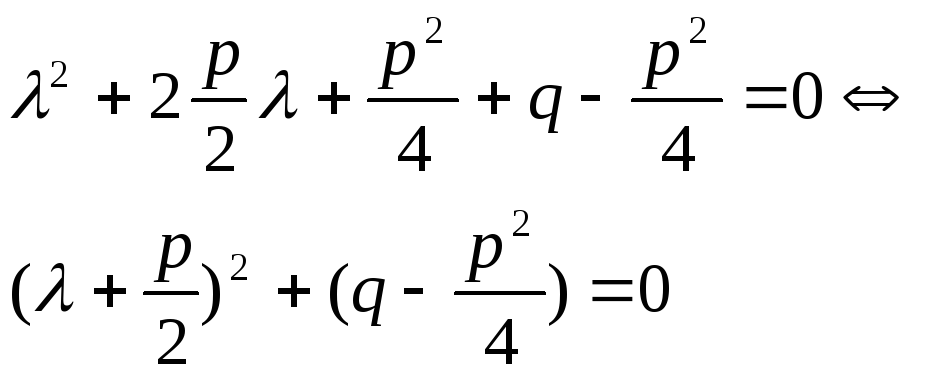
В силу (*):

Однако, частным реш-ем ур-я (2) явл..Убедимся, что -это 2ое реш-е ур-я(2)

Подставимв ур-е(2)

С учётомполуч:

Общ.реш-е:

Общее решение НЛДУ 2го порядка с ПК.

(1), где , ф-ция f(x) непрерывна на (a,b).

1). Правая часть ур-ия(1) имеет вид -или q(x)=P_m(x)sinαx+Q_m(x)cosαx и α не яв-ся корнем характер-го Ур-ния, тогда частное реш-е: q(x)=D_m(x)e ^αx и q(x)=A_m(x)sin αx+B_m(x)cos αx,

P_m(x), Q_m(x), A_m(x), B_m(x),D_m(x) – многочлены степени m.

2). Правая часть ур-ия(1) имеет вид -или q(x)=P_m(x)sinαx+Q_m(x)cosαx и α яв-ся корнем характер-го ур-ния кратности k, 1<=k<=2, тогда частное реш-е: q(x)=x^k D_m(x) и q(x)= x^k(A_m(x)sin αx+B_m(x)cos αx)

3).Общее реш-е неоднор-го Ур-ия получаем в виде суммы ощего реш-я однор-го и частного реш-я неоднор-го.

Метод вариации произв.пост. (метод Лагранжа)

метод раб,е/и известна ФСр лин.у-я.

Пусть -ФСр соотв. однор.ур-я

Ищем общ.реш-е(*)в виде , полагая, что -ф-ии, завис.от х.Нужно их найти.

Находим и

В конечном итоге получ.систему:

Интегрируя произв. получ. .Общ.реш: