М6,7 - 1.Поле комплексных чисел.

Отсутствие в R решения уравн x²=-1вынуждает найти такую числ систему, в кот оно бы имело реш.Этого можно добиться, добавив вR элемент i, т.ч. i²=-1 Обозн C.

Опр.Выражение a+bi, где a,b –действ.числа, i-мнимая единица называется к.ч.(a-действ.часть,b-мнимая часть)

Опр.2 к.ч.равны, если равны их дейст. И мнимые части.

Операции…

Т: <C;+,*> -поле

Док-во:

0. С-замнкуто относительно + и *

1.Абелева гр по +

a)КММ+ b)ACC+ в)нейтр эл по + 0 г)наличие против. к.ч.

2. Абелева гр по *

a)КММ*б)АСС*в)нейтр эл по * 1+0i г)обратимость люб.ненул.к.ч.

3.Нейтр.эл по * отличен от н.э. по +

Док-во КММ+: пусть z₁ =a+bi и z₂=с+di

z₁ + z₂ = (a+bi)+(c+di)=(a+c)+(b+d)i=(c+a)+(d+b)i

(т.к.на R слож-е КММ)

Док-во наличие н.э.по*

=1+0i из С. Пусть z =a+bi. z=(1+0i)(a+bi)=a+bi=z

Т: поле <C;+;*>– явл алгебраич расширением поля <R;+;*>.

Опр. 2 к.ч. являются сопряж, если имеют один. Действ. Части и против. мнимые.(2+7i и 2-7i) св-ва

Формы предст.к.ч

1) алгебр.форма z =a+bi

2)геом.форма(точка с корд(a,b) на дек пл-ти) Рис

3) показат-я форма записи.

Опр. Модулем к.ч.называется длина радиус-вектора.

Опр. Арг.к.ч. наз.угол между полож.напр.оси ОХ и лучом oz, отсчитыв. Против час стрелки .(Arg (z)= (опред. С точн. 2пи)

-триг.форма записи к.ч.

Прим z=1-i

|z|=корень из 2 =-Пи/4

3) cosф+isinф=e^iф, z=|z|*e^iф.

СВ1,2: пусть z₁ , z₂ из С

докВ силу единств тригоном формы записи

СВ3,4:

Формула Муавра:пусть z=|z|(cosφ+isinφ), тогда

zⁿ=|z|ⁿ(cos nφ +isin nφ) (частн. Случ.)

Доказ индукцией по степени

1.Базис.n=1

n=2

2.инд.щаг. Предп. Что утв.верно при n=k

Докажем, что z^k+1 вычислеятся по фле

Опр. Корнем n-степени наз.к.ч. n-ая степень которго равна z.

Т: извлечение корня n-степени из числа Z≠0 всегда возможно и дает ровно n значений корня. Они нах. По ф-ле

(пример) -?

|i|=1;

k=0,1,2.

Все корни явл.вершинами прав.n-уг.,впис.в окр.с центром в т O(0,0)и

М6,7 - 2.Система линейных ур-ий.

Опр.Линейным ур-ем с переменными х1,x2,…,xn назыв.уравн вида

Где а1,..,аn-действ.коэф

Аixi-i-ый член ур-я

Xi-переменные, b-своб.член

Опр. Системой m линейных ур-й (слу)назыв.их конъюнкция из m-уравнений с n-неизвестными

Таблица, составл-я из коэф-в, наз-ся матрицей системы (гл диагональ). Расширенная матрица (=b1…).

Решением системы наз любой упоряд набор чисел, при подстановке кот вместо неизвестных каждое уравн системы обращается в верное числовое равенство.)Решить систему - значит, найти все ее решения (в случае неопределенной системы - дать формулу общего решения) или доказать ее несовместность. Однородная слу всегда совместна и имеет хотя бы одно решение x₁ = ... = x_m = 0. Это решение не всегда единственно.

Две системы равнос-ны, если мн-ва их решений совпадают.

Если система имеет решения, то она совместна.

Одно решение-определенная система, много-неопредел-я.

Элемен преобраз слу являются следующие: 1) умножение уравнения на любое число, отличное от нуля; 2) прибавление к одному из уравнений другого, умноженного на число

Т:если к системе прим-ть элем-е преоб-я, то получится система, равносильная данной.

Док

Опр.Главным членом лин.ур-я называется первый ненулевой член ур-я. Переменная в этом члене называется главной переменной.

Опр. Система ненул.лин ур-ий назыв.ступенчатой, если в ней нулевые строки ниже остальных, гл.член каждого послед.ур-я наход-ся правее гл.члена предшеств.ур-я.

Т: всякую ненулевую СЛУ можно привести к ступ.виду с помощью. эл.преобр.

Треугольная система (вид), частный сл-й ступенчатой.

МЕТОД ГАУССА. Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элемен преобраз в эквивалентную систему ступенчатого треугольного вида. Полученная система содержит все неизвестные в первом уравнении. Во втором урав отсутствует первое неизвестное, в третьем уравн отсутствуют первое и второе неизвестные и т. д. Если система совместна и определена (един решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно - предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы. Пример:

Ответ:

Ситуации решения СЛУ методом Гаусса: 2 случая

1)расш-я матрица имеет строку (0 0 ..0=b) b<>0, -противоречивая строка. Соотв-ее Ур-е реш-й не имеет, значит система не совместна. 2)кол-во ур-ий в ступ.виде равно кол-ву переменных(СЛУ определена(имеет ед.решение)3)в ступ.виде кол-во ур-ий < кол-ва переменных(СЛУ не определена)выражаем главные через свободные.эти выражения наз-ся общим решением(бескон.много решений).

Однородная система всегда совместна, реш (0..0).

Т:если число уравнений ЛОС меньше числа переменных, то система имеет не нулевое решение.

М6,7 - 3.матрицы и определители.

Матрицей размерности m x n наз-ся прям-я таблица чисел из m строк и n ст-в A= где aik- элементы матрицы.

Опр. 2 матрицы считаются равными,если равны все их соответсвтенные элементы

Опр.суммой 2х матриц назыв.матрица, каждый элемент которой равен сумме соответсвующих элементов данных матриц. Для матриц одинак-х размеров.

Пример

Опр.Произведением числа на матрицу А называется матрица: А.

Опр.Пусть дана строка и столбец одинаковой длины. Произведением строки на столбец называют сумму произведений соответсвующих элементов.

Опр.Пусть дана матрица А размера m×n и матрица В размера n×t. Произведением матрицы A на В называется матрица С размера m×t.

A×B=C=где сij-произ.i-ой строки А на j-столбец В. Прим.

Транспонирование – операция, меняющая в матрице местами строки и столбцы. Свойства операций над матрицами:

1)Кмм+ (a+b=b+a)

2)Acc+ (A+B)+C = A+(B+C)

3)нейтр. Эл. A+O = O+A =A;

4)против.матр. A+(-A)=(-A)+A=O.

Т.о.по сложению матрицы обр. Абелеву группу

5)АСС* (ав)с=а(вс) док-во

6)ДИС*а(в+с)=ав+ас и (а+в)с=ас+вс

7)с(А1+А2)=сА1+сА2

Опр. Пусть дана матрица n*n.

Определителем А наз-ся число |А| =

Подстановка (сигма)-взаимноодн. Отобр-е мн-ва на себя. Кол-во – n факт-л. Сигма четная, если число инверсий четно.

Формулы для n=2;3.

Свойства определителей.

1)det треуг .матрицы = произвед. диагон.элементов.

2)det не меняется при транспонировании

3)если в det поменять местами 2 строки, не трогая остальные, то он изменит знак на противоположный

3)Общий множитель элементов строки det можно вынести за знак det

4)если некоторая строка det равна сумме 2х слагаемых, то det равен сумме 2х det,в первом из которых эта строка равна первому слагаемому, а во втором-втрому

5)det с 2мя одинаковыми строками равен 0

6)det, содержащий нулевую строку равен 0 док-во

7)если к строке det,прибавить др. строку, умнож.на число, то det не изменится.

9)если одна из строк – лин-я комбин-я других строк, то det=0.

10)det, содержащий 2 пропорц строки равен 0. док-во

Опр.если в det вычеркнуть iую строку и k-ый столбец, на пересечении которых наход-ся элемент a_ik, то оставшийся det называется минором эл-та a_ik и обозн.М_ik

Опр.выражение A_ik=(-1)^i+k М_ik наз.алгебраич.дополнением эл-та a_ik

₍алг.доп-е эл-та det –это минор этого эл-та,умнож на -1 в степени, равной сумме номеров вычеркнутой строки и столбца.

Пример.

Т: пусть дан det

Где -алгебр.дополн. эл-ов ,составляющих k-ый столбец.(**)-разложение по k-му столбцу.

Разложение det по i-ой строке:

Прим разложим det по 3 строке:

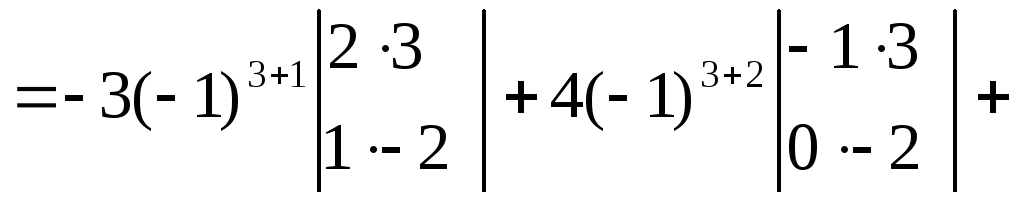
Прим.разложим det по 1му столбцу

Правило Крамера: пусть дана система Ax=b, число уравнений= кол-ву неизвестных. Det<>0. Тогда система имеет единственное решение по формулам: x1=det1/det …

Det I – опред-ль, получ-й из det заменой i-го столбца на столбец свободных коэф-в.

Опр.Пусть А-кв.матрица порядка n. Матрицей, обратной к А называется матрица, обозначаемая A^-1 ,для кто.вып.условие:

Опр. единичная матрица - квадратная матрица, все диагональные элементы кот единицы, а остальные – нули.

Опр.Матрица называется обратимой, если для неё сущ.обратная матр.

Опр.Матрица наз-ся невырожденной, если det<>0.

Т:А обратима  когда А невырожденная.

Опр.Матрица А*, составленная из алгебр-х дополнений, записанных по столбцам – соединенная. А11 Аn1

А12 Ann

Основное св-во – АА*=А*А=

(по главной диагонали)