Процесс ортогонализации.

Зададимся целью из произвольного базиса ВП построить ортонормированный. Разобьём задачу:

1. Из произвольного базиса построим ортогональный.

2. Нормируем полученный базис.

Рассмотрим произвольный базис (a₁,a₂,…,a_n) евклидова ВП. Построим ортогональный базис b₁,b₂,…,b_n.

1. Положим b₁=a₁

2. Положим b₂=₁b₁+a₂. ₁ найдём из условия ортогональности векторов

(b₁,b₂)=0;(b₁,₁b₁+a₂)=0₁=-(b₁,a₂)/(b₁,b₁). Подставив ₁ в b₂ найдем вектор b₂.

3. предположим построена система b₁,b₂,…,b_i , для всякого I b_i – лин-я комб-я векторов a₁,a₂,…,a_i . Это предположение будет выполняться для b_l+1

(Альфа)I подбираем из условия ортогональности b_l+1 ко всем векторам b_i i-=1…l. Т.к. b₁,b₂,…,b_l ортогональны между собой:

получаем

Этот процесс конечен, состоит из n шагов, он позволяет получить ортогональный базис, который можно нормировать.

Опр:Вектор наз. нормированным (единичным), е/и его скалярный квадрат =1.

Опр. Если а<>0, то нормированием вектора а наз-ся переход к вектору

Опр Базис наз. ортонормированным, если все векторы в нём попарно ортогональны и каждый вектор ортонормирован:

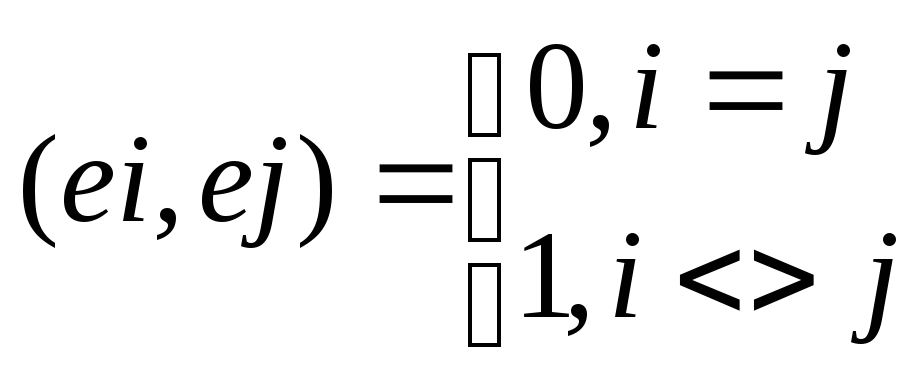
След-е. всякое евклидово пространство обладает ортонормированным базисом.

М6,7 - 5. Группы (гр.), кольца и поля.

Опр. Мн-во G с одной бинарной (отображение х*х=>х) алгебр-кой операцией <G,∙> наз-ся группой, если выполн-ся след-щие условия (аксиомы):

1. (a,bG) a(bc)=(ab)c

2. (eG)( aG) ae=ea=a (сущ-ние нейтр-го эл-та)

3. (aG)( bG) ab=ba=e (сущ-ние для кажд. эл-та ему обратного)

Пр-р: <Z,+>, <2Z,+>, <Q,+>, <R,+> <[-1;1],*>.

Простейшие св-ва.

1. Нейтр-й эл-т в гр. единств-й. Док. Пусть в группе 2 нейтр-х эл-та е1 и е2. Тогда выполняется е2*е1=е2 и е1*е2=е1. След-но, е1=е2.

2. Обратный эл-т для любого эл-та a G единств-й. Док. Пусть для элемента а 2 противоп-х а1, а2. а*а1=1 и а2*а=1. Так как а2*а*а1=а2(а*а1)=

=а2*1=а2 и а2*а*а1= (а2*а)*а1=1*а1=а1, то а1=а2.

3. В гр. <G,∙> однозначно разрешимы ур-я ax=b и xa=b a, bG.

Док-во. Док-м, что ур-ния имеют только по одному корню. Пусть x₀ – корень ax=b, т.е. ax₀=b – истина. Тогда сущ-ет a^-1 G такое, что

aa^-1=a^-1a=e, a^-1ax₀=a^-1b

ex₀=a^-1b , т. е. x₀=a^-1b

Подстановкой убеждаемся, что

a^-1b – действ-но корень ур-ния ax=b. Выр-е a^-1b показывает, что этот корень единств-й. Анал-но док-ся, что ур-ние xa=b имеет корень и притом только один.

Группы преобразований

Пусть М – произвольное мн-во (конечное или бесконечное). Преобраз-ем мн-ва М наз-ся биективное отобр-е мн-ва М на себя.

Мн-во S(M) всех преобраз-й М образует гр. относ-но операции композиции (вместо умножения) отобр-й мн-ва М, т. к. композ-я любых отобр-й есть снова отобр-е, композиция преобраз-й – снова преобраз-е. Композиция преобраз-й ассоциативна. Роль единичного эл-та в группе преобраз-й играет тождеств-е преобраз-е, т.е. ε(x)=x. Известно, что преобраз-е, как биективное отображ-е, обратимо. Обратное отображ-е будет снова преобраз-м мн-ва М.

Пример – группа симметрий квадрата (4 поворота и 4 осевые симметрии).

Опр. Пусть G, G’ - гр. Отобр-е φ гр. G на гр. G’ наз-ся изоморфизмом гр. на гр., если

1. φ биективное отображ-е

2. φ сохраняет операцию в гр. G, т. е. a,bG φ(a*b)=φ(a)*φ(b)

Пример: G – мно-во целых чисел, G’ – мн-во четных целых чисел. Ф(а)=2а.

Опр. Гр. G наз-ся изоморфной гр. G’, если сущ-ет хотя бы один изоморфизм f гр. G на гр. G’.

Опр. Пусть Н – непустое подмн-во G и Н замкнуто относит-но операции умножения, определ-й в G. Если Н само явл-ся группой, то оно наз-ся подгруппой G.