15. На телефонной станции неправильное соединение происходит с вероятностью 0,003.

Найти вероятность того, что среди 100 соединений произойдет:

а) ровно 5 неправильных соединения;

б) больше трех неправильных соединений.

16. Случайная величина задана функцией плотности распределения

⎧ 0, x < 0

_⎪

^{p ( x ) = ⎪ x , 0 ≤ x < 2 2}

^⎨ ₄

^⎪

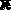
^⎪_⎩ ^{0, x ≥ 2 2.}

Найти функцию распределения

F ₍ x ₎

случайной величины X . Построить графики

функций

_{p ( x ) и}

_{F ( x ) . Вычислить для этой случайной величины математическое}

ожидание, дисперсию, среднее квадратическое отклонение, моду и медиану.

_{17. Случайная величина X задана функцией распределения}

_{⎧ 0, x < 0}

_{F ( x ) =} ^⎪_ax² _{, 0 ≤ x < 1}

_⎨

Найти а) параметр a ;

б) плотность распределения

_⎪

^⎩

_{p ( x ) ;}

^{1, x ≥ 1.}

в) вероятность того, что в результате одного испытания случайная величина X

^{примет значение из интервала (0, 5; 2, 5) ;}

г) математическое ожидание и дисперсию данной случайной величины;

д) вероятность того, что в результате 400 независимых испытаний случайная

величина X примет 320 раз значение из интервала (0,5; 2,5) .

18. Случайная величина X распределена равномерно на отрезке _[1, 3; 3, 7_] . Найти выражения для плотности распределения и функции распределения этой случайной величины. Вычислить математическое ожидание и дисперсию случайной величины X .

19. Случайная величина распределена по показательному закону с параметром 3,2. Записать выражения для плотности распределения и функции распределения этой случайной величины. Построить их графики. Вычислить математическое ожидание и дисперсию случайной величины X .

20. Случайная величина распределена по нормальному закону с параметрами

Найти вероятность того, что эта случайная величина примет значение

а) из промежутка [0; 10];

б) меньшее 8;

_{в) большее 5;}

^{a = 5}

^{и σ = 4 .}

г) отличающееся от своего среднего значения по абсолютной величине не более чем на 6.

21. Масса пойманной рыбы подчиняется нормальному закону с

M ₍ X ₎ = 375 г и σ ₍ X ₎ = 25 г.

Найти вероятность того, что масса одной пойманной рыбы составит не более 450г.

22. По выборке А решить следующие задачи:

а) составить вариационный ряд, построить полигон и гистограмму;

б) вычислить относительные и накопленные частоты,

в) построить эмпирическую функцию распределения и ее график,

г) вычислить числовые характеристики вариационного ряда: выборочную среднюю, дисперсию, среднее квадратическое отклонение, моду, медиану.

_{д) при уровне значимости}

_{α = 0, 05}

_{проверить гипотезу о распределении}

_{Пуассона соответствующей генеральной совокупности.}

Выборка А:
	3	3	1	0	0	3
	5	3	3	0	2	3
	0	0	4	1	5	1
	6	5	4	7	4	2
	2	4	3	4	5	4
	7	4	0	5	6	3
	5	4	1	3	3	6
	3	1	1	5	2	3
	5	3	3	4	1	5
	6	1	3	3	5	6

23. По выборке В решить следующие задачи:

а) составить вариационный ряд,

б) вычислить относительные и накопленные частоты,

в) построить эмпирическую функцию распределения и ее график,

г) вычислить числовые характеристики вариационного ряда: выборочную среднюю, дисперсию, среднее квадратическое отклонение, моду, медиану.

_{д) при уровне значимости}

_{α = 0, 05}

_{проверить гипотезу о нормальном}

распределении соответствующей генеральной совокупности.

Выборка В:

58	78	84	62	63	10	55	90
102	70	66	89	71	92	71	93
83	42	110	110	56	96	95	87
88	102	104	88	64	96	92	67
78	95	71	105	50	66	73	76
100	72	86	46	102	95	98	84
82	46	60	94	109	93	79	74
62	97	94	91	81	71	89	78
85	80	93	64	65	109	89	55
103	98	108	68	65	71	82	70