1.2.1.6 Поверочный расчет топки

Максимальная температура горения

, (1.20)

.

Температура продукта на входе в камеру радиации равна t₁ = 250 ⁰С.

Принимается средняя температура наружной стенки труб на 30 ⁰С выше средней температуры продукта в камере радиации:

, (1.21)

.

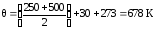Коэффициент теплоотдачи конвекцией

, (1.22)

.

Определяются все величины, необходимые для расчета эквивалентной абсолютно черной поверхности.

Количество тепла, переданное конвекцией в топке:

, (1.23)

.

Потери тепла через стенки топки

, (1.24)

.

Температура газа в топке для практических расчётов

(1.25)

где С_pm – средняя теплоёмкость газов в пределах температур от Т_Р и Т_V (практически можно принять при Т_Р); Q_PK – количество тепла, переданное конвекцией от газов к трубному экрану, кВт; Q_ПОТ – потери тепла через стенки топки, кВт.

При определении величины _V можно пользоваться приближённым уравнением

(1.26)

Угловой коэффициент определяется по методике [2],  = 0,56.

Суммарная поверхность кладки

F = 2lb + 2lh + 2hb = 2182,1 + 2188,4 + 28,42,1 = 413,8 м².

Таблица 1.11 - Основные размеры камер

Величина	Камера радиации
Длина	18 м
Ширина	2,1 м
Высота	8,4 м

Неэкранированная поверхность кладки (потолочные стенки и под печи)

F = 2lb + 2lh` = 2188,4 + 2184,6 = 241,2 м².

Величина углового коэффициента взаимного излучения экрана и кладки

, (1.27)

Величина ₁ определятся по следующему уравнению

(1.28)

где _H, _F - соответственно степень черноты трубного экрана, неэкранированной поверхности кладки в топке. Для расчётов можно принять _H = _F = 0,9.

Величина определяется по уравнению

(1.29)

Величина А₁ определяется по уравнению

(1.30)

Величина эквивалентной абсолютно черной поверхности

, (1.31)

Температурная поправка теплопередачи в топке определяется как

(1.32)

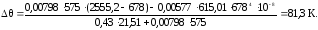
Аргумент излучения определяется по уравнению

, (1.33)

.

Характеристика излучения

, (1.34)

Температура дымовых газов на выходе из топки

,

.

Общая длина L_р реакционного змеевика определяется по формуле

, (1.35)

где L –длина одной трубы, м; F_тр – поверхность (наружная) одной трубы, м².

.

Однако для реакционно-нагревательных печей, какими являются печи крекинга, длина реакционных труб должна быть достаточна для превращения сырья с заданной глубиной:

, (1.36)

где W - средняя линейная скорость движения парожидкостной смеси в реакционных трубах, м/с. Определяется по выражению (1.37); продолжительность пребывания сырья в реакционной зоне, с.

, (1.37)

где _с - плотность сырья при 20 ⁰С, кг/м3; _пж - плотность парожидкостной смеси в реакционных трубах, кг/м3.

Для условий на выходе из печи можно рассчитать, что

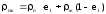, (1.38)

где _п, _ж - плотность паровой и жидкой фаз при температуре и давлении на выходе из печи, кг/м³; е – доля отгона на выходе из печи.

,

Продолжительность пребывания сырья в реакционной зоне рассчитывается на основании опытных данных. Кинетика реакции висбрекинга удовлетворительно описывается уравнением скорости реакции первого порядка

, (1.39)

где К – константа скорости реакции первого порядка, с^-1.

Из кинетического уравнения реакции определяется продолжительность крекинга для принятых значений констант скорости реакции и глубины крекинга X₁ сырья в печи. Константа скорости определяется графически [1] и составляет К=610^-3с^-1.

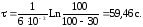
Тогда длина реакционного змеевика составляет