
7УМК
.PDF
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Государственное образовательное учреждение высшего профессионального образования
"УФИМСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЯНОЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ" (УГНТУ)
Кафедра математики
УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС
дисциплины «Математика»
________________________________________________________________________________
РАЗДЕЛ 7 «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ»
Теоретические основы Методические указания для студентов Материалы для самостоятельной работы студентов
Уфа 2010

ИНФОРМАЦИЯ ОБ АВТОРАХ ИНФОРМАЦИЯ О РЕЦЕНЗЕНТАХ АННОТАЦИЯ 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
1.1. Двойной интеграл 1.1.1. Определение двойного интеграла. Его геометрический смысл
1.1.2. Свойства двойного интеграла
1.1.3. Вычисление двойного интеграла
1.1.3.1.Понятие о правильных областях. Двукратный
интеграл
1.1.3.2.Сведение двойного интеграла к двукратному
1.1.3.3.Замена переменных в двойном интеграле. Вычисление двойного интеграла в полярных координатах 1.1.4. Приложения двойных интегралов к задачам геометрии и механики
1.1.4.1.Вычисление объемов тел и площадей плоских областей
1.1.4.2.Задачи механики 1.2. Тройной интеграл
1.2.1. Определение тройного интеграла. Его механический смысл. Свойства 1.2.2. Вычисление тройного интеграла
1.2.2.1.Вычисление тройного интеграла в декартовых координатах
1.2.2.2.Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах 1.2.3. Приложения тройных интегралов к задачам геометрии и механики
1.2.3.1.Вычисление объемов тел
1.2.3.2.Задачи механики 1.3. Криволинейные интегралы
1.3.1. Криволинейный интеграл первого рода (или по длине дуги)
1.3.1.1.Определение и физический смысл криволинейного интеграла первого рода. Свойства
1.3.1.2.Вычисление криволинейного интеграла первого рода
1.3.1.3.Криволинейный интеграл для пространственного
случая
1.3.1.4.Некоторые применения криволинейного интеграла первого рода

1.3.2. Криволинейный интеграл второго рода (или по координатам)
1.3.2.1.Задача о работе силового поля. Определение криволинейного интеграла второго рода
1.3.2.2.Существование и вычисление криволинейного интеграла второго рода
1.3.2.3.Связь между криволинейными интегралами первого и второго рода
1.3.2.4.Формула Грина
1.3.2.5.Условия независимости интеграла от пути интегрирования
1.3.2.6.Вычисление площади с помощью криволинейного интеграла второго рода 1.4. Поверхностные интегралы
1.4.1.Поверхностный интеграл первого рода (или по площади поверхности). Теорема существования интеграла
1.4.1.1.Вычисление поверхностного интеграла первого рода
1.4.1.2.Некоторые применения поверхностного интеграла первого рода 1.4.2. Поверхностный интеграл второго рода (или по координатам)
1.4.2.1.Вычисление поверхностного интеграла второго рода
1.4.2.2.Применение поверхностного интеграла второго рода 2. МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ Введение 2.1. Кратные интегралы
2.1.1. Вычисление двойного интеграла в декартовой системе координат
2.1.2. Вычисление двойного интеграла в полярной системе координат
2.1.3. Приложение двойных интегралов к вычислению площадей плоских фигур
2.1.4. Приложение двойных интегралов к вычислению объемов цилиндрических тел
2.1.5. Приложение двойного интеграла. (К вычислению массы, центра тяжести и момента инерции)
2.1.6. Вычисление тройного интеграла в декартовой системе координат
2.1.7. Вычисление тройного интеграла в цилиндрических и
сферических координатах 2.1.8. Приложение тройных интегралов к вычислению объемов
тел 2.1.9. Приложения тройных интегралов к вычислению массы,
центра тяжести и момента инерции тела 2.2. Криволинейные интегралы
2.2.1. Криволинейные интегралы первого рода или по длине дуги, их вычисление
2.2.2. Применения криволинейного интеграла первого рода 2.2.3. Криволинейные интегралы второго рода или по
координатам, их вычисление 2.2.4. Формула Грина
2.2.5. Применения криволинейного интеграла второго рода 2.3. Поверхностные интегралы
2.3.1. Поверхностные интегралы 1-го рода или по площади поверхности, их вычисление
2.3.2. Приложения поверхностных интегралов первого рода 2.3.3. Поверхностные интегралы второго рода или по
координатам, их вычисление
3. МАТЕРИАЛЫ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
3.1. Контрольные вопросы 3.2. Задачи и упражнения для самостоятельной работы 3.3. Расчетные задания Список литературы
АВТОРЫ:
Бахтизин Р.Н., Акмадиева Т.Р., Умергалина Т.В., Шамшович В.Ф., Аносова Е.П., Байрамгулова Р.С., Галиуллин М.М., Галиева Л.М., Галиакбарова Э.В., Гимаев Р.Г., Гудкова Е.В., Егорова Р.А., Жданова Т.Г., Зарипов Э.М., Зарипов Р.М., Исламгулова Г.Ф., Ковалева Э.А., Майский Р.А., Мухаметзянов И.З., Нагаева З.М., Савлучинская Н.М., Сахарова Л.А., Степанова М.Ф., Сокова И.А., Сулейманов И.Н., Фаткуллин Н.Ю., Хайбуллин Р.Я., Хакимов Д.К., Хакимова З.Р., Чернятьева М.Р., Юлдыбаев Л.Х., Якубова Д.Ф., Якупов В.М., Янчушка А.П., Яфаров Ш.А.
8 – (347)2428715
E-mail: kafedra-matematiki@rambler.ru
РЕЦЕНЗЕНТЫ:
Кафедра программирования и вычислительной математики Башкирского государственного педагогического университета.
Заведующий кафедрой д. ф.-м. наук, профессор Р.М. Асадуллин.
Кафедра вычислительной математики Башкирского государственного университета.
Заведующий кафедрой д. ф.-м. наук, профессор Н.Д. Морозкин.
АННОТАЦИЯ
Учебно-методический комплекс дисциплины «Математика». Раздел 7 «Интегральное исчисление функции нескольких переменных». Теоретические основы. Методические указания для студентов. Материалы для самостоятельной работы студентов.
В разделе «Теоретические основы» и «Методические указания для студентов» содержатся необходимые для изучения дисциплины «Математика», в объеме, предусмотренном ГОС для технических вузов, теоретический материал, способы и методы решения практических задач.
Раздел «Материалы для самостоятельной работы студентов» включает в себя: контрольные вопросы, задачи и упражнения для самостоятельной работы, расчетные задания, лабораторные работы, литературу.
Представлен перечень контрольных вопросов для контроля знаний, полученных студентами при изучении теоретических и методических основ дисциплины. Задачи и упражнения для самостоятельной работы студентов позволяют учащимся индивидуально во внеурочное время контролировать уровень усвоения материала по данной дисциплине.
Расчетные задания содержат задания для студентов, позволяющих отработать навыки решения задач практического содержания.
В разделе «Лабораторная работа» представлен теоретический материал, последовательность проведения лабораторной работы и данные для проведения лабораторной работы по вариантам.
При изучении дисциплины обеспечивается фундаментальная подготовка студента в области применения математики, происходит знакомство со стержневыми проблемами прикладной математики, базовыми приложениями, навыками и понятиями, обязательными для прочного усвоения последующих дисциплин и практического использования полученных знаний в решении конкретных задач, которые ставятся перед инженером.
Учебно-методический комплекс разработан для студентов, обучающихся по всем формам обучения по направлениям подготовки и специальностям, реализуемым в ГОУ ВПО УГНТУ.
© Уфимский государственный нефтяной технический университет, 2010
УЧЕБНО - МЕТОДИЧЕСКИЙ КОМПЛЕКС
РАЗДЕЛ 7 «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ»
1. Теоретические основы
1.1.ДВОЙНОЙ ИНТЕГРАЛ
1.1.1.Определение двойного интеграла. Его геометрический смысл
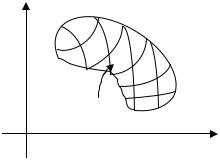
Пусть в некоторой замкнутой области D на плоскости xOy задана ограниченная функция двух переменных z = f (x, y). Проделаем следующие операции (подобно тому, как это делаем при определении определенного интеграла).
1. Область D (рис. 1.1) разобьем |
произвольным образом на n частей |
||||||||||||||||
S1 , S2 ,.... |
Sn . |
И чтобы не вводить новых |
символов, |
площади этих |
|||||||||||||
|
|
|
|
|
Si (i = |
|
), а |
|
|||||||||
подобластей тоже |
будем обозначать |
через |
1, n |
диаметры их |
|||||||||||||
(расстояния между наиболее удаленными точками границы области |
|
Si ) – |
|||||||||||||||
y |
|
|
через |
di . |
Пусть |
max di |
- наибольший |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Si (i = |
|
). |
|
|
|
|
||||||
|
|
Pi |
диаметр областей |
1, n |
|
|
|
|
|||||||||
|
D |
Si |
|
|
|||||||||||||
|
|
2. |
В каждой из областей |
|
возьмем |
||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
произвольную точку Pi (ξi , ηi ) (внутри или |
|||||||||||||
|
|
|
|
||||||||||||||
|
Si |
|
|
на |
границе |
Si ). |
И вычислим значение |
||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
||||||||||||||
0 |
|
|
|
x функции в этой точке |
f (P ) = f (ξ |
i |
, η |
i |
). |
||||||||
|
|
|
|
|
|
Значение f (Pi ) |
i |
|
|
|
|||||||
|
Рис. 1.1 |
|
3. |
умножим на площадь |
|||||||||||||
|
|
|
|
Si |
- |
меру элементарной области |
|
Si . (В |
|||||||||
случае функции одной переменной y = f (x) мерой элементарной области была длина x i отрезка [x i−1 , x i ], в случае функции двух переменных за меру области Si принимается ее площадь).
4. Составим сумму произведений вида f (Pi ) Si :
n
Sn = f (P1 ) S1 + f (P2 ) S2 + ... + f (Pn ) Sn = ∑ f (Pi ) Si (1.1)
i=1
Сумма (1.1) называется интегральной суммой для функции z = f (x, y) по области D, соответствующей данному разбиению.
При заданном числе n частей Si , на которые дробится область D, можно составить сколько угодно интегральных сумм: во-первых, по-разному дробить фигуру на n частей, а во-вторых, в каждой части можно произвольным образом выбирать точку Pi .
5. Измельчая разбиение, находим предел I интегральной суммы Sn при условии, что max di → 0 , следовательно, n → ∞
I = lim S |
n |
= |
lim |
∑n |
f (P ) |
S |
i |
. |
max di →0 |
|
max di →0 |
i=1 |
i |
|
|
||
|
|
|
|
|
|
|||
(n→∞) |
|
|
(n→∞) |
|
|
|
|
ОПРЕДЕЛЕНИЕ. Если существует конечный предел интегральной суммы Sn при max di → 0 (при этом n → ∞) и если этот предел не зависит ни от способа разбиения области D на элементарные площадки Si , ни от
выбора точки Pi Si , то он называется двойным интегралом |
от функции |
|||||
z = f (x, y) по области D и обозначается символом |
|
|||||
|
∫∫ f (P)dS |
или |
∫∫ f (x, y)dxdy . |
|
||
|
D |
|
D |
|
|
|
Выражение |
f (x, y)dxdy |
называется |
подынтегральным |
выражением; |
||
функция f (x, y) |
- подынтегральной функцией; dS = dxdy |
- элементом |
||||
площади; D – областью интегрирования; х и у – переменными интегрирования. |
||||||
Итак, по определению |
|
|
|
|
|
|
|
∫∫ f (P)dS = |
lim |
∑n |
f (Pi ) Si . |
(1.2) |
|
|
D |
max di →0 |
i=1 |
|
|
|
|
(n→∞) |
|
|
|||
Функция, имеющая предел (1.2), называется интегрируемой в области D. Вводя определение двойного интеграла, мы предполагали, что функция z = f (x, y) ограничена в области D. Однако не всякая ограниченная функция
интегрируема, иначе говоря, имеет двойной интеграл. Какие условия надо наложить на функцию еще, чтобы можно было гарантировать существование двойного интеграла? Ответ на этот вопрос дает
Теорема существования двойного интеграла. Всякая функция z = f (x, y), непрерывная в ограниченной замкнутой области D, интегрируема в
этой области. |
|
|
|
|
|
|
|
|
|||
Выясним теперь геометрический смысл двойного интеграла. |
|
|
|||||||||
|
z |
|
|
|
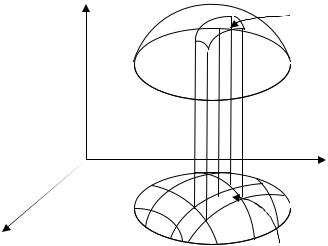
Рассмотрим |
|
в |
||||
|
|
z = f (x, y) |
пространстве |
тело |
Т, |
||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
ограниченное |
снизу |
областью |
|||
|
|
|
|
|
|
D, |
сверху |
поверхностью |
|||
|
|
|
|
|
|
z = f (x, y) такой, что функция |
|||||
|
|
|
|
|
|
f (x, y) |
непрерывна |
и |
|||
|
|
|
Ti |
|
|
неотрицательна в области D, с |
|||||
0 |
|
|
|
Т |
|
||||||
|
|
|
|
|
|
– |
|
|
|
||
|
|
|
|
y |
боков |
цилиндрической |
|||||
|
|
|
|
|
поверхностью |
с образующей, |
|||||
|
|
|
Pi |
|
|
параллельной |
оси |
Oz, |
и |
||
|
|
D |
|
|
направляющей |
– |
границей |
||||
x |
|
|
|||||||||
|
|
области D (рис. 1.2). Такое тело |
|||||||||
|
Рис. 1.2 |
|
Si |
||||||||
|
|
будем |
|
|
называть |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
цилиндрическим. |
|
|
|||
Поставим задачу: найти объем V цилиндрического тела. При разбиении |
|||||||||||
основания цилиндрического |
тела – области |
D – |
на |
n частей |
Si тело |
Т |
|||||
окажется разбитым на n элементарных цилиндрических тел – столбиков
Т1 , Т2 ,..., Тn |
с основаниями |
S 1 , |
S 2 , ... , |
|
S n . |
Объем цилиндрического |
|
столбика |
Тi |
приближенно равен объему прямого цилиндра с тем же |
|||||
основанием и высотой f (Pi ): |
|
|
|
|
|
||
|
|
Vi ≈ f (Pi ) Si . |
|
|
|
||
Принимая объем V данного цилиндрического тела Т приближенно равным |
|||||||
объему Vn |
n – |
ступенчатого тела, получаем приближенное равенство |
|||||
|
|
V ≈ V |
= ∑n |
f (P ) S |
i |
, |
(1.3) |
|
|
n |
i=1 |
i |
|
|
|
|
|
|
|
|
|
|
|
которое, интуитивно ясно, будет тем ближе к точному, чем меньше размеры
областей |
Si |
и больше n. Для получения |
точного |
значения |
V нужно в |
|||||||
выражении (1.3) перейти к пределу, устремив наибольший диаметр di |
ячеек |
|||||||||||
Si к нулю: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = lim V |
= |
lim |
∑n |
f (P ) |
S |
i |
. |
|
|
|
|
|
max di →0 |
n |
max di →0 |
i=1 |
i |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
(n→∞) |
|
|
(n→∞) |
|
|
|
|
|
|
|
Последний предел есть двойной интеграл, значит, |
|
|
|
|
|
|||||||
|
|
V = ∫∫ f (x, y)dxdy . |
|
|
|
|
(1.4) |
|||||
|
|
|
D |
|
|
|
|
|
|
|
|
|
Таким образом, решена задача об объеме цилиндрического тела и |
||||||||||||
установлен |
геометрический смысл |
двойного интеграла: двойной интеграл |
||||||||||
∫∫ f (x, y)dxdy |
от неотрицательной |
функции f (x, y) |
дает |
объем |
||||||||
D
соответствующего цилиндрического тела, верхней поверхностью которого служит поверхность z = f (x, y).
1.1.2. Свойства двойного интеграла
Как видно, конструкции определенного интеграла и двойного интеграла аналогичны. Вследствие этого свойства, а также доказательства свойств двойного интеграла аналогичны соответствующим свойствам определенного интеграла. Поэтому приведем свойства двойного интеграла, не останавливаясь на доказательствах. Свойства формулируются в предположении непрерывности функций.
10 . Двойной интеграл от суммы конечного числа функций равен сумме двойных интегралов от слагаемых функций
∫∫[f1 (x, y) + f 2 (x, y) + ... + f n (x, y)]dS =
D
= ∫∫ f1 (x, y)dS + ∫∫ f 2 (x, y)dS + ... + ∫∫ f n (x, y)dS.
D D D
20 . Постоянный множитель подынтегральной функции можно выносить за знак интеграла
