7УМК

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

используем формулу (2.17): J 2 =

(x + y + z +1)

.PDF

Скачиваний:

Добавлен:

17.03.2015

Размер:

2.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1710 11 12 13 14 15 16 17 > Следующая >>>

Решение. а) Поскольку область V (рис. 2.21) правильная вдоль оси 0Z, то для вычисления интеграла используем формулу (2.16):

	1			∫∫			1−x− y					1							∫∫	1			dxdy(z		1−x−y	)=
							1−x− y					1								1					1−x−y
									∫																0
J		=			dxdy											dz		=
			Dxy				0 1				- x - y						Dxy 1 - x - y
			Dxy				0 1				- x - y						Dxy 1 - x - y
																				1			1−x	1
= ∫∫					1			× (1 - x - y)dxdy =											∫∫ dxdy = ∫ dx ∫ dy						= ∫ dx(y			10−x )=
					1

		Dxy	1 - x - y																Dxy	0			0	0
		1									x	2		1			1
		1										2		1
= ∫ (1 - x)dx =										-					=			Здесь область D xy есть треугольник
																	.
									x								.
		0									2			0			2
						z								0									z
																							z

																							B
						1																	3
						1
													z = 1 − x − y								C		2					y = 3 − z
													z = 1 − x − y								C		1
																							1
						0											1						0	1		2	3

																				y
																	B
																	B
			A								y = 1 − x
											y = 1 − x										A



			1
			1																			2
	x								Рис. 2.21											x			Рис. 2.22
																							Рис. 2.22

AOB .

б) Поскольку область V (рис. 2.22) правильная вдоль оси 0Y, то

=			3−z
=	∫∫ dxdz		∫	(x + z +1 + y)−3d(x + z +1 + y) =
	Dxz		0			y=3−z
			(x	+ z +1 + y)	−2
					−2
=	∫∫ dxdz							=
=	∫∫ dxdz			- 2				=
	Dxz			- 2
						y=0
						y=0
=		(x + z +1 + 3 - z)−2					(x + z +1)−2		=
=	∫∫ dxdz			- 2	-			- 2	=
	Dxz			- 2				- 2

= - 1

= - 1 ∫∫

dxdz -

∫∫ dxdz

2 Dxz

4)2

(x + z +1)2

2 Dxz

(x + z +1)2

= - 1

dxdz = 1

∫∫

∫ dx∫ (x +1 + z)−2 d(x +1 + z) - 1

∫

∫ dz =

2 Dxz

(x + 4)2

(x + 4)2 0

(x +1 + z)−1 3

∫ dx

-1

∫

+ 4)2

∫

0 (x

4 x +1

- 3 ∫2 (x + 4)−2 dx = 1 (- ln x + 4 + ln x +1 ) 2 - 3 × (x + 4)−1 2

2 0

-1

(- ln 6 + ln 3 + ln 4 - ln1) -

ln 2 -

Здесь область D xz есть прямоугольник AOBC.

2.1.7. Вычисление тройного интеграла

в цилиндрических и сферических координатах

Необходимые

формулы

указания

рассмотрим

при

решении

следующих

примеров.

Примеры решения задач

ρ = a

ПРИМЕР 2.15. Вычислить тройной

− a

интеграл:

а)

x2 + y2 = a 2

J1 = ∫∫∫(x 2 + y2 + z 2 )dxdydz,

где

ограничена

поверхностью

3(x 2 + y2 )+ z 2 = 3a 2 .

Рис. 2.23

Решение. Область V, ограниченная

данной поверхностью, есть эллипсоид

вращения (рис 2.23). Его проекцией

Dxy

на плоскость X0Y является круг

x 2 + y2 £ a 2 . В

данном

случае

целесообразно

применить

цилиндрические

координаты. Формулы связи с декартовых и цилиндрических координат в

данном случае имеют вид

y = r × sin j;

x = r × cos j;

z = z .

Подынтегральная функция преобразуется

x 2 + y2 + z 2

= r2 × cos2 j + r2 × sin 2 j + z 2

= r2 + z 2 .

Элемент объема dv = dxdydz переходит в dv = ρ dϕ dρ dz , где r =

;

x'ρ

x'ϕ

x'z

cos j

- r × sin j

J =

sin j

r × cos j

= r × cos2 j + r × sin 2 j = r.

z'ρ

z'ϕ

z'z

Пределы интегрирования по переменной z получим из уравнения

эллипсоида: 3(x 2 + y2 )+ z 2

= 3a 2

3r2 + z 2

= 3a 2

z 2

= 3a 2 - 3r2 ;

z = ±

3(a 2 - r2 ),

где

z1 = -

3(a 2 - r2 )

- нижний предел интегрирования;

z 2

= +

3(a 2 - r2 ) - верхний предел интегрирования. Итак, наш интеграл

J1 = ∫∫∫(x 2 + y2 + z 2 )dxdydz =

3(a 2 −ρ2 )

∫∫ rdjdr

∫

(r2 + z 2 )dz

Dxy

3(a 2 −ρ2 )

−

3(a 2

−ρ2 )

= ∫∫ rdjdr r

3(a 2 −ρ2 )

Dxy

−

(

3(a

- r

))

3(a

- r

∫∫

djdr =

Dxy

2π

32 ∫ dj∫ r(r2

a 2 - r + a 2 - r × (a 2 - r2 ))dr =

2 3a 2 2π

2π

(a 2

- r2 )

d(a

) = - 3a

∫ dj∫

- r

∫ dj

3 2

2π

= 3a

∫ dj

∫ dj =

б)

Вычислить

тройной

интеграл

J 2 = ∫∫∫ y dxdydz , где

V ограничена

поверхностями y =

x 2 + z 2

и y = a ;

a > 0 .

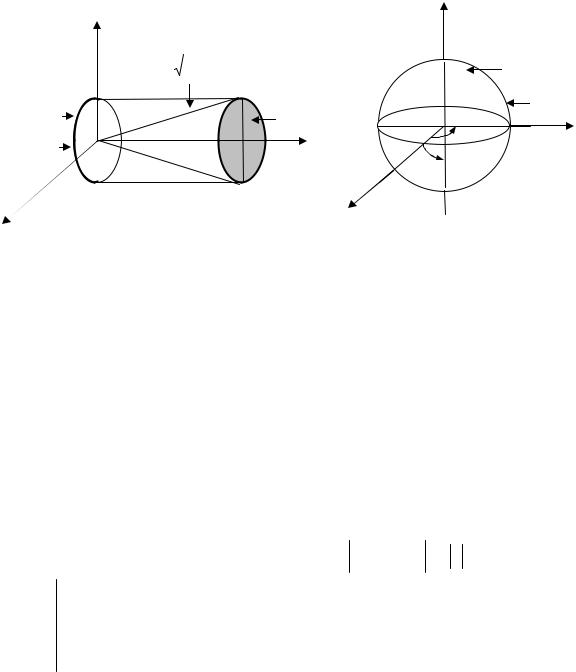
Решение.

Ограниченная данными поверхностями область V есть конус

(рис. 2.24). Эта область правильная вдоль оси 0Y, проекцией этого конуса на

плоскость X0Y является круг x 2 + z 2 £ a 2 , поэтому в данном случае целесообразно применить цилиндрические координаты. Причем формулы связи

декартовых	и цилиндрических координат здесь имеют вид	x = r × cos j;

z = r × sin j;	y = y , тогда уравнение конуса y = x 2 + z 2	= r. Элемент
объема имеет вид: dv = r × djdrdy .

J 2

= ∫∫∫ y dxdydz =

∫∫ rdjdr

∫ y dy =

∫∫ rdjdr

Dxz

2π

= ∫∫

∫ dj∫ (a

r - r

)dr =

∫ dj∫

djdr =

Dxz

2π

a 4

a 4 2π

a 4 2p

pa 4

∫ a

dj =

∫ dj =

4 0

x2 + y2 + z2 = R 2

y = x2 + z2

x2 + z2 = a2

y = a

ρ = R

− R

ρ = a

Dxz

Рис. 2.24

Рис. 2.25

в)

Вычислить тройной интеграл J3 = ∫∫∫(x 2 + y2 + z 2 )dxdydz,

где V –

шар

x 2 + y2 + z 2

£ R 2 .

Решение. Поскольку область интегрирования V есть шар (рис.2.25) и подынтегральная функция состоит из квадратов компонент, в данном случае целесообразно применить переход от декартовых к сферическим координатам. Формулы перехода в этом случае имеют вид x = r × cos j × sin q; y = r × sin j × sin q; z = r × cosq . Подынтегральная функция преобразуется:

x 2 + y2 + z 2 = r2 × cos2 j × sin 2 q + r2 × sin 2 j × sin 2 q + r2 × cos2 q =

= r2 × sin 2 q(cos2 j + sin 2 j)+ r2 × cos2 q = r2 . Элемент объема dv = dx dy dz

принимает вид dv = r2 × sin q × djdrdq , где r2 × sin q = J ,

x'ρ x'ϕ J = y'ρ y'ϕ z'ρ z'ϕ

J3 = ∫∫∫(x 2 +

x'θ		cos jsin q	- r × sin jsin q	+ r × cos jcos q
x'θ		cos jsin q	- r × sin jsin q	+ r × cos jcos q
y'θ	=	sin jsin q	r × cos jsin q	+ r × sin jcos q
z'θ		cos q	0	- rsin q

y2 + z 2 )dxdydz = ∫∫∫r2 × r2 sin q × djdrdq =

2π

ρ5

5 2π

π 2

∫ dϕ∫ sin θdθ ∫

4 dρ

∫ dϕ∫ sin θdθ

∫ dϕ ∫ sin θdθ =

∫ dϕ(− cos θ

0π 2 )= 2R

(ϕ

02π )= 4πR

2.1.8. Приложение тройных интегралов к вычислению объемов тел

Объем пространственной области V с помощью тройного интеграла вычисляется по формуле

V = ∫∫∫dv = ∫∫∫dx dy dz .		(2.18)
V	V

Примеры решения задач

ПРИМЕР 2.16. Вычислить объем тела, ограниченного параболическим

цилиндром 2z = y2 и плоскостями 2x + 3y = 12 ; x = 0 ;

z = 0 (рис. 2.26).

Решение.

Плоскость

2x + 3y = 12

проходит

параллельно

оси

0Z,

пересекается

координатной

плоскостью

X0Y по прямой

2x + 3y = 12

2x + 3y = 12 , с

координатной

плоскостью Y0Z по прямой BC,

B(0;4;0)

цилиндрической

поверхностью

2z = y2

по

y = −

x + 4

AC.

A(6;0;0)

линии

Проекция

получившегося

тела

на

Рис. 2.26

плоскость

X0Y

(область

D xy )

есть треугольник AOB.

По формуле (2.18) искомый объем есть

y2 2

6 −

V = ∫∫∫dxdydz =

∫∫ dxdy

∫ dz =

∫∫

dxdy =

∫ dx

∫

y2 dy =

Dxy

Dxy 2

2 0

−

x +4

∫ dx

∫

−

x + 4

dx =

																																		2								6
																																		2								6
	3		1						2							3				2												-			x +				4						1
																3																-		3	x +				4
																												1						3												(0	- 4)			4		3
= -		×				∫ -						x		+	4		d	-			+ 4				= -																		-								= 16(ед ).
= -		×				∫ -			3			x		+	4		d	-		3	+ 4				= -		4								4								-								= 16(ед ).
	2 6								3											3							4								4									16
																																										0
																																										0
		ПРИМЕР 2.17. Вычислить объем тела, ограниченного параболоидом
вращения z = x 2 + y2 -1 и плоскостью z = 1 (рис. 2.27).
											z																										Решение.													Уравнение
																			z = 1													параболоида														вращения						в
											1								z = 1													цилиндрических																	координатах:
																																z = r2 -1.												Проекция							тела	на
																				z = x2 + y2 − 1												плоскость X0Y есть круг с центром
																																в		начале								координат							и		радиусом,
										0
										0																y						равным								2 , т.е.
																										y						равным								2 , т.е.
																																							x 2 + y2 = (											)2 .
																																							x 2 + y2 = (									2		)2 .
											− 1																					Формулу									(2.18)						переводим					в
																																цилиндрические																	координаты:
																																цилиндрические																	координаты:
x								Рис. 2.27																								V = ∫∫∫dxdydz =
																														2π							V							)dr =

									1																										2
																								1																			2
= ∫∫ rdrdj									∫ dz						= ∫∫ rdrdj(z									ρ2 −1 )= ∫ dj											∫ r(2 - r
= ∫∫ rdrdj									∫ dz						= ∫∫ rdrdj(z									ρ2 −1 )= ∫ dj											∫ r(2 - r
Dxy								ρ2 −1								Dxy													0						0
2π																	2π					2r	2			r	4						2

			2
			∫ (2r - r										3	)dr =																													3
= ∫ dj																	∫ dj								-										= 2p (ед									).
= ∫ dj																	∫ dj					2			-	4									= 2p (ед									).
0			0														0					2				4
																															0
																															0
		ПРИМЕР 2.18. С использованием тройного интеграла вычислить объем
тела:
а) заданного в примере 2.10;
б) заданного в примере 2.11.																													x 2 2 4−y2
		Решение. а) V =																							2																2				x 2 2				4−y		2
																																																	4−y		2
																	∫∫∫dxdydz = ∫ dx ∫ dy																			∫ dz =						∫ dx ∫ dy z									=
							(4 - y2 )dy =										V								0				0						0						0				0				0
																	V								0				0						0						0				0				0
2 x 2					2												32
= ∫ dx ∫																	32		;
= ∫ dx ∫																			;
0			0														7				4−x −z
															1		1				4−x −z					1						1
б) V =			∫∫∫dxdydz = ∫ dx ∫ dz																			∫ dy = ∫ dx ∫ dz(y																04−x −z )=
б) V =			∫∫∫dxdydz = ∫ dx ∫ dz																			∫ dy = ∫ dx ∫ dz(y																04−x −z )=
				V											−1		x2					0				−1						x 2

1	1		68
= ∫ dx ∫ (4 - -x - z)dz =				.

-1	x 2	15
	ПРИМЕР	2.19. Вычислить объем тела,				ограниченного поверхностью
(x 2 + y2 + z 2 )2		= xyz.
	Решение. Для вычисления объема перейдем от декартовых к сферическим
координатам:
	x = r × cos j × sin q;				y = r × sin j × sin q; z = r × cos j.
Уравнение поверхности преобразуется к виду
		r4 = r3 × cos j × sin j × sin 2 q × cos q.
Определим пределы изменения для параметров						ϕ, θ, ρ. Так как левая часть

уравнения поверхности всегда положительна, то должна быть положительна и правая часть уравнения, то есть наша поверхность определена в I, III, IV и VIII октантах. Причем, в силу симметрии тела, достаточно вычислить объем в I-м октанте и результат умножить на 4. В первом октанте ϕ, θ, ρ изменяются в

следующих пределах:
	0 £ j £ π ;											0 £ q £ π ;										0 £ r £ cos j × sin j × sin 2 q × cos q.
									2										2
																						p 2			p 2							cos j×sin j×sin				2 q×cos q
V = 4∫∫∫r2 sin qdjdqdr = 4 ∫ dj ∫ sin qdq																																			∫	r2 dr =
					V																		0			0								0
																	3	cos j×sin j×sin 2 q×cos q
																	3	cos j×sin j×sin 2 q×cos q
	p 2					p 2								r																=
= 4 ∫ dj ∫ sin qdq																3														=
		0					0									3
			π 2				π 2											0
	4		π 2				π 2
=	4		∫ dj ∫ sin qdx(cos3 j × sin 3 j × sin 6 q × cos3 q)=
=	3		∫ dj ∫ sin qdx(cos3 j × sin 3 j × sin 6 q × cos3 q)=
	3	0						0												π 2
	4		π 2																	π 2
=			∫		cos3 j × sin 3 jdj ∫ sin 7 q × cos3 qdq =
=	3		∫		cos3 j × sin 3 jdj ∫ sin 7 q × cos3 qdq =
	3	0																	0					π 2
	4		π 2																					π 2
=	4		∫		sin 3 j(1 - sin 2 j)d(sin j) ∫																				sin 7 q × (1 - sin 2 q)d(sin q) =
=	3		∫		sin 3 j(1 - sin 2 j)d(sin j) ∫																				sin 7 q × (1 - sin 2 q)d(sin q) =
	3	0																					0
=	4		π∫2 (sin 3 j - sin 5 j)d(sin j)π∫2 (sin 7 q - sin 9 q)d(sin q) =
=	3
	3	0																					0
	4			sin				4	j			sin			6	j				p 2			sin			8		q			sin	10	q		p 2
								4							6					p 2						8						10			p 2
=										-											×								-							=
=										-											×								-							=
	3						4						6												8						10
	3						4						6												8						10
																				0															0
																				0															0
	4			1			1		1				1						1						3
=						-					-					=							(ед.				).
=	3					-	6				-		10			=			360				(ед.				).
	3		4				6		8				10						360

2.1.9. Приложения тройных интегралов к вычислению массы, центра тяжести и моментов инерции тела

Пусть ϕ(M) - объемная плотность распределения массы в точке

M(x, y, z) тела V, тогда масса тела m, координаты центра тяжести

(x c , yc , z c ) и моменты инерции тела относительно осей 0X, 0Y, 0Z и начала координат 0, вычисляются по формулам

m = ∫∫∫ϕ(M)dv = ∫∫∫ϕ(x, y, z)dxdydz;

(2.19)

x c =

m yz

;

yc =

;

m xy

(2.20)

где m yz ,

m xz ,

m xy - статические моменты тела относительно координатных

плоскостей, вычисляются по формулам

m yz

= ∫∫∫ xϕ(x, y, z)dxdydz;

m xz = ∫∫∫ yϕ(x, y, z)dxdydz ;

m xy

= ∫∫∫ zϕ(x, y, z)dxdydz ;

= ∫∫∫(y2 + z 2 )ϕ(x, y, z)dxdydz ;

I0x

I0 y

= ∫∫∫ (x 2 + z 2 )ϕ(x, y, z)dxdydz ;

(2.21)

I0z

= ∫∫∫(x 2 + y2 )ϕ(x, y, z)dxdydz;

I0 = ∫∫∫(x 2 + y2 + z 2 )ϕ(x, y, z)dxdydz .

(2.22)

Примеры решения задач

x2 + y2 + z2 = R 2

x2 + y2 = Rz

ПРИМЕР 2.20. Найти массу тела, образованного сферической поверхностью x 2 + y2 + z 2 = R 2 и параболоидом вращения

x 2 + y2	= Rz ,
если ϕ(x, y, z) = z	(рис. 2.28).

Решение. По формуле (2.19) m = ∫∫∫ z dxdydz .

x Рис. 2.28


Перейдем к цилиндрическим координатам
		x = r × cos j;		y = r × sin j;				z = z ,
тогда 0 ≤ ϕ ≤ 2π;
	1	(x 2 + y2 )£ z £ +			или	1	r2
	1		R 2 - x 2 - y2			1		£ z £ + R 2 - r2 .
			R 2 - x 2 - y2					£ z £ + R 2 - r2 .
	R					R

Для нахождения пределов изменения ρ необходимо найти линию пересечения

поверхностей

x 2 + y2 + z 2

= R 2

x 2 + y2 = Rz ,

эта

линия

x 2 + y2 =

R 2

(

-1)

цилиндрических

координатах

имеет

вид

R 2

(

-1), т.е.

-1

r2 =

r =

-1 ,

0 £ r £ R

итак

−1

R 2 −ρ2

2π

−ρ

2π

z 2

m = ∫∫∫rz djdrdz =

∫dj

∫rdr

∫z dz =

∫dj

∫rdr

ρ2 R


			R			5	−1																																		R	5	−1
	1	2π	R			2										r		4				1	2π						2	r	2			r	4			r	6		R	2
=	1	∫dj ∫								2	- r		2	-		r						1					R			r			-	r			-	r						=
																		2																						2
	2							R								R		2	rdr =			2	∫dj						2					4				6R		2
	2	0			0											R						2	0						2					4				6R			0
																								2												3					0
		2π			2														4									4
	1	2π			2							5 -1					R		4	5	-1					R		4				5 -1
	1		R						2			5 -1					R			5	-1					R						5 -1
=		∫dj					× R								-										-													=

	2 0			2								2						4 2								6							2

= 5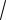5 - 7 R 4 × 2p. 48

z			ПРИМЕР		2.21.	Найти
z			координаты	центра		тяжести
			координаты	центра		тяжести
			пирамиды, образованной плоскостью
1			x + y + z =1	и	координатными
1					ϕ(x, y, z)= y
			плоскостями,	если	ϕ(x, y, z)= y
	z =1 − x − y		(рис. 2.29).
0	1		Решение.	Проекцией плоскости
0		B	y x + y + z =1	на	плоскость X0Y


	y =1 − x		является	треугольник		AOB.
			Координаты	центра		тяжести
			вычисляем по формулам (2.20):
	Рис. 2.29

		1	1−x	1−x−y		1	1−x
m = ∫∫∫ ydxdydz =		∫ dx ∫ y dy ∫ dz = ∫ dx ∫ y dy(1 - x - y) =
	V	0	0	0		0	0		1−x
1	1−x	2	1	y2		xy2		y3
1	1−x	2	1	y2		xy2		y3
= ∫ dx ∫ (y - xy - y			)dy = ∫ dx		-		-		=

0	0		0	2		2		3	0
				2					0

1		(1 - x)3									(1 - x)3													1 1					3									1 (1 - x)4												1				1
1		(1 - x)3									(1 - x)3													1 1					3									1 (1 - x)4												1				1

								-												= -						∫	(1 - x) d(1 - x) = - ×																							= + ;
∫ dx			2					-					3							= -						∫	(1 - x) d(1 - x) = - ×																4							= + ;
0			2										3											6 0														6					4							0				24
			1																					1				1−x	1−x − y									1					1−x							0
																								1				1−x	1−x − y									1					1−x
x c	=					∫∫∫ xy dxdydz = 24∫ x dx ∫ y dy																									∫ dz =				24∫ x dx ∫ y dy(1 - x - y) =
x c	=	1 24				∫∫∫ xy dxdydz = 24∫ x dx ∫ y dy																									∫ dz =				24∫ x dx ∫ y dy(1 - x - y) =
		1 24				V																		0			0				0							0					0
	1					1−x															2						1								y2							y3		1−x
	1					1−x															2						1								y2							y3		1−x
= 24∫ x dx ∫									((1 - x)y - y													)dy = 24∫ x dx								(1 - x)									-									=

	0				0																						0									2						3		0
						(1 - x)										(1 - x)																3										3		0		2							3		4
	1												3									3					1											1
	1													-													1											1

= 24∫ x dx										2										3					= 4∫ x(1 - x )dx = 4∫ (x - 3x + 3x - x )dx =
	0									2										3							0											0
			2			3x		3					3x	4				x		5			1				1
			2					3						4						5			1
	x
= 4				-						+						-									=			;
= 4		2		-	3					+			4			-	5								=			;
		2			3								4				5						0				5
														1									0						1−x 1−x											1−x− y									2
																													1−x 1−x											1−x− y
								yc				=					∫∫∫ y 2 dxdydz =												24 ∫ dx ∫ y 2 dy													∫ dz =									;
								yc				=					∫∫∫ y 2 dxdydz =												24 ∫ dx ∫ y 2 dy													∫ dz =						5			;
													1 24					V											0					0								0						5
																1													1					1−x				1−x − y							1
										zc =						1			∫∫∫ z dxdydz = 24∫ dx ∫ y dy																						∫ dz		=		1		.
										zc =				1 24					∫∫∫ z dxdydz = 24∫ dx ∫ y dy																						∫ dz		=				.
														1 24							V								0					0							0				5
		ПРИМЕР 2.22. Определить момент инерции однородного шара радиуса R
и плотности ϕ(x, y, z) относительно касательной прямой (рис. 2.30).
							z																				Решение. Поместим начало координат в точку
									2R																		касания. Ось 0X направим по касательной, ось
									2R																		0Y будет находится в касательной плоскости,
																											0Y будет находится в касательной плоскости,
																											ось 0Z направим по диаметру шара. И тогда
																											будем		находить								моменты													инерции						I0x .
									R																		Уравнение						сферы относительно																				выбранной
																											Уравнение						сферы относительно																				выбранной
																											системы координат имеет вид
																																				+ (z - R )									2
							0								R							y								x			2	+ y	2										2			- R				2		или
						R																								x				+ y														- R						или

																														z - R ± R 2 - x 2 - y2 .
x						Рис .2.30																						Момент						инерции									I0x							вычислим						по
						Рис .2.30																						Момент						инерции									I0x							вычислим						по

формулам (2.21).

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1710 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.12.2018678.91 Кб2271-88.doc
#
21.09.201980.04 Кб13719664.docx
#
22.12.20183.46 Mб32738_s96.doc
#
17.04.20191.24 Mб6745_f86.doc
#
10.07.2019967.17 Кб77_Экономическая часть_7.doc
#
17.03.20152.11 Mб247УМК.PDF
#
20.07.20191.3 Mб28 деятели.rtf
#
17.03.2015494.92 Кб588 Расчет пространственной модели здания.pdf
#
18.09.201979.36 Кб58 часть.doc
#
19.07.20194.81 Mб48. Дозатор.doc
#
19.11.2018153.09 Кб198. особенности занятий избранным видом спорта.doc