Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

7УМК

.PDF

Скачиваний:

Добавлен:

17.03.2015

Размер:

2.11 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 178 9 10 11 12 13 14 15 16 17 > Следующая >>>

3) Рассмотрим σ3 :			грань ABCD . Уравнение плоскости, в которой лежит
эта грань есть x = 0 , тогда dx = 0 . Подставим эти данные в (*):
	Iσ3	=	∫∫ 0 dydz + y 0 dz + z 0 dy = 0 .
			ABCD
4) Рассмотрим σ4 : грань D1DCC1 . Уравнение плоскости, в которой лежит
эта грань есть z = 1, тогда dz = 0. Подставим эти данные в (*):
Iσ4	=	∫∫ xdy 0 + y dx 0 + 1 dxdy = ∫∫ dxdy =
	D1DCC1					D1DCC1
1	1		1	1
= ∫ dx∫ dy = ∫ dx(y					10 )= ∫ dx = x	10 = 1.


0	0		0	0

5) Рассмотрим σ5 :

грань B1C1CB. Уравнение плоскости, в которой лежит

эта грань есть y = 1, тогда dy = 0 . Подставим эти данные в (*):

Iσ5 =

∫∫ x 0 dz + 1 dxdz + z dx 0 =

∫∫ dxdz = ∫ dx∫ dz = 1.

B1C1CB

6) Рассмотрим σ6 :

грань

A1D1C1B1 . Уравнение плоскости, в которой

лежит эта грань есть x = 1, тогда dx = 0 . Подставим эти данные в (*):

Iσ6 =

∫∫1 dydz + y 0 dz + z 0 dy =

∫∫ dydz = ∫ dy∫ dz = 1.

A1D1C1 B1

A1D1C1B1

0 0

Ответ: I = Iσ

+ Iσ

= 0 + 0 + 0 +1 +1 +1 = 3.

Замечание (к

примеру).

Эту

же

задачу

можно

решить значительно

быстрее, если применить формулу Остроградского – Гаусса (1.93). Так как по

условию	X(x, y, z) = x ,	Y(x, y, z) = y ,			Z(x, y, z) = z , то	∂X(x, y, z) = 1,
∂Y(x, y, z) = 1, ∂Z(x, y, z) = 1.						∂x
∂Y(x, y, z) = 1, ∂Z(x, y, z) = 1.
∂y	∂z
По формуле 1.93:
	I = ∫∫ xdydz + ydxdz + zdxdy = ∫∫∫ (1 + 1 + 1)dxdydz =
	σ				V
		1	1	1
	= 3∫∫∫ dxdydz = 3∫ dx∫ dy∫ dz				= 3.
	V	0	0	0

УЧЕБНО - МЕТОДИЧЕСКИЙ КОМПЛЕКС

РАЗДЕЛ 7 «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ»

2. Методические указания для студентов

ВВЕДЕНИЕ

Кратные (двойные, тройные), криволинейные и поверхностные интегралы, как и обыкновенные (однократные) определенные интегралы, служат для вычисления различных величин.

Суть общего метода вычисления этих величин заключается в следующем.

1.Искомая величина разбивается на большое число малых элементов.

2.Вычисляется приближенное значение (главная часть) каждого элемента

ипутем их суммирования находится приближенное значение всей искомой величины в виде интегральной суммы.

3.Находится предел этой интегральной суммы, который дает точное значение искомой величины.

В задачах, решаемых с помощью кратных, криволинейных или поверхностных интегралов, вычисление величины сводится к вычислению предела интегральной суммы, распространяющейся или на плоскую область измерения двух переменных, или на пространственную область измерения трех переменных, или вдоль дуги некоторой кривой, или по некоторой поверхности, который и называется соответственно двойным, тройным, криволинейным и поверхностным интегралом.

2.1.КРАТНЫЕ ИНТЕГРАЛЫ

Если функция f (М) непрерывна в некоторой замкнутой области D Ì R 2 и если разбить эту область произвольным способом на n частичных областей с площадями S1 , S2 ,..., Sn , выбрать в каждой из них по одной произвольной точке M1 , M 2 ,..., M n , вычислить значение функции в этих точках и составить сумму

f (M

)× DS + f (M

)× DS

+ ... + f (M

)× DS

= ∑n

f (M

)× DS

, (2.1)

i=1

то она называется интегральной суммой функции f (M) по плоской области

Если функция f (M) непрерывна в некоторой замкнутой пространственной области V Ì R 3 и если разбить эту область произвольным способом на n частичных областей с объемами V1 , V2 ,..., Vn , выбрать в каждой из них по одной произвольной точке M1 , M 2 ,..., M n , вычислить значения функции в этих точках и составить сумму

f (M	)× DV + f (M	2	)× DV + ... + f (M	n	)× DV	= ∑n	f (M	)× DV , (2.2)
1	1	2	2	n	n	i=1	i	i
						i=1

то она называется интегральной суммой функции f (M) по пространственной области V.

Интегральная сумма зависит как от способа разбиения исходной области на n частичных областей, так и от выбора в них точек M1 , т.е. для всякой непрерывной функции f (M) и всякой замкнутой области, где эта функция определена и непрерывна, можно составить бесконечное множество интегральных сумм. Но при неограниченном увеличении n и при стремлении к нулю наибольшей из частичных подобластей все эти интегральные суммы

имеют один общий предел.

ОПРЕДЕЛЕНИЕ. Предел интегральной суммы (2.1) называется

двойным интегралом и обозначается ∫∫ f (M)ds .

ОПРЕДЕЛЕНИЕ. Предел интегральной суммы (2.2) называется

тройным интегралом и обозначается ∫∫∫f (M)dv .

Двойной и тройной интегралы обладают всеми основными свойствами обыкновенного определенного интеграла:

1.Постоянный множитель можно выносить за знак интеграла.

2.Интеграл от суммы функций равен сумме интегралов.

3.Область интегрирования можно разбивать на части.

Вычисление двойного и тройного интегралов сводится к вычислению соответственно двукратного и трехкратного интегралов, к оптимальной расстановке пределов интегрирования. Причем значение интеграла не зависит от порядка интегрирования.

Замечание 1. Пределы внешнего интеграла всегда есть постоянные величины (числа).

Замечание 2. Начинаем интегрирование с внутреннего интеграла.

2.1.1. Вычисление двойного интеграла в декартовой системе координат

Если область интегрирования D отнесена к прямоугольной системе координат X0Y и если она разбивается на частичные области сетью прямых,

параллельных осям координат	(рис.2.1), то площадь частичной	области
ds = dx × dy (как площадь прямоугольника со сторонами dx и dy) и
∫∫ f (M)ds = ∫∫ f (x, y)dxdy .		(2.3)
D	D

Случай 1. Если область D правильная вдоль оси 0Y, т.е. такова, что любая прямая, проходящая внутри области D параллельно оси 0Y, пересекает ее границу в двух точках (рис. 2.1), то в этом случае область определяется неравенствами вида ϕ1 (x) ≤ y ≤ ϕ2 (x), a £ x £ b , тогда пределы интегрирования расставим таким образом:

	b	ϕ2 (x )	b	ϕ2 (x )
∫∫ f (x, y)dxdy = ∫ dx					(2.4)
∫∫ f (x, y)dxdy = ∫ dx		∫ f (x, y)dy = ∫		∫ f (x, y)dy dx .	(2.4)
D	a	ϕ1 (x )	a	ϕ1 (x )

y = ϕ2 (x)

y = ϕ1 (x)

0 a	dx	b	x

Рис. 2.1

Случай 2. Если область D правильная вдоль оси 0X (т.е. такова, что любая прямая, проходящая внутри области D параллельно оси 0X, пересекает границу этой области в двух точках, а любая прямая, например, AB рис.2.2, проходящая внутри области D параллельно оси 0Y, пересекает границу этой области более, чем в двух точках), то в этом случае область можно определить

неравенствами вида	ψ1 (y) ≤ x ≤ ψ 2 (y);			c ≤ y ≤ d .	Тогда	пределы
интегрирования расставим таким образом:
	d	ψ2 (y )	d	ψ2 (y )
∫∫ f (x, y)dxdy = ∫ dy						(2.5)
∫∫ f (x, y)dxdy = ∫ dy		∫ f (x, y)dx = ∫		∫ f (x, y)dx dy .		(2.5)
D	c	ψ1 (y )	c	ψ1 (y )
y
D		B
D	x = ψ1 (x)
	x = ψ1 (x)			x = ψ2 (x)
				x = ψ2 (x)
C		A
0		A		x
				x

		Рис. 2.2

Примеры решения задач

				ПРИМЕР 2.1. Вычислить																												∫∫ (x 2 - y)dxdy и
					y																							а)				∫∫ (x 2 - y)dxdy и
																																D	∫∫ (x + 2)3 × (y +1)2 dxdy ,
					1																							б)					∫∫ (x + 2)3 × (y +1)2 dxdy ,																						где				область
																																	D
																												интегрирования																	D										определяется
				− 1																						x		неравенствами: −1 ≤ x ≤ 2																									и					0 ≤ y ≤ 1
				− 1		0						1					2									x		(рис. 2.3).
						0						1					2											(рис. 2.3).
					Рис. 2.3
												∫∫ (x 2 - y)dxdy =																	2				1					- y)dy =
				Решение. а)								∫∫ (x 2 - y)dxdy =																	∫ dx∫ (x 2									- y)dy =
												D																	−1				0
	2			1							1										2							1					1									2										y2					1


=		∫ dx ∫ x 2 dy -									∫ ydy						=					∫ dx x 2						∫ dy					- ∫ ydy =									∫ x 2 dx y							10	-									=
=		∫ dx ∫ x 2 dy -									∫ ydy						=					∫ dx x 2						∫ dy					- ∫ ydy =									∫ x 2 dx y							10	-									=
	−1			0							0										−1							0					0									−1												2
	−1			0							0										−1							0					0									−1												2
																																																									0
	2			2			1						1 2					2								1 x 3						2			1					23				(-1)3							1 8							1		3
	2			2			1						1 2					2								1 x 3						2			1					23				(-1)3							1 8							1		3

= ∫ x dx 1 -											=					∫ x dx = ×																	= ×									-						=								+				= ;
= ∫ x dx 1 -											=		2			∫ x dx = ×																	= ×							3		-		3				=						3		+				= ;
	−1						2						2			−1														2 3		−1			2					3				3							2			3				3		2
	−1															−1														2 3		−1
б) ∫∫ (x + 2)3 × (y +1)2 dxdy = ∫2 (x + 2)3 dx																																		1∫ (y +1)2 dy =
		D																							−1									0								(y +1)3					1
=	2				3			1			(y +1)						2											=			2						3													=
	2				3			1									2														2						3
		∫ (x + 2) dx ∫																	d(y +1)												∫ (x +				2)				dx
	−1							0																					−1															3
	−1							0																					−1															3			0
	2											3			3								7		2												7			2							0
	2											3			3										2															2
=		∫ (x + 2)3 dx								2			-		1					=					∫	(x + 2)3 dx =														∫ (x + 2)3 d(x + 2) =
=		∫ (x + 2)3 dx											-							=					∫	(x + 2)3 dx =														∫ (x + 2)3 d(x + 2) =
	−1			(x +	2)			3								3					3				−1												3			−1
	7					4		2					7						4						4				7							1					7			255				7 ×85
						4		2											4						4
																4								1
=			×								=				×							-					=				64 -									=			×		=									.
=	3		×	4							=				×		4					-			4		=		3		64 -					4				=			×		=					4				.
	3			4				−1						3			4								4				3							4					3 4									4
								−1						3																										быстрее,
				Данный					интеграл													можно						вычислить												быстрее,						поскольку													пределы

интегрирования у внутреннего и внешнего интеграла являются постоянными

величинами	и подынтегральная				функция			f (x, y)			представлена			в виде
f (x, y) = f1 (x)× f 2 (y).												(x + 2)4	2
3	(y +1)	2	dxdy =	2	3	1	(y +1)		2					´
3		2		2	3	1			2
∫∫ (x + 2) ×				∫ (x + 2)		dx × ∫				dy =		4
D				−1		0						4
D				−1		0							−1
													−1

(y +1)3					1						(2 + 2)4								(-1 + 2)4										(1 +1)3												(0 +1)3
(y +1)3					1						(2 + 2)4								(-1 + 2)4										(1 +1)3												(0 +1)3
´						=												-												×									-														=
´		3				=								4				-						4						×				3					-						3								=
		3												4										4										3											3
					0																																								1	8							1			255		7		7 ×85
					0
	y
																																		=			64 -													-					=		×		=
																																		=			64 -								4					-			3		=	4	×	3	=	4
																																													4	3							3			4		3		4
																																		.
1																																		ПРИМЕР 2.2. Вычислить
1																				y = x																									∫∫ (x 2 - y)dxdy ,
																				y = x																									∫∫ (x 2 - y)dxdy ,
																																													D
																																			где				область											интегрирования									D
																																		определяется																					неравенствами
																																		(рис. 2.4):
																				y = 1 − x																				x + y £ 1;
																				y = 1 − x																					y ³ x;
																																									y ³ x;
		0							0,5									1														x								x ³ 0.
										Рис. 2.4
Решение. ∫∫ (x							2		- y)dxdy									=	0,5					1−x				2									0,5						1−x						2	dy -
Решение. ∫∫ (x									- y)dxdy									=			∫ dx ∫					(x			- y)dy =									∫ dx								∫ x				dy -
					D														0						x													0								x
1−x				0,5									2	1−x				1−x										0,5						2			1		x					y2			1−x
				0,5																								0,5

																																					−
- ∫ ydy			= ∫ dx x												∫ dy - ∫ ydy											= ∫ dx							x		y		x			-													=
- ∫ ydy			= ∫ dx x												∫ dy - ∫ ydy											= ∫ dx							x		y		x			-					2								=
	x			0											x				x									0																	2
																(1 - x)2									x 2																						x
																																															x
0,5			2	(1 - x - x) -																										0,5						2						3									1
																													= ∫
																						+											x - 2x + x -																					dx =
= ∫ dx x																		2				+			2								x - 2x + x -																					dx =
0																		2							2					0																					2
	x 3	0,5				x 4		0,5							x 2		0,5				1			0,5					1
		0,5						0,5									0,5							0,5
=		- 2										+						-					x				=				.
=		- 2										+						-					x				=				.
3		0		4				0						2			0		2					0					96
		0						0									0							0	∫∫ (x + y)dxdy ,
		ПРИМЕР							2.3.						Вычислить										∫∫ (x + y)dxdy ,														где область																D	ограничена
																									D
прямыми линиями y = 1, y = 3, x = 0 , x = 2y (рис. 2.5).
		Решение. а) ∫∫ (x + y)dxdy =																							3				2 y												3							2 y
		Решение. а) ∫∫ (x + y)dxdy =																							∫ dy ∫					(x + y)dx = ∫ dy																			∫ xdx +
											D														1				0	(2y)											1								0
	2 y			3				x				2			2 y							2 y					3									2																3
	2 y			3								2			2 y												3									2																3

+ y ∫ dx			= ∫ dy													+ y × x									=		∫ dy										+ y × 2y											=		4∫ y2 dy =
+ y ∫ dx			= ∫ dy													+ y × x									=		∫ dy										+ y × 2y											=		4∫ y2 dy =
0				1							2											0					1						2																			1
0				1							2											0					1						2																			1
														0

	y	3	3		3	3		1		104


= 4				= 4			-		=		;
					3			3		3
3			1

y = x 2

2 D1 D2

б) если внешний интеграл вычислить по переменной x, то придется область интегрирования разбить на две подобласти, в связи с чем и двойной интеграл будет представлен суммой двух двойных интегралов:

∫∫ (x + y)dxdy =

Рис. 2.5

		2	3	6	3	(x + y)dy =
= ∫∫ (x + y)dxdy + ∫∫ (x + y)dxdy = ∫ dx∫				(x + y)dy + ∫ dx ∫		(x + y)dy =
D1	D2	0	1	2	x 2

2		3						3								6			3				3								2						y		2		3
																																			3		y
= ∫ dx		∫ xdy + ∫ ydy +																										=								+							+
																∫ dx					∫ xdy + ∫ ydy							=			∫ dx x y				1	+	2						+
																∫ dx					∫ xdy + ∫ ydy										∫ dx x y				1
0		1						1								2			x 2				x 2								0											1
																			x 2																							1
6						3			y		2		3						2					9			1					6						x		2			9		x	2
6											2		3						2													6								2						2

								+									=						- x +			-								3x		-					+			-			=
= ∫ dx x y					x 2			+									=		∫ dx 3x				- x +			-					+ ∫ dx			3x		-					+			-			=
= ∫ dx x y					x 2														∫ dx 3x					2 2							+ ∫ dx						2						2 8
2										2			x 2						0					2 2								2					2						2 8
										2			x 2																2
2	(2x	+ 4)dx +								6				5			2					9			2x 2				2				2
= ∫										∫				5			2					9			2x 2								2
											-				x				+ 3x +				dx =								+ 4x		0	+
											-				x				+ 3x +				dx =								+ 4x			+
														8								2				2
0										2				8								2				2				0
				3						2								6
																		6
- 5			x					3x						9x						104
- 5			x					3x						9x						104
+		×					+					+							=			.
+	8	×	3				+	2				+		2					=	3		.
	8		3					2						2				2		3
																		2

Последний пример подтверждает, что порядок интегрирования не влияет на значение интеграла. Поэтому для экономии вычислительной работы следует, если это возможно, выбирать такой порядок интегрирования, при котором нет надобности разбивать область интегрирования на части.

ПРИМЕР 2.4. Изменить порядок интегрирования в двукратном интеграле:

1	1+ 1−y		2	0	x		(x, y)dy ;	2	4
а) ∫ dy		∫ f (x, y)dx ;		б) ∫ dx ∫ f				в) ∫ dx ∫ f (x, y)dy .
0		y		−1	−			−2	x 2
						−x

Решение. а) область интегрирования представлена на рис. 2.6. Эта область

ограничена прямой линией			y = x	и окружностью		(x − 1)2 + y2 = 1, причем
0 ≤ y ≤ 1.
	1+
1	1+	1−y2	1	x	2		1−(x−1)2
∫ dy ∫ f (x, y)dx = ∫ dx∫ f (x, y)dy + ∫ dx							∫ f (x, y)dy;
0		y	0	0	1	0

б) область интегрирования (рис. 2.7) ограничена прямой линией y = x и

ветвью параболы y = −

или y2

= −x (x ≤ 0), причем − 1 ≤ x ≤ 0 .

− x

− y2

∫ dx ∫ f

(x, y)dy = ∫ dy ∫ f (x, y)dx ;

−1

−

−1

−x

y = x

− 1

y2 = −x

− 1

y = x

Рис. 2.6

Рис. 2.7

в) область интегрирования (рис. 2.8) ограничена прямой линией y = 4 и

параболой y = x 2 .

y = x 2

∫ dx ∫ f (x, y)dy =

∫ dy ∫ f (x, y)dx

−2

x 2

−

− 2 − 1

Рис. 2.8

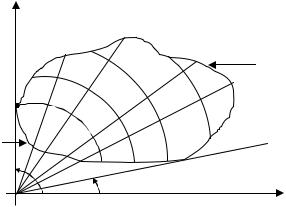
2.1.2. Вычисление двойного интеграла в полярной системе координат

Если область интегрирования двойного интеграла задана в полярных координатах j и ρ = ρ(ϕ) и если она разбивается на частичные подобласти лучами ϕ = const , исходящими из точки О (называемой полюсом), и

концентрическими окружностями ρ = const с центром в полюсе (рис. 2.9), то ds = r × djdr и

∫∫ f (M)ds = ∫∫ f (ϕ, ρ)ρdϕdρ.	(2.6)
D

ρ = ρ2 (x)

ρ = ρ1 (x)

ϕ2

ϕ1

Рис. 2.9

Поскольку

формулы связи декартовых и

полярных координат:

x = r × cos j;

y = r × sin j, то множитель r в правой части формулы (2.6) есть

r =

, где J –

это определитель второго порядка, называемый якобианом:

x'ρ

x'ϕ

cos j

- rsin j

r × cos2

j + r × sin 2 j

= r.

y'ρ

y'ϕ

sin j

rcos j

Обычно двойной интеграл в полярных координатах выражается через двукратный интеграл вида

	ϕ2	ρ2
∫∫ f (j, r)rdjdr = ∫ dj ∫ f (j, r)rdr.			(2.7)
D	ϕ1	ρ1

Примеры решения задач

ПРИМЕР 2.5. Преобразовать к полярным координатам и затем вычислить

двойной интеграл, заданный в декартовых координатах ∫∫	ln(x	2 + y2 )
			dxdy ,
	x 2	+ y2
D

<<< < Предыдущая 1 2 3 4 5 6 78 / 178 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.12.2018678.91 Кб2271-88.doc
#
21.09.201980.04 Кб13719664.docx
#
22.12.20183.46 Mб32738_s96.doc
#
17.04.20191.24 Mб6745_f86.doc
#
10.07.2019967.17 Кб77_Экономическая часть_7.doc
#
17.03.20152.11 Mб247УМК.PDF
#
20.07.20191.3 Mб28 деятели.rtf
#
17.03.2015494.92 Кб588 Расчет пространственной модели здания.pdf
#
18.09.201979.36 Кб58 часть.doc
#
19.07.20194.81 Mб48. Дозатор.doc
#
19.11.2018153.09 Кб198. особенности занятий избранным видом спорта.doc