Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Нефтяной Технический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

7УМК

.PDF

Скачиваний:

Добавлен:

17.03.2015

Размер:

2 Мб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1713 14 15 16 17 > Следующая >>>

I xoy	= ∫∫ z 2 F(x, y, z)ds ;			I xoz	= ∫∫ y2 F(x, y, z)ds ;
	σ				σ
	I yoz	= ∫∫ x 2 F(x, y, z)ds .				(2.55)
		σ
Моменты инерции Iox ,		Ioy ,	Ioz относительно координатных осей и
начала координат вычисляем по формулам:
Iox = ∫∫ (y2 + z 2 ) F(x, y, z)ds ;			Ioz = ∫∫ (x 2 + y2 ) F(x, y, z)ds ;
σ				σ
Ioy = ∫∫ (x 2 + z 2 ) F(x, y, z)ds ;			Io = ∫∫ (x 2 + y2 + z 2 ) F(x, y, z)ds . (2.56)
σ				σ
	Примеры решения задач
ПРИМЕР	2.39. Найти		площадь		части поверхности	z 2 = 2xy ,
расположенной в первом октанте между плоскостями x = 2 и						y = 4 (рис.
2.36).

4 y

Рис. 2.36

Решение. Применяя формулы (2.48) и (2.51), получаем

(здесь F(M) = F(x, y, z) ≡ 1)

dxdy

S = ∫∫ ds =

∫∫

1 + (z′x )2 + (z′y )2

= (

)′x =

Dxy

= (

)′y =

z′

, D

2xy

- прямоугольник

2xy

0 ≤ x ≤ 2 , 0 ≤ y ≤ 4. Итак

	2	4					y		2				x	2					2		4	x			+ y							1				2					4			x						y
∫ dx∫				1 +			y				+		x			dy =			∫ dx∫			x			+ y					dy =		1				∫ dx∫								x	+					y		dy =
						2xy							2xy
																								2xy								2																		x
	0	0																	0		0			2xy								2				0						0		y						x
																																								1		4									3		4
																																								1		4									3		4
	1	2		4			1					1				1				1						1			2			1					y							−		1		y
							1				−	1				1		−		1												1								2						1					2
											−							−																						2											2
=			∫ dx∫		x 2				y			2 + y 2 x								2 dy		=								∫ dx x 2													+ x 2											= 1
=			∫ dx∫		x 2				y			2 + y 2 x								2 dy		=								∫ dx x 2													+ x 2											= 1
	2	0																									2		0										1										3
	2	0		0																							2		0										1										3
																																				2											2
																																										0											0
																																										0											0
																											3	2							1			2
																											3	2							1			2
	1	2			1					16					1				1				x								16		x
																											2								2
														−
														−
=			∫ dx		4x 2 +								x		2 =						4								+												=
=			∫ dx		4x 2 +								x		2 =						4								+												=
	2	0									3								2						3				3					1
	2	0									3								2						3				3					1
																						2										2
	1		16					16																				0										0
																												0										0

=					2 +												= 16 (кв. ед.).
											2 2
									3		2 2
	2		3						3

ПРИМЕР 2.40. Найти массу полусферы, если в каждой ее точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы.

Решение. Поместим начало прямоугольной системы координат в центр основания полусферы и направим ось аппликат перпендикулярно этому

основанию. Тогда уравнение полусферы будет z = +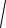R 2 − x 2 − y2 , R -

радиус полусферы. Поверхностная плотность в точке M(x, y, z) полусферы:

F(x, y, z) =

x 2 + y2 . Воспользуемся формулой (2.48) и (2.52), где D xy есть

круг x 2 + y2

= R 2 :

m = ∫∫ F(x, y, z)ds = ∫∫

dxdy =

x 2 + y2

1 + (z′x )2 + (z′y )2

Dxy

− x

− y

= ∫∫ x 2 + y2

1 +

dxdy =

Dxy

− x

− y

− x

− y

= R ∫∫

x 2 + y2

dxdy = (перейдем к полярным координатам)=

Dxy

R 2 − (x 2 + y2 )

dρ

cos

ϕ + ρ

sin

2π

= R ∫∫

ρdϕdρ = R ∫ dϕ∫

R 2 − (ρ2 cos2

R 2 − ρ2

Dxy

ϕ + ρ2 sin 2 ϕ)

π2 R 3

можно

вычислить

с помощью замены:

(внутренний интеграл

ρ2

= R sin t).

ПРИМЕР 2.41. Найти центр тяжести однородной поверхности

параболоида y2 + z 2

= 10x , отсеченной плоскостью x = 10

(рис. 2.37).

Решение.

Данная однородная

поверхность

симметрична

относительно оси OX, поэтому yc

= 0 ,

zc = 0. Необходимо вычислить x c , для

этого

вычислим

статический

момент

M yoz

и массу m поверхности

по

формулам (2.51) и (2.53). Поверхность σ

проектируется

на

координатную

плоскость YOZ.

Проекцией

D yz

является

круг

M yoz

y2 + z 2

= 100 .

Так

как поверхность

Рис. 2.37

однородная, то полагаем F(x, y, z) ≡ 1.

= ∫∫ x F(x, y, z)ds =

+ z 2

∫∫

1 +

dydz =

Dyz

=	1			∫∫ (y2 + z 2 )						25 + (y2 + z 2 ) dydz =												(перейдем		к	полярным
=				∫∫ (y2 + z 2 )						25 + (y2 + z 2 ) dydz =												(перейдем		к	полярным
	50 Dyz
								1		∫∫ ρ2					ρdϕdρ =
координатам)							=	1			25 + ρ2
координатам)							=				25 + ρ2
								50 Dyz
	1			2π	10									50		π(1 + 25						).
				2π	10		25 + ρ2 ρdρ =
=				∫ dϕ ∫ ρ2															5
=				∫ dϕ ∫ ρ2										3					5
50				0	0									3
						1			25 + (y2 + z 2 ) dydz =								1	∫∫					ρdϕdρ =
m = ∫∫ ds =						1	∫∫										1					25 + ρ2
m = ∫∫ ds =							∫∫															25 + ρ2
				σ		5 Dyz											5 Dyz
		2π			10								2π	10					1
		2π			10								2π	10					1
=	1		∫ dϕ ∫ 25 + ρ2 ρdρ =									1	∫ dϕ ∫ (25 + ρ2 )								d(25 + ρ2 )=
	1											1								2
																				2
5			0		0				10				0	0

							10
							10
		2π		2		3
						3
	1		(25 + ρ		)2				50	π(5		)−1.
=	1	∫ dϕ	(25 + ρ		)2			=	50		5
=		∫ dϕ						=			5
10		0	3					3

			2
							0
							0

M yoz

Итак, окончательно по формуле (2.54) получаем x c

5 −1

ПРИМЕР 2.42. Найти момент инерции однородной

полусферы

z = + a 2 − x 2 − y2	относительно оси OZ.
Решение. По формулам (2.56) и учитывая, что поверхность σ -
однородная, т.е. F(x, y, z) ≡ 1 (кроме				того, поверхность проектируется на
плоскость XOY), получается:
Ioz = ∫∫ (x 2 + y2 )ds =
σ

= ∫∫ (x 2 + y2 ) 1 +	x 2	+		y2	dxdy =
= ∫∫ (x 2 + y2 ) 1 +	a 2 − x 2 − y2	+	a 2	− x 2 − y2	dxdy =
Dxy	a 2 − x 2 − y2		a 2	− x 2 − y2

Z –

∫∫

x 2 + y2

dxdy = a ∫∫

ρ2 cos2 ϕ + ρ2 sin 2 ϕ

ρdϕdρ =

a 2

Dxy

− (x 2 + y2 )

Dxy

a 2 − (ρ2 cos2 ϕ + ρ2 sin 2 ϕ)

2π

π a 4 .

∫ dϕ∫

dρ =

a 2 − ρ2

2.3.3. Поверхностные интегралы второго рода или по координатам, их вычисление

Поверхностные интегралы второго рода по координатам X и Y, Y и Z, X и

это интегралы вида
∫∫ F(x, y, z)dxdy ,	∫∫ F(x, y, z)dydz ,	∫∫ F(x, y, z)dxdz (2.57)
σ	σ	σ

или в общем виде
∫∫ F(x, y, z)dxdy + Q(x, y, z)dydz + R(x, y, z)dxdz .	(2.58)
σ

Вычисление этих интегралов также сводится к вычислению двойных интегралов: исходя из уравнения поверхности σ, подынтегральное выражение преобразуется к двум переменным, область изменения которых есть проекция поверхности σ на соответствующую координатную плоскость.

Например, для первого интеграла из формулы (2.57):

если область интегрирования поверхностного интеграла ∫∫F(x, y, z)dxdy , т.е.

поверхность σ имеет уравнение	σ
поверхность σ имеет уравнение	z = z(x, y), то данный интеграл вычисляем
так:
∫∫F(x, y, z)dxdy = ± ∫∫F(x, y, z(x, y))dxdy ,		(2.59)
σ	σxy

где двойной знак соответствует двум различным сторонам поверхности σ : где знак «плюс» соответствует интегрированию по той стороне поверхности σ , которая обращена в сторону положительного направления оси OZ.

Замечание. Поверхностный интеграл по координатам x , y , взятый по куску цилиндрической поверхности с образующими, параллельными оси OZ, равен нулю.

Аналогичная теория и для двух других интегралов из формулы (2.57). Для интеграла (2.58) ниже приведем формулы Стокса и Остроградского-

Гаусса.

Формула Стокса: Если поверхность σ - незамкнута и ограничена контуром l , то имеет место формула

∫F(x, y, z)dx + Q(x, y, z)dy + R(x, y, z)dz =

l
= ∫∫(R′y − Q′z )dydz + (Fz′ − R′x )dxdz + (Q′x − Fy′ )dxdy .	(2.60)
σ

Частный случай формулы Стокса (формула Грина) изложен в 1-й главе.

Формула Остроградского-Гаусса. Если поверхность σ - замкнутая, V –

тело, которое ограничивается поверхностью σ. Тогда имеет место формула ∫∫F(x, y, z)dydz + Q(x, y, z)dxdz + R(x, y, z)dxdy = ∫∫∫(Fx′ + Q′y + R′z )dxdydz,

+σ	V
	(2.61)
где функции	F(x, y, z), Q(x, y, z), R(x, y, z) и их частные производные

должны быть непрерывными в области V.

Применения поверхностных интегралов второго рода к вычислению физических величин в данный практикум не вошли, так как представляют собой достаточно объемный материал из теории поля.

Примеры решения задач

ПРИМЕР 2.43. Вычислить поверхностный интеграл второго рода (по координатам)

I = ∫∫2dxdy + ydxdz − x 2 zdydz ,

где σ - внешняя сторона части эллипсоида

4x 2 + y2 + 4z 2 = 4 ,

расположенной в первом октанте (рис. 2.38).

C(0;0;1)

								y2 + 4z2 = 4




								B(0;2;0)

0
								y

A(1;0;0)

4x2 + y2 = 4

Рис. 2.38

Решение. Расчленяем данный поверхностный интеграл по координатам общего вида на три слагаемых интеграла:

I = 2 ∫∫ dxdy + ∫∫ y dxdz − ∫∫ x 2 z dydz

σ σ σ

и, пользуясь уравнением поверхности σ и формулой (2.59), преобразуем каждый из них в двойной интеграл:

I1 = ∫∫ dxdy = ∫∫ dxdy , где σxy - проекция поверхности σ на плоскость

σσxy

XOY, т.е. часть AOB эллипса 4x 2 + y2 ≤ 4 ;

I2 = ∫∫ y dxdz = ∫∫ y dxdz =
I2 = ∫∫ y dxdz = ∫∫ y dxdz =		y =	1 − x 2 − z 2	= 2 ∫∫ 1 − x 2 − z 2 dxdz ,
σ	σxz			σxz
σ	σxz			σxz

где σxz - проекция поверхности σ на плоскость XOZ, т.е. часть OAC круга

4x 2 + 4y2

≤ 4.

(4 − y2 − 4z 2 ) z dydz,

I3 = ∫∫ x 2 z dydz = ∫∫

σyz

где σyz - часть OBC эллипса y2 + 4z 2

≤ 4 .

x = cos t

4−4x 2

− x 2 dx

Итак: I1 = ∫∫ dxdy = ∫ dx

∫ dy = 2∫ 1

dx = −sin t dt

σxy

= −2∫ sin 2

t dt = 2

∫ 1 − cos 2tdt = ∫ (1 − cos 2t)dt = ∫ dt − ∫ cos 2tdt =

		π					1								π	= π ;
= t		π		−					sin 2t						2
		2


		0				2									0						2			dxdz =								x = ρcos ϕ																														ρdϕdρ =
		0




I2	= 2 ∫∫										1 − x 2 − z 2																																			= 2 ∫∫ 1 − ρ2
				σxz																												z = ρsin ϕ																	σxz
		π		σxz																												1			π														σxz
		π																																	π
		2				1																													2					1									1 2
						1									2																									1							2												2
															2																																2												2
=	2∫ dϕ∫										1 − ρ					ρdρ = 2													−						∫ dϕ∫							(1 − ρ							)		d(1					− ρ					) =
=	2∫ dϕ∫										1 − ρ					ρdρ = 2													−						∫ dϕ∫							(1 − ρ							)		d(1					− ρ					) =
		0				0											1															2			0					0
	π																									π																				π											π
	π																									π																				π
														3 2
	2					(1				− ρ2 )													2													2							2			2						2					2							π
	2					(1				− ρ2 )													2													2							2			2						2					2							π
=	∫ dϕ																						= −∫ dϕ										0 −							=						∫ dϕ =									ϕ		0		=			;
	0											3											0													3							3			0						3										3

												2
																		0
																		0
												y	2						2																1								4−4z2											2				y			2
				∫∫								y							2				z dydz = ∫ zdz																						∫									2				y
I3	=									−					− z																																			− z						−
I3	=					1				−		4			− z																																	1		− z						−			4				dy =
				σyz								4																							0								0																4
																															2
								(1 − z 2 )y								0										− y					2			1−z2
= ∫ zdz								(1 − z 2 )y								0										− y			3										=
	1															2				1−z2									3
	0																						12							0
	0


= 1∫ (1 − z 2 ) 2																							−			8		(1 − z 2 )3 2 zdz =
														1 − z 2												8
														1 − z 2
	0																						12
= 1∫ (2 (1 − z 2 )3 2 −																			2			(1 − z 2 )3 2											zdz =									4		1∫ (1 − z 2 )3 2 zdz =
= 1∫ (2 (1 − z 2 )3 2 −																						(1 − z 2 )3 2											zdz =											1∫ (1 − z 2 )3 2 zdz =
	0																		3																							3 0
	4							1													3 2																												5 2		1
																																																			1

												1						2												2									2 (1 − z 2 )
=			−									∫ (1			− z						)			d(1 − z									) = −																			=
=	3		−					2				∫ (1			− z						)			d(1 − z									) = −					3								5						=
	3							2				0																										3								5
= −			4		(1 − z 2 )5 2											1 = −									4		(0 −1) =										4				.					2					0
																																														2					0



		15														0							15													15
		15														0							15													15
				Итак: I = 2 I1 + I2 − I3 = 2 π + π −																																											4			=			4		π −					4				.
				Итак: I = 2 I1 + I2 − I3 = 2 π + π −																																														=					π −									.
																																						2					3			15						3							15

ПРИМЕР 2.44. Вычислить поверхностный интеграл второго рода (по координатам)

I = ∫∫ 4x 3dydz + 4y3dxdz − 6z 4 dxdy ,

+σ

где σ - полная поверхность цилиндра x 2 + y2 = a 2 , 0 ≥ z ≤ h (рис. 2.39).

C(− a;0; h)

z = h

x2 + y2 = a 2

A(a;0;0)

Рис. 2.39

Решение. Воспользуемся формулой Остроградского-Гаусса (2.61):

I = ∫∫ 4x 3dydz + 4y3dxdz − 6z 4 dxdy = ∫∫∫ (12x 2 +12y2 − 24z3 )dxdydz =

+σ

= 12 ∫∫∫ (x 2 + y2 − 2z3 )dxdydz = 12

∫∫ dxdyh∫ (x 2 + y2 − 2z3 )dz =

x 2 +y2 ≤a

= 12

(x 2 + y2 ) z −

∫∫ dxdy

x2 +y2 ≤a

(x 2 + y2 ) h −

= 12

∫∫ dxdy

dxdy =

x2 +y2 ≤a

= 12 h

∫∫ (x 2 + y 2 )dxdy − 6 h 4

∫∫ dxdy = 12 h I1 − 6 h 4 I2 .

x 2 +y2 ≤a

Вычисляем отдельно интегралы I1 ,

I2 :

∫∫ (x 2 + y 2 )dxdy =

x = ρ cos ϕ

2π

∫∫ ρ2 ρ dϕdρ = ∫ dϕ∫ ρ3dρ =

x 2 +y2 ≤a

y = ρsin ϕ

x 2 +y2 ≤a

2π

2π = πa

∫ dϕ

;

x = ρcos ϕ

2π

∫∫ dxdy =

∫∫ ρ dϕdρ = ∫ dϕ∫ ρdρ =

x2 +y2 ≤a

y = ρsin ϕ

x 2 +y2 ≤a

2π

∫ dϕ

2π = π a 2 .

Для интеграла I2

можно бы и сразу написать

ответ, так как интеграл дает площадь круга с радиусом a .

Итак:

− 6 h 4 πa 2 = 6πha 2 (a 2 − h 3 ).

I = 12 h I1 − 6 h 4 I2 = 12 h πa 4

УЧЕБНО - МЕТОДИЧЕСКИЙ КОМПЛЕКС

РАЗДЕЛ: «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ»

3. Материалы для самостоятельной работы студентов

3.1.КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Определение двойного интеграла.

2.Основные свойства двойного интеграла.

3.Вычисление двойного интеграла в декартовой системе координат

4.Переход из декартовой в полярную систему координат при вычислении двойного интеграла.

5.Определение тройного интеграла.

6.Основные свойства тройного интеграла.

7.Вычисление тройного интеграла в декартовой системе координат.

8.Переход из декартовой в цилиндрическую систему координат.

9.Переход из декартовой в сферическую систему координат при вычислении тройного интеграла.

10.Определение криволинейного интеграла 1-го рода (по длине дуги) и

его свойства.

11.Вычисление криволинейного интеграла 1-го рода (по длине дуги) в

различных видах задания дуги (декартовом, параметрическом, полярном) в

пространстве R 2 и R 3 .

12.Приложения криволинейного интеграла 1-го рода (по длине дуги) к

задачам геометрии и механики.

13.Определение криволинейного интеграла 2-го рода (по координатам) и

его свойства.

14.Вычисление криволинейного интеграла 2-го рода (по координатам) в

различных системах координат.

15.Формула Грина.

16.Условие независимости криволинейного интеграла 2-го рода (по координатам) от формы пути интегрирования.

17.Приложения криволинейного интеграла по координатам к задачам

физики.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1713 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
02.12.2018679 Кб3471-88.doc
#
21.09.201980 Кб43719664.docx
#
22.12.20183 Мб54738_s96.doc
#
17.04.20191 Мб25745_f86.doc
#
01.07.202560 Кб3777786358.docx
#
17.03.20152 Мб297УМК.PDF
#
20.07.20191 Мб98 деятели.rtf
#
01.04.20252 Мб28 Иллюстрация уравнения Бернулли.doc
#
01.07.20254 Мб38 Мех.добыча нефти.doc
#
17.03.2015495 Кб678 Расчет пространственной модели здания.pdf
#
18.09.201979 Кб88 часть.doc