Лодр-з постійними коефіцієнтами

Загальний вигляд: , де. (*)

Для такого рівняння існує спосіб знаходження ФСР, а значить і загального розв’язку.

Частинні розв’язки будемо шукати у вигляді . Це є єдина елементарна функція , всі похідні якої подібні між собою і подібні до самої функції, і тому при підстановці в ЛОДР можуть дати нуль.

Після підстановки маємо: .

Многочлен в дужках називається характеристичним многочленом, який відповідає рівнянню (*). Рівняння називається характеристичним рівнянням. Воно отримане з рівняння (*), якщо замінити похідні різних порядків відповідними степенями .

Отже, буде частинним розв’язком рівняння (*) зі сталими коефіцієнтами, якщоє коренем характеристичного рівняння. Це рівняння маєкоренів, і тому отримаємочастинних розв’язків.

1. всі корені ХР різні (немає кратних коренів) і дійсні, тому всі частинні розв’язки різні між собою.

Покажемо, що розв’язки утворюють ФСР. Складемо детермінант Вронського:

.

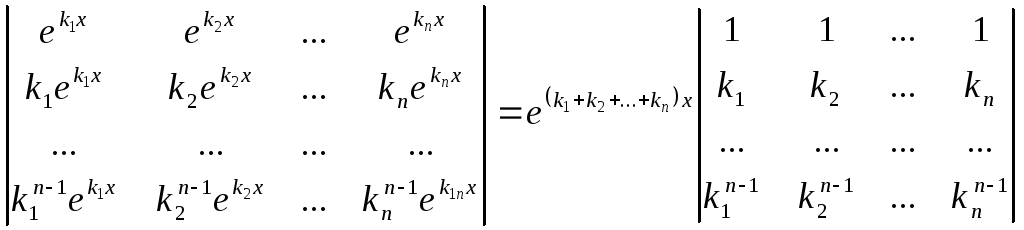Останній визначник є детермінантом Вандермонда, який (як відомо з алгебри) дорівнює і тому при різнихвідмінний від нуля. Отже, системає ФСР і отримаємо загальний розв’язок рівняння у вигляді

.

Приклад. .

, .

2. Розглянемо випадок уявних коренів ХР : . Тоді.

З курсу алгебри відомо, що якщо алгебраїчне рівняння з дійсними коефіцієнтами має комплексний корінь , то воно має і спряжений з им корінь. Тобто маємо два частинні розв’язки:.

За формулою Ейлера маємо,.

Теорема. Якщо ЛОДР-з постійним коефіцієнтами має розв’язок виду, то кожна з функційіє розв’язками цього рівняння.

Доведення. Підставимо в рівняння замість вираз:

Тоді і .

Ця теорема дає висновок, що комплексному кореню відповідає два дійсних розв’язки ЛОДР-:, які є лінійно незалежними. Спряжений корінь дає ті самі (з точністю до множника) дійсні розв’язки.

Отже, кожній парі спряжених комплексних корнів ХР відповідає два дійсних частинних розв’язки .

Приклад. 1) ,

2) ,

3) ХР має кратні корені. Тоді отримаємо менше ніж частинних розв’язків ХР і не отримаємо ФСР і загального розв’язку. Треба знайти новий спосіб.

Розв’язок ДР будемо шукати у вигляді . З певних міркувань після підстановки цього розв’язку в ДР виявляється , що за функціїможна взяти функції, де- кратність кореняХР. Тому частинними розв’язками ДР, що відповідають коренюкратностібудуть функції.

Приклад. ,

3. Якщо маємо - кратну пару спряжених комплексних коренів ХР, то цій парі коренів відповідатимуть такі частинні розв’язки:

,

,

…………………………….

.

Приклад.,

,

Лінійні неоднорідні др-

Це рівняння виду . А рівнянняназиваєтьсявідповідним однорідним ДР-.

Теорема. Якщо - частинний розв’язок ЛНДР-, то його загальний розв’язок буде, де- загальний розв’язок відповідного йому однорідного рівняння.

Доведення проведемо при . Підставимов рівняння:

.

Оскільки - загальний розв’язок відповідного однорідного рівняння, то, а оскільки- розв’язок неоднорідного, то отримаємо тотожність. Отже,- розв’язок ЛНДР-.

Метод варіації довільних сталих знаходження частинного розв’язку лндр-

Суть цього методу з’ясовує наступна теорема, яку доведемо для ЛНДР-2:

Теорема. Щоб отримати частинний розв’язок ЛНДР-2 досить у вираз для загального розв’язкувідповідного однорідного ДР замість сталихіпідставити функціїі, похідні від яких задовольняють систему рівнянь:

.

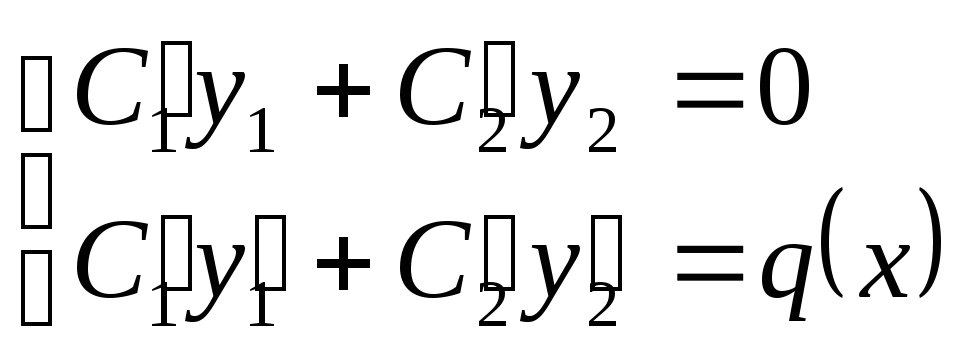Доведення. Якщо , то. Треба знайти функціїі. Одне співвідношення між ними можна взяти довільним. Виберемоітак, щоб. Тоді отримаємоі знайдемо:.

Підставимо в ДР:

,

Оскільки іє розв’язками відповідного однорідного рівняння, тоі. Тому.

Отже, для того, щоб функція була розв’язком ЛНДР-2, необхідно і достатньо, щоб функціїізадовольняли вказану систему. Ця система має розв’язок, оскільки її головний визначник.

Приклад. Нехай задане рівняння , розв’язок відповідного однорідного рівняння якого має вигляд.

Частинний розв’язок неоднорідного рівняння будемо шукати у вигляді . Складемо систему

.