
- •Лекція 1. Основні поняття теорії д.Р.
- •Др 1-го порядку. Основні поняття
- •Метод ізоклін
- •Інтегровні типи др-1, розв’язних відносно похідної
- •Неповні рівняння.
- •Лінійні др-1
- •Загальні властивості розв’язків лодр-1:
- •Рівняння, звідні до лінійних
- •Рівняння в повних диференціалах
- •Інтегрувальний множник
- •Др-1, не розв’язні відносно похідної
- •Рівняння Лагранжа.
- •Др-. Основні поняття та означення
- •Др-, що допускають пониження порядку
- •Лінійні др-
- •Властивості однорідних лінійних др
- •Лодр-з постійними коефіцієнтами
- •Лінійні неоднорідні др-
- •Метод варіації довільних сталих знаходження частинного розв’язку лндр-
- •Лінійні неоднорідні др-зі сталими коефіцієнтами
- •Метод невизначених коефіцієнтів
- •Рівняння Ейлера
- •Інтегрування др за допомогою рядів
- •Системи др Основні означення
- •Метод виключення
- •Метод інтегровних комбінацій
- •Метод Ейлера інтегрування однорідних лінійних систем з постійними коефіцієнтами
- •Метод виключення інтегрування неоднорідних систем лінійних рівнянь
- •Застосування перетворення Лапласа до розв’язування лдр та їх систем
- •Властивості перетворення Лапласа
- •Розв’язування задачі Коші для лінійного др з постійними коефіцієнтами
- •Розв’язування систем лінійних др з постійними коефіцієнтами
- •Інтегральні рівняння
- •Інтегральні рівняння Вольтерра
- •Розв’язування ір Вольтерра за допомогою резольвенти.
- •Метод послідовних наближень
- •Рівняння типу згортки
- •Ір Фредгольма з виродженими ядрами
Др 1-го порядку. Основні поняття
Означення.
ДР
1-го порядку
називається рівняння виду
![]() ,
де
,
де![]() - незалежна змінна,
- незалежна змінна,![]() - невідома функція.
- невідома функція.
Якщо ДР
можна записати у вигляді
![]() ,
то воно називається ДР-1,розв’язним
відносно похідної.
,
то воно називається ДР-1,розв’язним
відносно похідної.
Розв’язком
ДР-1 називається деяка функція
![]() ,
яка при підстановці в дане рівняння
перетворює його в тотожність.Загальним
розв’язком
ДР-1 називається така
,
яка при підстановці в дане рівняння
перетворює його в тотожність.Загальним
розв’язком
ДР-1 називається така![]() функція, що є розв’язком для всіх
можливих значень
функція, що є розв’язком для всіх
можливих значень![]() і для будь-якої початкової умови
і для будь-якої початкової умови![]() існує єдине значення
існує єдине значення![]() ,
при якому розв’язок
,
при якому розв’язок![]() задовольняє цю початкову умову. Розв’язок
задовольняє цю початкову умову. Розв’язок![]() .
Отриманий із загального
.
Отриманий із загального![]() при
при![]() називаєтьсячастинним
розв’язком,
а задачу знаходження частинного розв’язку
ДР
називаєтьсячастинним
розв’язком,
а задачу знаходження частинного розв’язку
ДР
![]() ,
який задовольняє початкову умову
,
який задовольняє початкову умову![]() ,
називаютьзадачею
Коші.
З геометричної точки зору, розв’язати
задачу Коші означає виділити серед всіх
інтегральних кривих даного ДР ту
інтегральну криву, яка проходить через
точку
,
називаютьзадачею
Коші.
З геометричної точки зору, розв’язати
задачу Коші означає виділити серед всіх
інтегральних кривих даного ДР ту
інтегральну криву, яка проходить через
точку
![]() .
.
Приклад.
Перевірити, що функція
![]() є загальним розв’язком ДР
є загальним розв’язком ДР![]() та знайти частинний розв’язок, що
задовольняє початковій умові
та знайти частинний розв’язок, що
задовольняє початковій умові![]() .
Дати геометричне тлумачення результату.
.
Дати геометричне тлумачення результату.
Якщо
задача Коші має не один розв’язок або
ж зовсім його не має, то кажуть, що в
точці
![]() порушується єдність розв’язку задачі
Коші.
порушується єдність розв’язку задачі
Коші.
Справедлива теорема
Теорема
Пікара.
Нехай
функція
![]() в ДР-1
в ДР-1![]() визначена і неперервна в обмеженій
області
визначена і неперервна в обмеженій
області![]() і отже, вона є обмеженою, тобто
і отже, вона є обмеженою, тобто![]() .
І функція
.
І функція![]() має обмежену частинну похідну по змінній
має обмежену частинну похідну по змінній![]() в області
в області![]() :
:![]() .
Тоді задача Коші має єдиний
неперервно-диференційонвний розв’язок
в інтервалі
.
Тоді задача Коші має єдиний
неперервно-диференційонвний розв’язок
в інтервалі![]() ,
де
,
де![]() .
.
Ця
теорема дає достатні умови існування
єдиного розв’язку задачі коші для ДР-1,
але вони не є необхідними: може існувати
єдиний розв’язок задачі Коші для ДР-1,
але в точці
![]() наведені умови не виконуються.
наведені умови не виконуються.
Зауваження.
Умова обмеженості похідної
![]()
![]() може бути дещо послаблена та замінена
умовою Ліпшіца.
може бути дещо послаблена та замінена
умовою Ліпшіца.
Означення.
Кажуть,що функція
![]() ,
визначена в області
,
визначена в області![]() ,
задовольняє в цій областіумові
Ліпшіца
по змінній
,
задовольняє в цій областіумові
Ліпшіца
по змінній
![]() ,
якщо існує така стала
,
якщо існує така стала![]() (константа Ліпшіца), що для всіх
(константа Ліпшіца), що для всіх![]() і
і![]() виконувалась нерівність
виконувалась нерівність![]() .
.
Приклад.
![]() .
Тут
.
Тут![]() недиференційовна по змінній
недиференційовна по змінній![]() в точці
в точці![]() б
б![]() ,
але умова Ліпшіца в околі цієї точки
виконується:
,
але умова Ліпшіца в околі цієї точки
виконується:
![]() ,
,
оскільки
![]() .
Тут
.
Тут![]()
![]() .
.
Теорема
Коші.
Якщо
функція
![]() неперервна і задовольняє умові Ліпшіца
по змінній
неперервна і задовольняє умові Ліпшіца
по змінній![]() в області
в області![]() ,
то задача Коші для ДР-1 має єдиний
розв’язок.
,
то задача Коші для ДР-1 має єдиний
розв’язок.
Означення.
Функція
![]() називається особливим розв’язком ДР-1,
якщо:
називається особливим розв’язком ДР-1,
якщо:
вона є розв’язком цього рівняння;
через кожну точку кривої
 проходить принаймні дві різних
інтегральних кривих цього рівняння.
проходить принаймні дві різних
інтегральних кривих цього рівняння.
Виникають питання:
чи кожне ДР має особливий розв’язок?
Якщо має, то як його знайти?
Відповідь на перше питання негативна, оскільки ДР, що задовольняють умови теорем Пікара або Коші особливих розв’язків не мають.
Для відповіді на друге питання введемо поняття.
Означення
Нехай задана одно параметрична сім’я
кривих
![]() .
Крива
.
Крива![]() називається обвідною цієї сім’ї, якщо:
називається обвідною цієї сім’ї, якщо:
для довільної точки кривої
 існую крива з цієї сім’ї
існую крива з цієї сім’ї ,
яка до неї дотикається в цій точці;
,
яка до неї дотикається в цій точці; складається
лише з таких точок.
складається
лише з таких точок.
З
диф.геометрії відомо, що якщо сім’я
кривих
![]() має обвідну, то її можна знайти, виключивши
параметр
має обвідну, то її можна знайти, виключивши
параметр![]() із системи:
із системи:

Приклад.
Знайти обвідну сім’ї парабол
![]() .
.
Маємо

Особливі
розв’язки ДР-1 треба шукати там, де
порушується умова теореми Пікара або
Коші (зокрема, умова Ліпшіца чи обмеженість
похідної
![]() ).
).
Зауваження.
Точки, в яких
![]() необмежена, можуть і не складати особливих
розв’язків.
необмежена, можуть і не складати особливих
розв’язків.
Приклад.
![]()
![]() не є
особливим розвєєязком, оскільки ця
функція навіть не є розв’язком ДР.
не є
особливим розвєєязком, оскільки ця
функція навіть не є розв’язком ДР.
Теорема.
Якщо
![]() є загальний розв’язок рівняння
є загальний розв’язок рівняння![]() і сім’я кривих
і сім’я кривих![]() має обвідну
має обвідну![]() ,
то ця обвідна буде особливим розв’язком
ДР-1.
,
то ця обвідна буде особливим розв’язком
ДР-1.
Приклад.
Знайти особливий розв’язок рівняння
![]() .
.
Загальний
розв’язок рівняння має вигляд
![]() - сім’я прямих.
- сім’я прямих.
Побудувати декілька .
Складемо
систему
 ,
,![]() ,
,
Тоді
![]()
![]() - парабола.
- парабола.
Можна перевірити, що ця функція є розв’язком.
Зауваження.
Інколи при інтегруванні отримуємо
сімейство інтегральних кривих, залежне
від сталої
![]() ,
в параметричній формі
,
в параметричній формі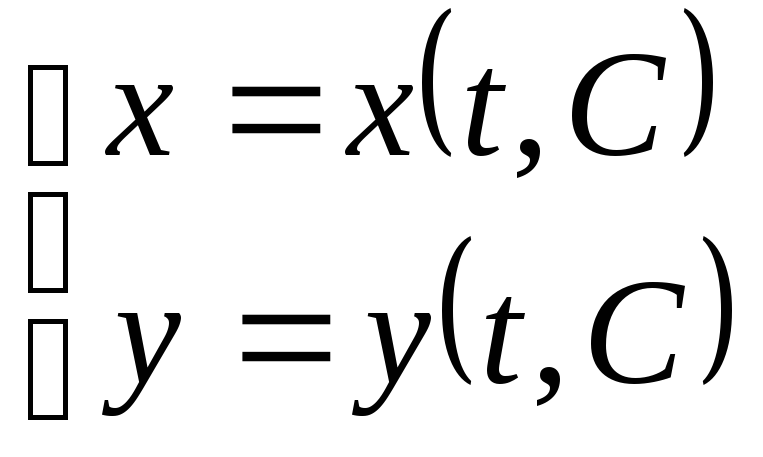 .
Таке сімейство інтегральних кривих
називаєтьсязагальним
розв’язком
ДР-1 в параметричній
формі.
Якщо можна виключити параметр
.
Таке сімейство інтегральних кривих
називаєтьсязагальним
розв’язком
ДР-1 в параметричній
формі.
Якщо можна виключити параметр
![]() ,
то отримаємо загальний розв’язок в
неявному або явному вигляді.
,
то отримаємо загальний розв’язок в
неявному або явному вигляді.
