Інтегровні типи др-1, розв’язних відносно похідної

1. Неповні рівняння.

А) ДР-1, що не містять шуканої функції .

Нехай - неперервна на. Тоді загальний розв’язокв області. Особливих розв’язків рівняння не має.

Розглянемо задачу Коші з початковими умовами . Проінтегруємо рівняння віддо:/

Якщо має розрив в деякій точці, то замість ДРрозглядають рівняння. Прямає розв’язком цього рівняння і цей розв’язок треба приєднати до розв’язку початкового рівняння. Він може бути частинним (отриманий із загального при деякому) або особливим.

Б) ДР-1, яке не містить незалежної змінної: .

Нехай неперервна на. Тоді замість цього рівняння розглянемо рівняння, що є рівнянням, що не містить шуканої функції А).

Якщо при ,функціянеперервна і, то розв’язокє або частинним або особливим.

Приклад. .

Область визначення рівняння є .

, ,,.

2. Рівняння з відокремлюваними змінними.

Рівняння виду називається рівнянням звідокремлюваними змінними. Припустимо, що . Тоді розділимо ліву частину рівняння на цей вираз, отримаємо:

,

який можна переписати так: 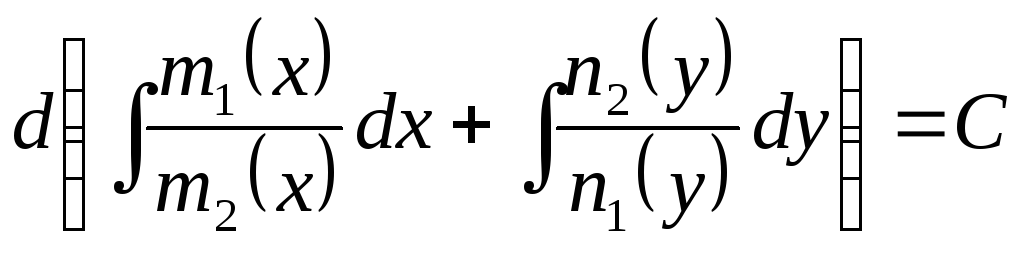- загальний інтеграл.

Якщо врахувати початкові умови , отримаємо розв’язок задачі Коші

.

При діленні на вираз можна загубити розв’язки, які визначаються рівняннямиі. Якщо ці розв’язки не входять до загального інтегралу, то вони є особливими розв’язками.

Приклад.

Розв’язок є особливим.

Приклад. Знайти частинний розв’язок рівняння , що задовольняє початкову умову.

Якщо , то,.

Приклад. Знайти криву, що проходить через точку , щоб тангенс кута нахилу дотичної в довільній її точці дорівнював ординаті цієї точки, збільшеній на 3 одиниці.

Маємо ДР , що випливає з геометричного змісту похідної. Його розв’язок.

Використаємо початкову умову :.

Приклад. Відомо, що швидкість розпаду радію прямо пропорційна його кількості. Визначити залежність кількості радію від часу.

Позначимо через кількість радію в момент часу, тодішвидкість розпаду радію. За умовою отримаємо ДР. Це є р-ня з відокремлюваними змінними. Загальний розв’язок:.

Нехай в деякий момент часу булограмів радію. Тоді отримаємо.

3. Однорідні ДР-1 та звідні до них

Означення. Функція називаєтьсяоднорідною функцією виміру , якщо. Якщо ця рівність виконується при, тоназивається додатньо однорідною.

Приклад. .

Означення. ДР-1 називаєтьсяоднорідним, якщо функції таоднорідні одного виміру.

Однорідне рівняння завжди можна звести до рівняння виду , в якому функція- однорідна нульового виміру. Такі рівняння завжди інтегруються в скінченному вигляді, ввівши підстановку, в результаті чого отримуємо рівняння з відокремлюваними змінними.

Дійсно,

,

,

,

Позначимо , отримаємо

, ,

При відокремленні змінних можна було втратити розв’язки , де- корені рівняння. Отже, пів прямі, а також півосі вісіможуть бути частинними розв’язками ДР, якщо їх можна отримати із загального, або особливими. Інших особливих розв’язків ДР не має.

Приклад.

Введемо підстановку ,

, ,

- особливий розв’язок (його не можна дістати із загального при будь-якому значенні ).

Рівняння виду зводиться до однорідного в наступних випадках:

1) , то це і є однорідне рівняння

2)хоча б одне з чисел абовідмінне від нуля:

А)

Проведемо заміну , де- нові змінні,- параметри. Тоді

.

Параметри виберемо з умови. Оскільки, то ця система має єдиний розв’язок. Отримаємо однорідне ДР

.

Б)

Заміною останнє ДР приводимо до рівняння з відокремлюваними змінними

,

Приклад. Знайти загальний розв’язок рівняння .

Складемо систему ,

Система має єдиний розв’язок . Тому вводимо заміну, після якої рівняння приймає вигляд

- однорідне рівняння.

, .

Покладемо , тодіі.

, ,

, ,,

, ,

,

- загальний інтеграл.

Приклад. Знайти загальний розв’язок рівняння .

Складемо систему , для якої. Введемо підстановку, тому,,.

Отримаємо рівняння ,

,

, ,

.

Інколи рівняння можна привести до однорідного заміною змінних . Це має місце в тому випадку, коли в рівнянні всі члени є одного виміру, якщо зміннійприписати вимір 1, змінній- вимір, похідній- вимір(або відповідно диференціаламтавимірита). Такі рівняння називаютьсяузагальнено-однорідними.

Приклад. Знайти загальний розв’язок .

Покладемо , тоді,- довільне число, яке виберемо пізніше.

,

Дане рівняння буде однорідним, якщо всі члени мають однаковий вимір, тобто ,. Тому підстановка приймає вигляд,і

, ,

- однорідне рівняння