Метод Ейлера інтегрування однорідних лінійних систем з постійними коефіцієнтами

Означення. Лінійною однорідною системою з постійними коефіцієнтами називається система ДР вигляду ,, де коефіцієнти- деякі сталі,- шукані функції.

Дану систему можна записати у матричній формі , де

.

Матриця-стовбець називаєтьсячастинним розв’язком матричного рівняння, якщо виконується тотожність для.

Система частинних розв’язків

,

(,- номер розв’язку,- номер функції у розв’язку) називаєтьсяфундаментальною на , якщовизначник Вронського

.

Теорема. Якщо система частинних розв’язків однорідного матричного рівняння є фундаментальною, то загальний розв’язок цього рівняння має вигляд , де- довільні сталі.

Метод Ейлера розглянемо на прикладі системи 3-х лінійних рівнянь.

Розв’язок системи будемо шукати у вигляді ,- сталі. Підставимо їх в систему і скоротимо на:

(**)

Ця система має ненульовий розв’язок, якщо її визначник . Це рівняння називається характеристичним.

Можливі наступні випадки:

1. Корені характеристичного рівняння дійсні і різні. Підставляючи в систему (**) замістьчислапоступово отримаємо числавідповідно, яким будуть відповідати трійки частинних розв’язків:

Загальний розв’язок системи має вигляд

.

Приклад. . ХР:.

1)

2)

3)

Тоді загальний розв’язок має вигляд .

2. корені ХР рівняння комплексні .

Маємо ХР: .

1). Виберемо перше рівняння і покладемо.

2)

Перейдемо до нової фундаментальної системи розв’язків за формулами:

Тоді .

І загальний розв’язок отримається

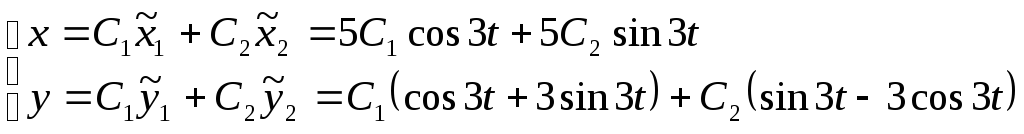
Зауваження. Знайшовши перший частинний розв’язок, можна було б відразу написати загальний розв’язок системи за формулами:

.

Для попереднього прикладу отримаємо:

3. випадок кратних коренів.

Приклад. Розв’язати систему

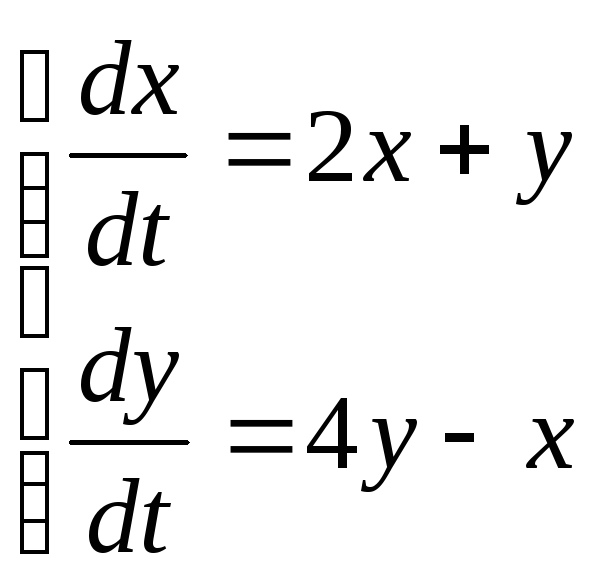
ХР: .

Розв’язок будемо шукати у вигляді . Підставимо ці рівності в перше рівняння системи:

Прирівняємо коефіцієнти при однакових степенях :

і є довільними, позначимо їх черезі. Отримаємо.

Відповідь:

Метод виключення інтегрування неоднорідних систем лінійних рівнянь

Приклад.

Застосування перетворення Лапласа до розв’язування лдр та їх систем

Означення. Функцією-оригіналом називають функцію , що задовольняє умови:

1) , якщо;

2) інтегровна на довільному скінченному інтервалі вісі;

3) зі зростанням модульзростає не швидше деякої показникової функції, тобто існують числаі:.

До таких функцій, зокрема, відносяться всі обмежені функції, всі неперервні функції.

Означення. Зображенням функції-оригінала за Лапласом називається функція , визначена рівністю.

Перетворення , що ставить у відповідність оригіналуйого зображення, називаєтьсяперетворенням Лапласа: .

Приклад. Знайти зображення функції Хевісайда .

.

Властивості перетворення Лапласа

Нехай .

1. Властивість лінійності: для .

2. Теорема подібності: для .

3. Теорема запізнення: для довільного .

4. Теорема зміщення (множення оригіналу на показникові функцію): для довільного .

5. Диференціювання оригіналу: якщо оригінал, то.

6. Якщо разів неперервно-диференційовна наіє оригіналом, то.

7. Інтегрування оригіналу зводиться до ділення зображення на , тобто.

8. Інтегрування зображення рівносильне діленню на оригіналу:

(за умови збіжності інтегралу ).

9. Теорема множення. Добуток двох зображень ітакож є зображенням, причому.

Інтеграл справа називається згорткою функцій і:.

Приклади. За теоремою зміщення .

Відомо, що . Оскільки, то,

За теоремою подібності ,.

За теоремою зміщення .

За теоремою про диференціювання зображення:

, ,,, …,.

За теоремою зміщення .

Для знаходження оригіналу за відомим зображеннямзастосовується наступне правило:даний дріб розкладається в суму елементарних дробів і знаходять для кожного з них оригінал.

Приклад. Знайти оригінал , якщо.

.

Маємо . Тому.