
- •Кафедра высшей математики
- •Операции над матрицами
- •Обратная матрица
- •Ранг матрицы
- •1.Что такое матрица?
- •Определителем квадратной матрицы n-го порядка называется число, равное следующей сумме:
- •Минором элементаквадратной матрицыn-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы а вычеркиванием I-й строки и j-го столбца.
- •Алгебраическим дополнением элементаквадратной матрицыn-го порядка называется его минор, взятый со знаком :
- •Свойства определителей
- •Лекция № 5 - 7
- •Система n линейных уравнений с n переменными. Метод обратной матрицы и формулы Крамера
- •Метод Гаусса
- •Лекция № 8 - 9 Векторная алгебра
- •Векторы и операции над ними
- •Разность векторов и- это сумма вектораи вектора
- •Размерность и базис векторного пространства
- •Переход к новому базису
- •Евклидово пространство Скалярным произведением двух векторов иназывается число:
- •Линейные операторы
- •Собственные векторы и собственные значения линейного оператора
- •Линейная модель обмена (модель международной торговли)
- •Лекция № 10 - 12 Аналитическая геометрия
- •Уравнение прямой
- •Примерные тесты
- •VII. Учебно - методическое обеспечение дисциплины
Линейные операторы
Рассмотрим два
линейных пространства:
![]() размерности
размерности![]() и
и![]() размерности
размерности![]()
Если задан закон
( правило), по которому каждому вектору
![]() ставится в соответствие единственный
вектор
ставится в соответствие единственный
вектор![]() то
говорят, что заданоператор
( преобразование, отображение) А ( х ),
действующий из
то
говорят, что заданоператор
( преобразование, отображение) А ( х ),
действующий из
![]() в
в![]() ,
и записывают у=А( х).
,
и записывают у=А( х).
Оператор называется
линейным , если для любых векторов
![]() выполняются
соотношения:
выполняются
соотношения:
1.
![]() свойство
аддитивности;
свойство
аддитивности;
2.
![]() свойство
однородности оператора.
свойство
однородности оператора.
Вектор
![]() называется образом вектора х, а сам
вектор х- прообразом вектора
называется образом вектора х, а сам
вектор х- прообразом вектора![]()
Если пространства
![]() и
и![]() совпадают, то оператор А отображает
пространство
совпадают, то оператор А отображает
пространство![]() в себя. Рассмотрим именно этот случай.
в себя. Рассмотрим именно этот случай.
Выберем в
![]() базис
базис![]() запишем
разложение произвольного вектора
запишем
разложение произвольного вектора![]() по этому базису:
по этому базису:
![]()
Применим к этому
выражению линейный оператор
![]() в силу его линейности получаем:
в силу его линейности получаем:
![]()
Поскольку
![]() -также
вектор из
-также
вектор из![]() то
его можно разложить по базису
то
его можно разложить по базису![]() :
:
![]()
Тогда
![]()
Перегруппируем
сомножители в правой части, вынося за
скобки базисные векторы
![]() получим:
получим:
![]() (*)
(*)
С другой стороны,
вектор
![]() имеющий в том же базисе
имеющий в том же базисе![]() координаты
координаты![]() можно записать так:
можно записать так:
![]() (**)
(**)
Разложение вектора по базису единственно, следовательно, правые части (*) и (**) равны, поэтому:
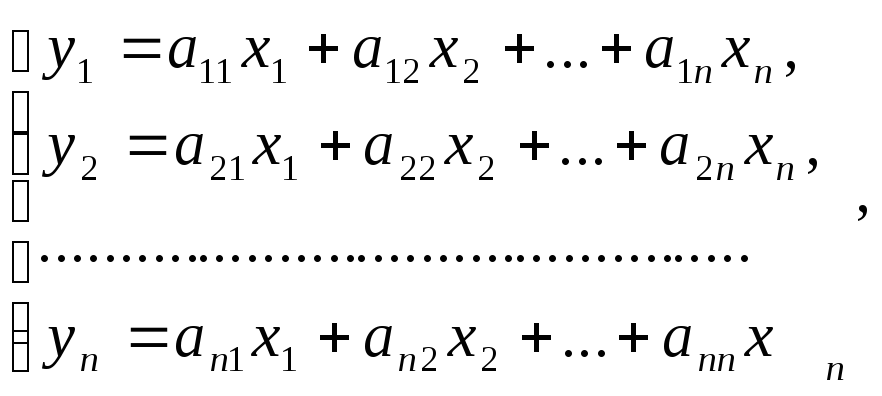
или в матричной
форме:
![]()
Матрица
![]() каждый
столбец которой состоит из координат
образа
каждый
столбец которой состоит из координат
образа![]() соответствующего базисного вектора
соответствующего базисного вектора![]() в том же базисе
в том же базисе![]() называетсяматрицей
оператора
называетсяматрицей
оператора
![]() в базисе
в базисе![]() ,
а рангr
матрицы А рангом оператора
,
а рангr
матрицы А рангом оператора
![]() .
.
Таким образом, каждому линейному оператору соответствует матрица в данном базисе. Наоборот, всякой матрице n-го порядка соответствует линейный оператор n-мерного пространства.
Вектор х и его
образ
![]() связаны матричным уравнением:
связаны матричным уравнением:
![]()
где А- матрица
линейного оператора
![]() .
.
Пример:
Линейный оператор
![]() в
в![]() в базисе
в базисе![]() задан матрицей
задан матрицей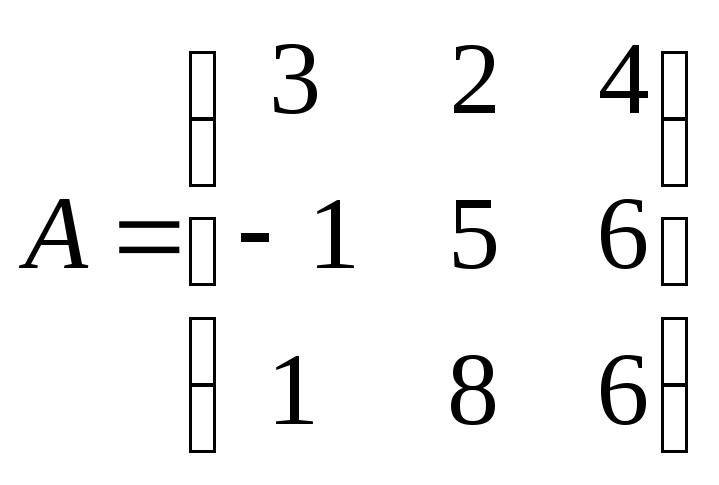 Найти образ
Найти образ![]() вектора
вектора![]()
Решение:
Применяем
формулу перехода:

Образ вектора х
имеет вид:
![]()
Суммой двух
линейных операторов
![]() и
и![]() называется оператор
называется оператор![]() определяемый
равенством:
определяемый
равенством:
![]()
Произведением
линейного
оператора
![]() на число
на число![]() называется оператор
называется оператор![]()
Произведением
линейных
операторов
![]() и
и![]() называется оператор
называется оператор![]()
![]()
Все эти операторы удовлетворяют свойствам аддитивности и однородности, т.е. являются линейными.
Нулевой оператор
![]() переводит
все векторы из
переводит
все векторы из![]() в
нулевые векторы
в
нулевые векторы![]()
Тождественный
оператор
![]()
Теорема.
Матрицы
![]() и
и![]() линейного оператора
линейного оператора![]() в базисах
в базисах![]() и
и![]() ,
,![]() связаны
соотношением:
связаны
соотношением:![]() где
где![]() матрица
перехода от старого базиса к новому.
матрица
перехода от старого базиса к новому.
Пример.В базисе![]() оператор
оператор![]() имеет матрицу
имеет матрицу![]() .
Найти матрицу оператора
.
Найти матрицу оператора![]() в базисе
в базисе
![]()
![]()
Решение,
Матрица перехода здесь
![]() ,
а обратная к ней
,
а обратная к ней![]()
Следовательно,
![]()
Собственные векторы и собственные значения линейного оператора
Вектор
![]() называетсясобственным
вектором
линейного оператора
называетсясобственным
вектором
линейного оператора
![]() если
найдется такое число
если
найдется такое число![]() что
что
![]() (*)
(*)
Число
![]() называетсясобственным
значением оператора
называетсясобственным
значением оператора
![]() ( матрица А), соответствующим вектору
( матрица А), соответствующим вектору![]() Под действием линейного оператора
Под действием линейного оператора![]() собственный вектор переходит в вектор,
коллинеарный самому себе.
собственный вектор переходит в вектор,
коллинеарный самому себе.
Перепишем (*) в
матричной форме:![]()
В развернутом виде:

Представим в однородном виде:

Эта система (однородная) всегда имеет нулевое ( тривиальное) решение х=0. Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы равнялся нулю:
 = 0
(**)
= 0
(**)
Определитель
![]() является многочленомn-ой
степени относительно
является многочленомn-ой
степени относительно
![]() Это – характеристический многочлен
оператора
Это – характеристический многочлен
оператора![]() или матрицы А, а уравнение (**) –
характеристическое уравнение оператора
или матрицы А, а уравнение (**) –
характеристическое уравнение оператора![]() или матрицы А.
или матрицы А.
Характеристический
многочлен линейного оператора не зависит
от выбора базиса, т.е.
![]() где
где![]() матрицы
оператора
матрицы
оператора![]() в старом и новом базисах соответственно.
в старом и новом базисах соответственно.
Пример.
Найти собственные значения и собственные
векторы линейного оператора
![]() заданного
матрицей
заданного
матрицей

 1 4
1 4
А = 9 1 .
Решение. Составим характеристическое уравнение
![]() ,
или
,
или
![]() откуда
откуда![]()
Находим собственный
вектор
![]() отвечающий собственному значению
отвечающий собственному значению![]()
![]() или
или
![]()
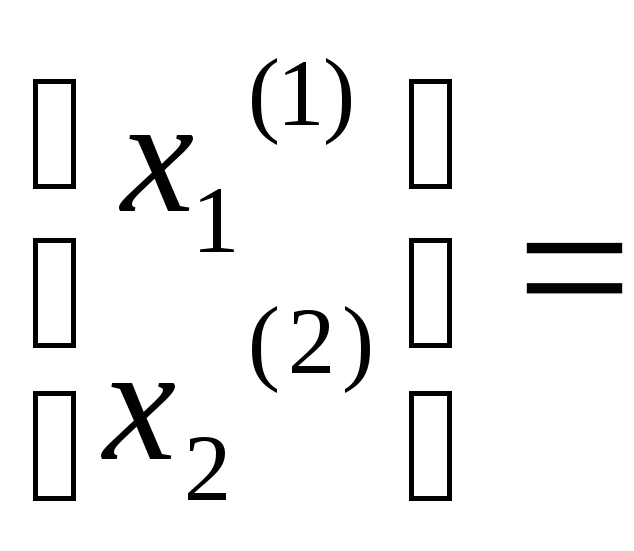
![]() ,
откуда
,
откуда![]() Примем
Примем![]() отсюда
векторы
отсюда
векторы![]()
![]() являются собственными векторами
линейного оператора
являются собственными векторами
линейного оператора![]() с собственным значением
с собственным значением![]()
Аналогично для
![]() векторы
векторы![]()
![]() являются собственными векторами
линейного оператора
являются собственными векторами
линейного оператора![]() с собственным значением
с собственным значением![]()
Наиболее простой
вид принимает матрица А линейного
оператора
![]() ,
имеющегоn
линейно независимых собственных векторов
,
имеющегоn
линейно независимых собственных векторов
![]() с собственными значениями , соответственно
равными
с собственными значениями , соответственно
равными![]() Матрица оператора
Матрица оператора![]() в базисе, составленном из его собственных
векторов, является диагональной и имеет
вид:
в базисе, составленном из его собственных
векторов, является диагональной и имеет
вид:
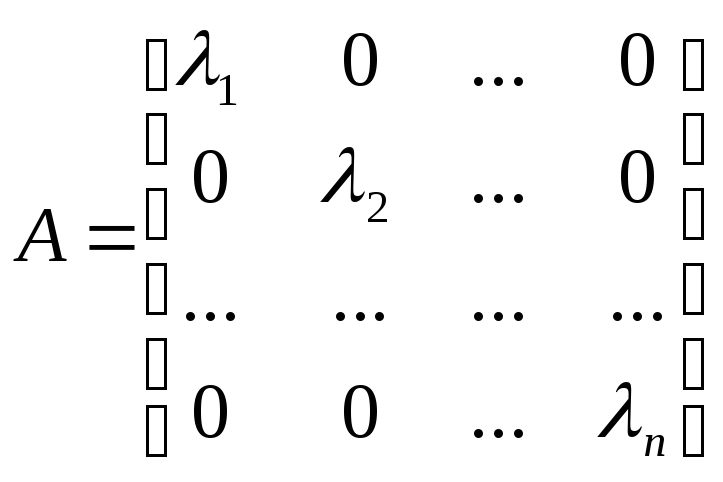
Верно и обратное:
если матрица А линейного оператора
![]() в некотором базисе является диагональной
, то все векторы этого базиса – собственные
векторы оператора
в некотором базисе является диагональной
, то все векторы этого базиса – собственные
векторы оператора![]()
Кроме того, если линейный оператор имеет n попарно различных собственных значений , то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
