Линейная модель обмена (модель международной торговли)

Пусть n стран имеют национальный доходсоответственно,доля национального дохода, которуюj-ая страна тратит на покупку товаров у I-ой страны. Считаем, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.

(1)

Матрицаназываетсяструктурной матрицей торговли.

В соответствии с выражением (1) сумма элементов любого столбца равна единице.

Для I-ой страны выручка от внутренней и внешней торговли составит:

Для сбалансированной торговли необходима бездефицитность торговли каждой стран, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:

Отсюда получаем систему неравенств:

(2)

Сложим все неравенства, получим после группировки:

Учитывая (1), имеем

Неравенство невозможно, условиепринимает видС экономической точки зрения это означает, что все страны не могут одновременно получать прибыль.

Введем вектор х=((вектор- столбец), получим уравнение

(3)

Задача сводится к отысканию собственного вектора матрицы А, отвечающего собственному значению

Пример. Структурная матрица торговли трех стран имеет вид:

Найти национальные доходы стран для сбалансированной торговли.

Решение. Решим уравнение

=

Методом Гаусса найдем решение: т.е.

Для сбалансированной торговли соотношение национальных доходов должно быть или 3:4:2.

Вопросы для самоконтроля:

1. Что такое вектор?

2. Назовите основные операции над векторами, их свойства

3. Что такое базис?

4. Как найти собственные векторы и собственные числа линейного оператора.

5. Для самостоятельного изучения - линейная модель обмена (Балансовый анализ)

Лекция № 10 - 12 Аналитическая геометрия

План лекции

1. Основные понятия для вывода уравнения прямой

2. Способы задания уравнения прямой на плоскости и в пространстве

3. Взаимное расположение прямых

Уравнением линии (кривой) на плоскости O_xy называется уравнение, которому удовлетворяют координаты x и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на это линии.

В общем виде уравнение линии:

F (x,y) = 0

или, если это возможно:

у = f (x).

Любую линию на плоскости можно выразить соответствующим уравнением, но не всякое уравнение определяет на плоскости некоторую линию.

Уравнение прямой

Пусть прямая пересекает ось Оу в точке В (о; в) и образует с осью Ох угол a (0<a<)

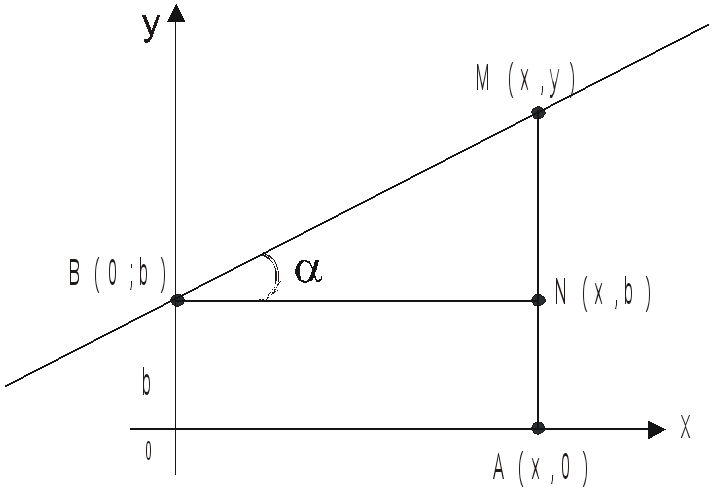
Уравнение прямой можно записать так: у = kх +b,

где tga = k = - угловой коэффициент прямой. Это – уравнение прямой с угловым коэффициентом. Формула справедлива и для

< a < p.

Частные случаи (1):

1. b = 0; у = kx – уравнение прямой, проходящей через начало координат;

2. a = 0; k = tg 0 = 0; у = в – уравнение прямой, параллельной оси О_х;

3. a =-вертикальная прямая, у которой не существует углового коэффициента; х = а, прямая пересекает ось О_х в точке х = а.

Уравнение произвольной прямой, проходящей через точку М₁ (х₁,у₁) с координатами х₁ и у₁, имеет вид:

у – у₁ = k (x –x₁). (2)

Здесь k – произвольное число; задав его, можно задать конкретную прямую. Это уравнение называется также уравнением пучка прямых.

Прямую можно задать координатами двух точек, через которые она проходит:

(3)

где х₁, у₁ – координаты первой точки М₁, х₂, у₂ – координаты второй точки М₂.

Еще один способ задать уравнение прямой – выразить его через отрезки, которые прямая отсекает на осях координат:

(4)

Уравнение (4) называется уравнением прямой в отрезках.

Наиболее общим способом задать уравнение прямой является общее уравнение 1-й степени с двумя переменными:

Ах + Ву + С = О, (5).

в котором А и В не равны нулю одновременно, т.е. А² + В² ¹ 0.

Частные случаи уравнения (5):

1. В ¹ 0, тогда

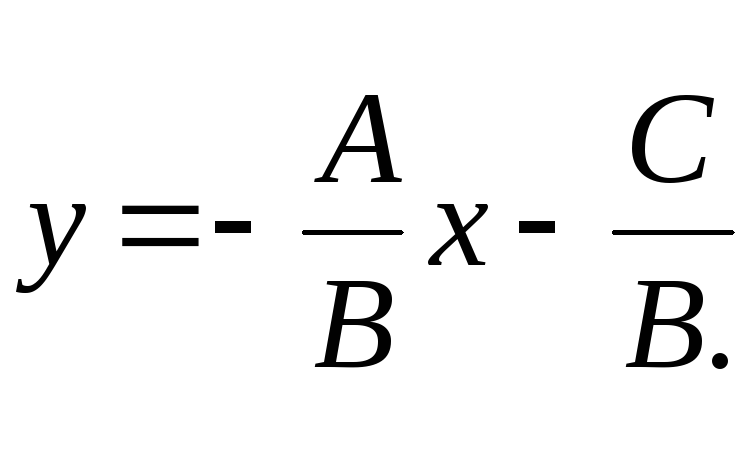
Это уравнение (1), в котором

Если A¹0, С=0, тогда y=kx (прямая проходит через начало координат);

А=0, С¹0, у=b –прямая параллельна оси О_х;

2. В=0, А¹0, тогда

с¹0, х=а – прямая параллельна оси О_у;

с=0, х=0 – уравнение оси О_у.

Таким образом уравнение (5) при любых допустимых значениях А, В, С есть уравнение некоторой прямой линии на плоскости О_ху. Это общее уравнение прямой.

Пусть заданы две прямые:

y=k₁x+b₁

y=k₂x+b₂.

Тогда угол j между этими прямыми (j=a₂-a₁, a₁¹,a₂¹) определяется выражением:

(6).

Угол j получается поворотом против часовой стрелки первой прямой до совпадения со второй. Из выражения (6) условие параллельности двух прямых:

к₁ = к₂ (7),

а условие перпендикулярности –

к₁ к₂ = -1. (8)

Если прямые заданы общим уравнениями

А₁ х + В₁ у + С₁ = 0

А₂ х + В₂ у + С₂ = 0,

условие параллельности имеет вид:

, (9)

а условие перпендикулярности –

А₁ А₂ + В₁ В₂ = 0. (10)

При этом если прямые не параллельны, координаты точки их пересечения можно найти из решения системы уравнений:

Точка пересечения в этом случае будет единственной.

Если дано уравнение прямой в общем виде Ах + Ву + С = 0 и координаты точки М (х_о,у_о), не лежащей на этой прямой, то расстояние от точки М до прямой определяется выражением:

Вопросы для контроля:

1. Запишите различные виды уравнения прямой на плоскости и в пространстве.

2. Запишите условие параллельности и перпендикулярности прямых