«Институт экономики, управления и права (г. Казань)»

Кафедра высшей математики

ЛЕКЦИИ

ПО

ЛИНЕЙНОЙ АЛГЕБРЕ

Преподаватель: Платонова Татьяна Евгеньевна,

кандидат педагогических наук, доцент кафедры высшей математики

Зеленодольск - 2014

СОДЕРЖАНИЕ

I. Матрицы и операции над ними……………………………………………… 3

II. Определители и их свойства………………………………………………. 10

III. Системы линейных алгебраических

уравнений…………………………………………………………………...15

IV. Элементы векторной алгебры………………………………… ………….22

V. Аналитическая геометрия…………………………………………………..33

VI. Примерные тесты и практические задания ………………………………37

VII. Учебно-методическое обеспечение ………………………………………43

Лекция №1-2

Матрицы. Основные сведения о матрицах.

План:

1. Основные понятия и определения

2. Операции над матрицами

3. Обратная матрица

4. Ранг матрицы

Значительную часть математических моделей в экономике можно записать в компактной матричной форме.

Матрица размера mn – это прямоугольная таблица чисел, содержащая m строк и n столбцов . Сами числа называются элементами матрицы.

Обозначаются матрицы прописными буквами латинского алфавита: А,В,С,… ,

элементы –соответствующими строчными буквами с индексами-,…, гдеi- номер строки, j-номер столбца:

, или

Например,

Две матрицы А и В называются равными, если они имеют одинаковую размерность ( т.е. количество строк и количество столбцов) и одинаковые соответствующие элементы: для любых;.( в дальнейшем вместо слова “любой” будем записывать значок).

Рассмотрим частные виды матриц:

• матрица-строка состоит из одной строки, т.е. имеет размерность ;

• матрица-столбец состоит из одного столбца, т.е. имеет размерность ;

• квадратная матрица n-го порядка имеет одинаковое количество строк и столбцов,т.е. размерность ;

• диагональная матрица- это квадратная матрица, у которой все элементы, стоящие вне главной диагонали, равны нулю, а диагональные элементы не равны нулю,т.е. 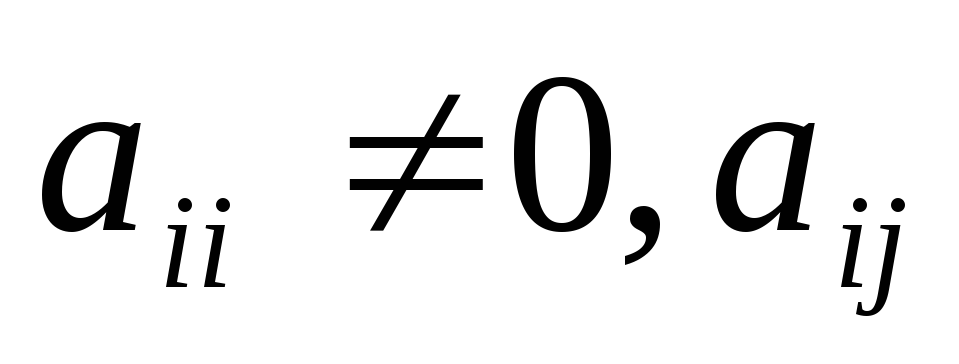=0 , если;все элементы,образуютглавную диагональ;

• единичная матрица n-го порядка - частный случай диагональной, в которой все диагональные элементы равны единице; обычно единичная матрица обозначается Е или I;

• нулевая матрица (нуль-матрица) – это матрица, у которой все элементы равны нулю; такая матрица может быть любого размера.

Операции над матрицами

1. Умножение матрицы на число. Произведение матрицы А и числа равно матрице В той же размерности, что и А, каждый элемент которой получается умножением соответствующего элемента матрицы А на, т.е.;.

Например,

Следствие: общий множитель всех элементов матрицы можно выносить за знак матрицы:

При умножении матрицы на нуль получается нуль-матрица.

2. Сложение матриц. Складывать можно только матрицы одинаковой размерности, для матриц разных размерностей операция не определена.

Суммой двух матриц А и В одинакового размера называется матрица С=А+В размера, элементы которой,;

,т.е. матрицы складываются поэлементно.

Пример:

3. Вычитание матриц: Определяется через предыдущие операции:

А-В=А+(-1)В

4. Умножение матриц. Умножение матрицы А на матрицу В определено , когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц называется такая матрица, каждый элемент которойравен сумме произведений элементовой строки матрицы А на соответствующие элементыго столбца матрицы В:

;

( Здесь означает суммирование по всем значениям номеровs, изменяющихся от 1 до к включительно).

Пример: вычислить произведение матриц АВ, где

Прежде всего убедимся, что такая операция возможна: и, число столбцов матрицы А равно числу строк матрицы В; далее, размерность результирующей матрицы

Вычислим элементы матрицы- произведения:

Свойства операции над матрицами:

1. А+В = В+А

2. (А+В)+С= А+(В+С)

3. (А+В)=

4. А (В+С)=АВ+АС

5. (А+В)С=АС+ВС

6. 

7. А(BC)=(AB)C

Эти свойства аналогичны свойствам операций над числами. Однако некоторые свойства отличаются:

• если произведение АВ существует, то ВА может не существовать, например, матрица и

• если даже АВ и ВА существую, то они могут быть матрицами разных размеров;

Например: ,

таким образом, АВВА

• даже если АВ и ВА существуют и являются матрицами одинакового размера , то , вообще говоря, АВВА ( произведение матриц не коммутативно); например:

Частный случай: произведение любой квадратной матрицы А на единичную Е того же порядка коммутативно, т.е. АЕ=ЕА=А;

• произведение двух ненулевых матриц может равняться нулевой матрице:

5. Возведение в степень. Операция определена только для квадратных матриц:

( m сомножителей);

здесь m-целое.

По определению полагают, что ;

;

6. Транспонирование матрицы. Это переход от матрицы А к матрице , в которой строки и столбцы поменялись местами с сохранением порядка. Матрица- транспонированная относительно А.

Например:

;

Свойства операции транспонирования:

1) ; 2)3)4)