Тема 10. Элементы физической кинетики

Наука, изучающая процессы, возникающие при нарушениях равновесия, носит название физической кинетики. Нарушение равновесия сопровождается переносом массы (диффузия), импульса (внутреннее трение) или энергии (теплопроводность). Эти процессы называютсяявлениями переноса. Они возникают самопроизвольно вследствие теплового движения при отклонении вещества от равновесного состояния и являются необратимыми.

Явления переноса протекают медленно, несмотря на то, что все они происходят благодаря быстрому движению молекул. Свободному движению молекул препятствуют их взаимные столкновения. Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом. Под столкновением молекул подразумевается процесс взаимодействия между молекулами, в результате которого молекулы изменяют направление своего движения. Столкновения молекул представляют как раз тот механизм, который приводит систему в равновесное состояние. В идеальном газе эти столкновения происходят только между двумя молекулами, а одновременными столкновениями между тремя и большим числом молекул можно пренебречь.

Расстояние, которое проходит молекула между двумя последовательными столкновениями, называется длиной свободного пробега молекулы. Так как молекул в газе чрезвычайно много, то вводят понятие средней длины свободного пробега молекул. Средней длиной свободного пробега молекул называется среднее расстояние, которое молекула проходит без столкновений.

Эффективный диаметрмолекулы – минимальное расстояние, на которое сближаются центры двух молекул при столкновении.

Число столкновений, испытываемых молекулой в единицу времени, может быть различным. Поэтому следует говорить о среднем значении этой величины.

Средняя длина свободного пробега и среднее число столкновений в единицу времениz являются главными характеристиками процесса столкновений газовых молекул. Эти величины связаны между собой:=, гдеv - средняя арифметическая скорость.

Можно показать, что z =.

При постоянной температуре концентрация газа пропорциональна его давлению (р=nkT) и средняя длина свободного пробега молекул:=. (2)

С уменьшением давления длина свободного пробега молекул возрастает в той же мере, в какой падает давление. (1/р). При определенном значении давления она станет равной размерам сосуда.

Диффузия.

Диффузияесть процесс проникновения одного газа в объем, занятый другим газом, или же движение газа из области повышенной концентрации в область, где концентрация ниже (самодиффузия).

Если газ предоставлен самому себе, то в результате диффузии происходит постепенное выравнивание концентраций. Если же неравновесное состояние поддерживается неизменным, то устанавливается стационарный (не зависящий от времени) процесс. Рассмотрение его проще нестационарного.

Пусть в большом сосуде с плоскими стенками 1, 2 поддерживается разность концентраций газа n₁и n₂(рис.36.1). Выберем мысленно произвольную плоскостьx =const и на ней элементарную площадкуS. Оценим число молекул, диффундирующих черезdS. Построим элементарный параллелепипед высотойdx ==vdt. Внутри этого параллелепипеда молекулы не испытывают соударений. Следовательно, одна шестая всех заключенных в нижнем объемеdtпройдет за времяdtчерезS. В то же время пройдут молекулы и из верхнего объема: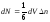. Величинуопределим из условия:. Воспользуемся известным разложением:

, ,

где – модуль градиента концентрации (градиент концентрации – вектор, направленный в сторону возрастания концентрации). Взяв разность, получим:.

Разность числа прошедших молекул равна:

(1)

Задолго до появления молекулярно-кинетических представлений Фиком был эмпирически установлен закон диффузии:

, (2)

где D– коэффициент диффузии.

Из полученного с помощью кинетической теории соотношения (1) и закона Фика (2) коэффициент диффузии: ([D]=м²/с).

Умножим обе части (2) на массу одной молекулы m₀и учтем, что=nm₀- плотность компонента переносимого газа, dm=n₀dN - переносимая масса газа:.

Отсюда сформулируем физический смысл коэффициента диффузии: это масса, переносимая в единицу времени через единичную площадку в направлении нормали к этой площадке в сторону убывания плотности компонента при градиенте плотности, равном единице. [D]=м² с.

Вязкость (внутреннее трение).

При движении соседних слоев газа с различными скоростями между ними возникает сопротивление перемещению, или т.н. силы внутреннего трения. Причиной этого явления, называемого вязкостью (или внутренним трением), является наложение упорядоченного движения слоев газа с различными скоростями и теплового хаотического движения молекул со скоростями, зависящими от температуры. При этом происходитперенос импульса упорядоченного движения молекул из одного слоя в другой. Еще Ньютон показал, что при небольших скоростях течения сила внутреннего трения между слоями, рассчитанная для элементарной площадки S:, (1)

где u-скорость упорядоченного движения,–градиент скорости (вектор, направленный в сторону возрастания скорости),– коэффициент пропорциональности, названный коэффициентом внутреннего трения (коэффициентом вязкости). Он численно равен импульсу, переносимому в единицу времени через единичную площадку при единичном градиенте скорости. С помощью элементарной кинетической теорией можно рассчитать:[ ]=Па с

Зависимость коэффициента вязкости от внешних параметров:   n  p/T,1/nТ/р;v .

Теплопроводность – это выравнивание температуры за счет переноса молекулами энергии между частями вещества, которые первоначально имели различную температуру. Причина этого явления в том, что хаотическое тепловое движение молекул газа, имеющих различные скорости, а, следовательно, и различные средние кинетические энергии, приводит кнаправленному переносу энергиив форме теплоты. Количество теплоты, переносимое через элементарную площадку в направлении нормали к этой площадке, выражается законом Фурье:

, (2)

где Т– абсолютная температура,– градиент температуры (вектор, направленный в сторону убывания температуры),- коэффициент теплопроводности, численно равный количеству теплоты. переносимому в единицу времени через единичную площадку при единичном градиенте температуры. С помощью молекулярно-кинетической теорией можно рассчитать:. [ ]=Вт/м К

Связь коэффициентов вязкости, теплопроводности и диффузии: = D, =c_V= c_V D

Так как  , c_V~1/m₀ ,то ~.

 не зависит от давления. При известных c_V и по одному из коэффициентов находят остальные.

Итак, по известным коэффициентам переноса можно найти важнейшие характеристики газа - длину свободного пробега молекул и эффективный их диаметр.