Тема 30. Элементы квантовой механики

Французский ученый Луи де Бройль, развивая представления о двойственной корпускулярно-волновой природе света, выдвинул в 1923 году гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что между свойствами света и свойствами материальных частиц существует глубокая аналогия, следовательно материальные частицы обладают также двойственной природой, т.е. в определенных условиях проявляются их волновые свойства.

Де-Бройль постулировал, что частице с импульсом соответствует длина волны:(1.2)

Это соотношение (формула де Бройля) справедливо для любой частицы с импульсом р.

Вскоре гипотеза де Бройля была подтверждена экспериментально. Американские физики К.Дэвиссон и Л.Джермер в 1927 г. изучали рассеяние электронов на монокристалле никеля с помощью установки, изображенной на рис. Пучок электронов из электронной пушки 1 направлялся на кристалл никеля 2, рассеянные от кристалла электроны 3 улавливались специальным приемником 4, соединенным с чувствительным гальванометром. Интенсивность отраженного пучка определялась по силе тока, текущего через гальванометр. Опыты показали, что при заданном угле падения электроны отражаются от поверхности кристалла под различными углами, причем в одних направлениях наблюдаются максимумы числа отраженных электронов, в других – минимумы, то есть наблюдалась дифракционная картина. Это явление наблюдалось, когда длина электронной волны де Бройля 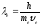имеет порядок межатомного расстояния в кристалле. Дифракционные максимумы соответствовали формуле Вульфа-Брэггов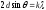, а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (1.2).

Позже П.С.Тартаковский и Г.Томсон исследовали прохождение быстрых электронов через тонкие металлические пленки. При этом на фотопластинках за этими пленками получалась дифракционная картина такая же, как при дифракции рентгеновских лучей на поликристаллах.

В 1849 г. В.А.Фабрикант, Л.М.Биберман и Н.Г.Сушкин осуществили опыты по дифракции электронов с очень малой силой тока в приборе, то есть каждый электрон регистрировался фотопластинкой в случайных местах. При длительной экспозиции была получена такая же дифракционная картина, как и при короткой с большой силой тока. Это означает, что волновые свойства присущи каждому электрону в отдельности, однако дифракция одного электрона не дает всей системы точек, которая получается при дифракции от потока. След одного электрона окажется лишь в одной точке, которая разрешена условием дифракции. В этом проявляется корпускулярная природа электронов, так как электрон не может расплыться. В какое именно из мест попадет электрон, говорить нельзя. Можно говорить лишь о вероятности попадания в точку пространства.

Таким образом, электрону присуща двойственная природа, т.е. он сочетает в себе свойства и частицы, и волны. Волновая природа электронов подтверждается опытами по их дифракции. Корпускулярная природа электронов проявляется в том, что электрон действует как единое целое, не дробясь на части.

Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рассчитываемой по формуле де Бройля (1.2).

Соотношениенеопределенностей Гейзенберга.

Подтвержденная экспериментально гипотеза де Бройля о корпускулярно-волновом дуализме свойств вещества коренным образом изменила представления о свойствах микрообъектов. Всем микрообъектам присущи и корпускулярные, и волновые свойства; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в классическом понимании.

В.Гейзенберг, учитывая волновые свойства микрочастиц и связанные с волновыми свойствами ограничения в их поведении, пришел в 1927 г. к выводу, что объект микромира невозможно одновременно с любой наперед заданной точностью харак­теризовать и координатой и импульсом. Согласно соотношению неопределенностей Гейзенберга,микрочастица не может иметь одновременно и определен­ную координату (х,у, z),и определенную соответствующую проекцию импульса (р_х,р_у, p_z),причем неопределенности этих величин удовлетворяют условиям:,,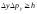, 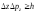(2.1)

где x,у,z– неопределенности координат частицы, а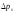,,- неопределенность компоненты импульса. Произведение неопределенностей координаты и соответствующей ей проекции импульса не может быть меньше величины порядкаh. То есть, чем точнее мы знаем координату, тем менее определена проекция импульса и наоборот. Отсюда вытекает и фактическая невозможность одновременно с любой, наперед заданной точностью измерить координату и импульс микрообъекта.

Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличия у нее волновых свойств. Оно является квантовым ограничением применимости классической механики к микрообъектам и позво­ляет оценить, например, в какой мере можно применять понятия классической меха­ники к микрочастицам, в частности, с какой степенью точности можно говорить о траекториях микрочастиц. Известно, что движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Выразим соотношение неопределенностей (2.1) в виде

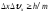(2.4)

Из этого выражения следует, что чем больше масса частицы, тем меньше неопределен­ности ее координаты и скорости и, следовательно, с тем большей точностью можно применять к этой частице понятие траектории. Для описания движения макротел с абсолютной достоверностью можно пользоваться законами классической механики, чего нельзя делать для описания, например, движе­ния электрона в атоме.

В квантовой теории рассматривается также соотношение неопределенностей для энергии Еи времениt, т.е. неопределенности этих величин удовлетворяют условию

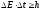(4.5)

где DЕ– неопределенность энергии некоторого состояния системы,Dt– промежуток времени, в течение которого оно существует. Следовательно, систе­ма, имеющая среднее время жизниDt, не может быть охарактеризована определенным значением энергии; разброс энергииDЕ=h/Dtвозрастает с уменьшением среднего времени жизни.

Волновая функция и ее физический смысл.

Состояние частицы в квантовой механике описывают волновой функцией, которая зависит от координат и времени(x,y,z,t). Конкретный вид-функции определяется состоянием частицы, характером действующих на нее сил. Если силовое поле, действующее на частицу, является стационарным, т.е. не завися­щим от времени, то-функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой – от координат:

(3.1)

В дальнейшем будем рассматривать только стационарные состояния. -функция является вероятностной характеристикой состояния частицы. Чтобы пояснить это, мысленно выделим достаточно малый объем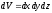, в пределах которого значения-функции будем считать одинаковыми. Тогда вероятность нахожденияdW частицы в данном объ­еме пропорциональна ему и зависит от квадрата модуля-функции (квадрата модуля амплитуды волн де Бройля):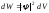(3.2)

Отсюда следует физический смысл волновой функции:

. (3.3)

Квадрат модуля волновой функции имеет смысл плотности вероят­ности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z.

Интегрируя выражение (3.2) по объему, определяем вероятность нахождения частицы в этом объеме в условиях стационарного поля:

(3.4)

Если известно, что частица находится в пределах объема V, то инте­грал выражения (3.4), взятый по объемуV, должен быть равен единице:

(3.5)

– условие нормировки -функции.

Уравнение Шредингера.

Основной характеристикой состояния атомов, молекул, элементарных частиц является -функция. Аналитическое выражение-функции в каждом конкретном случае можно получить путем решения волнового уравнения – основного урав­нения квантовой механики, предложенного Э.Шредингерам в 1920 г.

Применительно к стационарным состояниям уравнение Шредингера имеет вид:

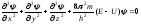. (4.1)

где т – масса частицы;Е иU – ее полная и потенциальная энергии.

Если частица перемещается только вдоль некоторой линии, например, вдоль оси ОХ (одномерный случай), то уравнение Шрёдингера упрощается и принимает вид:

(4.2)

Одним из наиболее простых примеров использования уравнения Шрёдингера является решение задачи о движении частицы в одномерной потенциальной яме.

Пусть электрон перемещается вдоль оси ОХ только в пределах 0<х<l (рис.4.1). Это означает, чтовуказанном интервале-функция отлична от нуля,авне интервала(х < 0,х l) равна нулю.

Так как на частицу в выделенном интервале силовые поля не действуют, то ее потенциальная энергия может иметь любое постоянное значение (наиболее удобно принять U=0). Вне этого интервала электрона нет, поэтому следует считать его потенциальную энергию бесконечно большой. На рис. 4.1 показана графическая зависимостьU=f(x). Интервал 0<х<l, удовлетворяющий сформулиро­ванным выше условиям, называютодномерной прямоугольной потенциальной ямой с бесконечно высокими стенками. С учетомU=0 уравнение Шрёдингера (4.2) для интервала 0<х<l имеет вид:

. (4.3)

Введем обозначение: 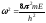, (4.4)

тогда: (4.5)

Это уравнение аналогично дифференциальному уравнению гармонического колебания, решение которого:

, (4.10)

где –амплитуда волновой функции,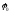–ее начальная фаза. Чтобы найти две постоянные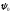и, а также возможные значенияилиЕ, рассмотрим граничные условия:

1) при х =0= 0. Подставляя эти значения в (4.10), получаем

Физический смысл здесь имеет только одно значение: 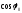= 0, откуда.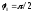

2) при х =l= 0.Cучетомиз (4.10) имеем:

Физический смысл здесь имеет только одно значение:

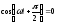, или 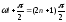, откуда

, (4.7)

где п – целое число, оно принимает значения 1, 2, 3, ...;п ≠ 0, так как в противном случае= 0 при любомх, что означает отсутствие электрона в потенциальной яме. Числоnназываютквантовым числом. Из (4.4) находим энергию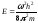, что с учетом (4.7) дает:

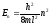. (4.8)

Индекс nпри Е показывает, что различным значениям квантового числаnсоответствует и разная энергия.

Подставляя (4.7) в (4.5) и учитывая, получаем

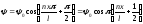. (4.9)

Из (4.8) следует, что решение уравнения Шредингера для электрона в потенциальной яме без каких-либо дополнительных постулатов приводит к дискретным, квантованным значениям энергии: 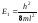;и т.д.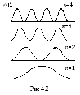

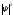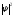Возведя (4.9) в квадрат, получим плотность вероятности нахождения электрона в разных точках потенциальной ямы. На рис.4.2. показана графическая зависимостьотхпри разных дискретных состояниях, то есть разных квантовых числах. Как видно из рисунка, электрон может с разной с разной вероятностью находиться в разных местах потенциальной ямы. Есть такие точки, в которых вероятность нахождения электрона вообще равна нулю. Это существенно отличается от представлений классической физики, согласно которым равновероятно нахождение частицы в раз­ных местах потенциальной ямы