Тема 19. Затухающие и вынужденные колебания. Сложение колебаний

Реально свободные колебания под действием сил сопротивления всегда затухают. Объясняется это действием сил, тормозящих движение, например, сил трения в месте подвеса при колебаниях маятника, или силой сопротивления среды. В этом случае энергия механических колебаний постепенно расходуется на работу против этих сил. Поэтому свободные колебания под действием сил сопротивления всегда затухают.

Пусть точка совершает линейное гармоническое колебание в вязкой среде. Из опыта известно, что сила сопротивления среды зависит от скорости и направлена в сторону, противоположную скорости. При малых скоростях: , гдеr– постоянная величина, называемая коэффициентом сопротивления среды. Уравнение колебаний:.

Введем обозначе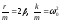ния:, тогда дифференциальное уравнение затухающего колебания:

(1)

где 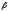– коэффициент затухания,₀– собственная частота колебания. При отсутствии трения=0, уравнение примет вид уравнения для свободных незатухающих колебаний. В результате решения уравнения (1) получим зависимость смещения х от времени, то есть уравнение затухающего колебательного движения:(2)

Выражение 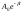называется амплитудой затухающего колебания. Амплитуда уменьшается с течением времени и тем быстрее, чем больше коэффициент затухания. Огибающая на графике зависит от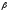. Чем она больше, тем круче огибающая, то есть колебания быстрее затухают (рис.24.1).

Путем подстановки функции (2) и ее производных по времени в уравнение (1), можно найти значение угловой частоты: . Период затухающих колебаний равен:.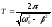

Наглядной характеристикой затухания является отношение значений двух амплитуд, соответствующих промежутку времени в один период. Это отношение называют декрементом затухания :.

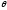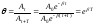Его натуральный логарифм есть безразмерная величина, называемая логарифмическим декрементом затухания: .

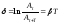Промежуток времени , в течение которого амплитуда затухающего колебания убывает вераз, называютвременем релаксации.

Тогда выражение для логарифмического декремента затухания примет вид: 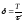или.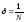

Логарифмический декремент затухания– величина, обратная числу колебаний N, по истечении которых амплитуда колебаний уменьшается вераз.

Вынужденные колебания. Резонанс.

Колебания системы, которые совершаются за счет работы периодически меняющейся внешней силы, называются вынужденными.

Пусть на систему действует внешняя сила, меняющаяся со временем по гармоническому закону: 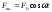, гдеF₀– амплитуда силы (максимальное значение),– угловая частота колебаний вынуждающей силы. Тогда уравнение движения будет иметь вид:=.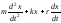

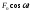Разделим обе части этого уравнения на m и введем вновь обозначения: , тогда получим неоднородное дифференциальное уравнение второго порядка:=(1)

Решение этого уравнения, как известно из высшей математики, представляет собой сумму свободных и вынужденных колебаний:

Таким образом, вынуждающая сила раскачивает систему, сообщая ей запас энергии, и пополняет расходуемую энергию, поддерживая колебательное движение. В первый момент система совершает помимо вынужденных еще свободные колебания. Частота свободных колебаний определяется по известной формуле: 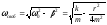. Эти колебания затухают, и устанавливаются колебания, частота которых равна частоте вынуждающей силы, то есть вынужденные колебания. Когда работа вынуждающей силы сравнивается с энергией потерь, колебания становятсяустановившимися. Амплитуда этих колебаний должна быть постоянной, если постоянна амплитуда вынуждающей силы.

Решение дифференциального уравнения при установившемся движении имеет вид: 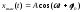(2)

где А, – величины, которые требуется определить,– круговая частота колебаний внешней переменной силы. Подставляя (2) в (1) , получаем искомые величины:

(3) (4)

Амплитуда колебаний зависит от амплитуды и частоты внешних сил. При некоторой частоте внешних сил знаменатель в выражении (3) будет иметь минимальное значение, а амплитуда вынужденных колебаний – максимальное значение. Эта частота называется резонансной. Для ее нахождения, приравниваем к нулю производную: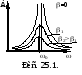

,

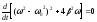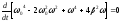
Сократим на 4: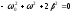, откуда получим:.

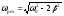Резонансная амплитуда:

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте ₀, называетсярезонансом.

При коэффициенте затухания =0, когда отсутствуют силы сопротивления,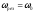, аА_резстановится бесконечно большой. На рисунке 25.1. даны зависимости амплитуды колебаний от частоты вынуждающей силы. Отдельные кривые соответствуют различным значениям коэффициента затухания. Эти кривые называются резонансными. Чем меньше коэффициент затухания, тем резче изменяется амплитуда вынужденных колебаний. При резонансе наступают наиболее благоприятные условия для поступления энергии в колеблющуюся систему от источника внешней силы. Увеличение амплитуды происходит до тех пор, пока вся работа внешней силы не сравняется с энергией потерь.