Тема 20. Волны. Уравнение волны. Энергия волны
Процесс распространения колебаний в среде называется волновымпроцессом (иливолной). Все разнообразие волн в природе и технике подразделяют на два типа: волны механические (упругие) и электромагнитные.
Упругими(илимеханическими) волнами называются механические возмущения, распространяющимися в упругой среде.
Упругие волны бывают продольные и поперечные. В продольныхволнах частицы среды колеблются в направлении распространения волны, впоперечных– в плоскостях, перпендикулярных направлению распространения. Поперечные волны возникают при деформациях сдвига.
Скорость
распространения продольных волн в
тонком стержне
,
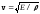где Е – модуль Юнга,– плотность среды.
Скорость
распространения поперечных волн в
изотропном твердом теле
,
где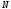
– модуль сдвига.
Скорость
распространения продольных (звуковых)
волн в жидкости и в газе
,
где К – модуль объемной упругости среды,– плотность среды.
Например, в воздухе: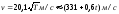
,
где Т – термодинамическая температура,
измеренная по шкале Кельвина, t –
температура, измеренная по шкале Цельсия.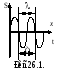
При распространении колебаний в среде частицы не перемешаются вместе с волной, а лишь колеблются около своих положений равновесия. Поступательно перемещаются лишь фаза и энергия колебаний.
Графически волну изображают так же, как и колебания (рис.26.1).
Геометрическое место точек, колеблющихся в одинаковых фазах, называется волновой поверхностью. В зависимости от формы волновой поверхности различают сферические, плоские, цилиндрические волны. Геометрическое место точек, до которых доходят колебания с одинаковой фазой к некоторому моменту времениt, называетсяфронтом волны.Фронт волны является частным случаем волновой поверхности.
Пусть плоская волна распространяется вдоль оси х (рис.26.1). Эта волна характеризуется: длиной волны, периодом, амплитудой, частотой, фазовой скоростью.
Расстояние, на которое определенная фаза распространяется за один период колебания, называется длиной волны. Из рисунка видно, что– это наименьшее расстояние между точками, колеблющимися в одинаковых фазах. Скорость распространения волны - фазовая скорость.Фазовая скорость– равна скорости перемещения в пространстве точек поверхности, соответствующей любому фиксированному значению фазы.
.
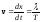Волна, распространяющаяся в пространстве от какого-либо источника, называется бегущей волной.
Уравнением волны
называется алгебраическое выражение,
которое дает зависимость смещения
колеблющейся точки s как функция ее
координат (х) и времени t:
.
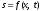В общем случае
уравнение плоской волны, распространяющейся
вдоль положительного направления оси
0Х, имеет вид:
,
(2)
где
– начальная фаза колебаний;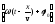
–
фаза плоской бегущей волны.
Для характеристики волн используется волновое число k, характеризующее скорость изменения фазы в пространстве
.
(3)
Учитывая (3),
уравнение (2) примет вид:
(4)
Уравнение волны, распространяющейся вдоль отрицательного направления оси 0Х, отличается от (4) знаком члена kx.
Из условия
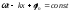получаем выражение для фазовой скорости:
.