Тема 17. Основы теории Максвелла для электромагнитного поля. Электромагнитные волны

В 60-х гг. XIXв. английский ученый Дж. Максвелл (1831-1879) обобщил экспериментально установленные законы электрического и магнитного полей и создал законченную единуютеорию электромагнитного поля. Она позволяет решитьосновную задачу электродинамики: найти характеристики электромагнитного поля заданной системы электрических зарядов и токов.

Максвелл выдвинул гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле , циркуляция которого и является причиной возникновения ЭДС электромагнитной индукции в контуре:

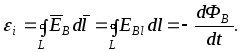(5.1)

Уравнение (5.1) называют вторым уравнением Максвелла. Смысл этого уравнения заключается в том, что изменяющееся магнитное поле порождает вихревое электрическое, а последнее в свою очередь вызывает в окружающем диэлектрике или вакууме изменяющееся магнитное поле. Поскольку магнитное поле создается электрическим током, то, согласно Максвеллу, вихревое электрическое поле следует рассматривать как некоторый ток, который протекает как в диэлектрике, так и в вакууме. Максвелл назвал этот токтоком смещения.

Ток смещения, как это следует из теории Максвелла и опытов Эйхенвальда, создает такое же магнитное поле, как и ток проводимости.

В своей теории Максвелл ввел понятие полного тока, равного сумме токов проводимости и смещения. Следовательно, плотность полного тока

По Максвеллу полный ток в цепи всегда замкнут, то есть на концах проводников обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.

Введя понятие полного тока, Максвелл обобщил теорему о циркуляции вектора (или):

(5.6)

Уравнение (5.6) называется первым уравнением Максвелла в интегральной форме. Оно представляет собой обобщенный закон полного тока и выражает основное положение электромагнитной теории:токи смещения создают такие же магнитные поля, как и токи проводимости.

Созданная Максвеллом единая макроскопическая теория электромагнитного поля позволила с единой точки зрения не только объяснить электрические и магнитные явления, но предсказать новые, существование которых было впоследствии подтверждено на практике (например, открытие электромагнитных волн).

Обобщая рассмотренные выше положения, приведем уравнения, составляющие основу электромагнитной теории Максвелла.

1. Теорема о циркуляции вектора напряженности магнитного поля:

Это уравнение показывает, что магнитные поля могут создаваться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.

2. Электрическое поле может быть как потенциальным (), так и вихревым (), поэтому напряженность суммарного поля. Так как циркуляция вектораравна нулю, то циркуляция вектора напряженности суммарного электрического поля

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и меняющиеся во времени магнитные поля.

3. ,

4.

где – объемная плотность заряда внутри замкнутой поверхности;– удельная проводимость вещества.

Для стационарных полей (E=const, B=const) уравнения Максвелла принимают вид

то есть источниками магнитного поля в данном случае являются только токи проводимости, а источниками электрического поля – только электрические заряды. В этом частном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянныеэлектрические и магнитные поля.

Используя известные из векторного анализа теоремы Стокса и Гаусса, можно представитьполную систему уравнений Максвелла в дифференциальной форме(характеризующих поле в каждой точке пространства):

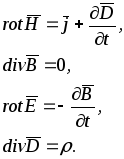(5.7)

Очевидно, что уравнения Максвелла не симметричныотносительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме ту же роль, что и законы Ньютона в механике.

Электромагнитной волнойназывают переменное электромагнитное поле, распространяющееся в пространстве с конечной скоростью.

Существование электромагнитных волн вытекает из уравнений Максвелла, сформулированных в 1865 г. на основе обобщения эмпирических законов электрических и магнитных явлений. Электромагнитная волна образуется вследствие взаимной связи переменных электрического и магнитного полей – изменение одного поля приводит к изменению другого, то есть чем быстрее меняется во времени индукция магнитного поля, тем больше напряженностьэлектрического поля, и наоборот. Таким образом, для образования интенсивных электромагнитных волн необходимо возбудить электромагнитные колебания достаточно высокой частоты.Фазовая скоростьэлектромагнитных волн определяется электрическими и магнитными свойствами среды:

В вакууме () скорость распространения электромагнитных волн совпадает со скоростью света; в веществе, поэтомускорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.

Электромагнитные волны являются поперечными волнами– колебания векторовипроисходят во взаимно перпендикулярных плоскостях, причем векторы,иобразуют правовинтовую систему. Из уравнений Максвелла также следует, что в электромагнитной волне векторыивсегда колеблются в одинаковых фазах, а мгновенные значенияЕиНв любой точке связаны соотношением

Уравнения плоской электромагнитной волны в векторной форме:

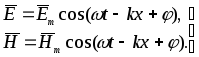(6.66)

На рис. 6.21 показан «моментальный снимок» плоской электромагнитной волны. Из него видно, что векторы иобразуют с направлением распространения волны правовинтовую систему. В фиксированной точке пространства векторы напряженности электрического и магнитного полей изменяются со временем по гармоническому закону.

Для характеристики переноса энергии любой волной в физике введена векторная величина, называемая плотностью потока энергии. Она численно равна количеству энергии, переносимой в единицу времени через единичную площадку, перпендикулярную к направлению, в котором распространяется волна. Направление векторасовпадает с направлением переноса энергии. Величину плотности потока энергии можно получить, умножив плотность энергиина скорость волны

Плотность энергии электромагнитного поля слагается из плотности энергии электрического поля и плотности энергии магнитного поля:

или

(6.67)

Умножив плотность энергии электромагнитной волны на ее фазовую скорость, получим плотность потока энергии

(6.68)

Векторы ивзаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему. Поэтому направление векторасовпадает с направлением переноса энергии, а модуль этого вектора определяется соотношением (6.68). Следовательно, вектор плотности потока энергии электромагнитной волны можно представить как векторное произведение

(6.69)

Вектор называютвектором Умова-Пойнтинга.