Тема 13. Постоянный электрический ток

Электрическим токомназывают упорядоченное движение заряженных частиц или заряженных макроскопических тел. Различают два вида электрических токов – токи проводимости и конвекционные токи.

Током проводимостиназывают упорядоченное движение в веществе или вакууме свободных заряженных частиц – электронов проводимости (в металлах), положительных и отрицательных ионов (в электролитах), электронов и положительных ионов (в газах), электронов проводимости и дырок (в полупроводниках), пучков электронов (в вакууме). Этот ток обусловлен тем, что в проводнике под действием приложенного электрического поля напряженностьюпроисходит перемещение свободных электрических зарядов (рис. 2.1,а).

Конвекционным электрическим токомназывают ток, обусловленный перемещением в пространстве заряженного макроскопического тела (рис. 2.1, б).

Для возникновения и поддержания электрического тока проводимости необходимы следующие условия:

1) наличие свободных носителей тока (свободных зарядов);

2) наличие электрического поля, создающего упорядоченное движение свободных зарядов;

3) на свободные заряды, помимо кулоновских сил, должны действовать сторонние силынеэлектрической природы; эти силы создаются различнымиисточниками тока(гальваническими элементами, аккумуляторами, электрическими генераторами и др.);

4) цепь электрического тока должна быть замкнутой.

За направление электрического тока условно принимают направление движения положительных зарядов, образующих этот ток.

Количественной меройэлектрического тока являетсясила тока I– скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечениеS проводника в единицу времени:

(2.1)

Ток, сила и направление которого не изменяются с течением времени, называется постоянным(рис. 2.2, а). Для постоянного тока

Электрический ток, изменяющийся с течением времени, называется переменным. Примером такого тока является синусоидальный электрический ток, применяемый в электротехнике и электроэнергетике (рис. 2.2, б).

Единица силы тока – ампер(А). В СИ определение единицы силы тока формулируется следующим образом: 1 А – это сила такого постоянного тока, который при протекании по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, создает между этими проводниками силу, равнуюна каждый метр длины.

Для характеристики направления электрического тока проводимости в разных точках поверхности проводника и распределения силы тока по этой поверхности вводится плотность тока.

Плотностью тока называют векторную физическую величину, совпадающую с направлением тока в рассматриваемой точке и численно равную отношению силы токаdI, проходящего через элементарную поверхность, перпендикулярной направлению тока, к площади этой поверхности:

(2.2)

Единица плотности тока – ампер на квадратный метр(А/м²).

Плотность постоянного электрического тока одинакова по всему поперечному сечению однородного проводника. Поэтому для постоянного тока в однородном проводнике с площадью поперечного сечения Sсила тока равна

Если в цепи на носители тока действуют только силы электростатического поля, то происходит перемещение зарядов от точек с большим потенциалом к точкам с меньшим потенциалом. Это приводит к выравниванию потенциалов во всех точках цепи и к исчезновению тока. Поэтому для поддержания постоянного электрического тока в цепи необходимо наличие устройства, способного создавать и поддерживать разность потенциалов за счет работы некоторых сторонних сил. Такие устройства называют источниками тока.

Под действием сторонних сил носители тока движутся внутри источника электрической энергии против сил электростатического поля (против кулоновских сил, вызывающих соединение разноименных зарядов, а, следовательно, выравнивание потенциалов и исчезновение тока), так что на концах внешней цепи поддерживается постоянная разность потенциалов и в цепи протекает постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой сторонних сил при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС) источника:

(2.3)

Единица ЭДС – вольт(В).

Сторонняя сила, действующая на заряд , может быть выражена через напряженностьполя сторонних сил

Тогда работа сторонних сил по перемещению заряда на замкнутом участке цепи будет равна

(2.4)

Разделив (2.4) на и учитывая (2.3), получим выражение для ЭДС, действующей в цепи,

то есть ЭДС, действующая в замкнутой цепи, есть циркуляция вектора напряженности поля сторонних сил. Как частный случай, ЭДС на участке 1-2 цепи равна

(2.5)

На заряд помимо сторонних сил действуют также силы электростатического поля (кулоновские силы)Таким образом, результирующая сила, действующая в цепи на заряд, определяется следующим образом:

Тогда работа, совершаемая этой силой над зарядом на участке 1-2 цепи, равна

Используя выражение (2.5) и ранее полученное соотношение 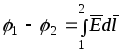, можем записать

(2.6)

Для замкнутой цепи работа электростатических сил равна нулю, поэтому в такой цепи

Разделив (2.6) на , получим

(2.7)

то есть напряжением на участке цепи называется физическая величина, определяемая работой, совершаемой суммарным полем кулоновских и сторонних сил при перемещении единичного положительного заряда.

Таким образом, напряжение является более широким понятием, чем разность потенциалов: напряжение на участке цепи равно разности потенциалов только в том случае, если на этом участке не действует ЭДС, то есть сторонними силами не совершается работа. Такой участок электрической цепи называется однородным.

Немецкий физик Г. Ом (1787-1854) экспериментально установил, что сила тока в однородном проводнике пропорциональна разности потенциалов на его концах и обратно пропорциональна сопротивлению проводника (закон Ома для участка цепи):

(2.8)

где R–электрическое сопротивлениепроводника, определяющее упорядоченность перемещения свободных носителей тока.

Электрическое сопротивление металлического проводника обусловлено тем, что свободные электроны при своем движении взаимодействуют (соударяются) с положительными ионами кристаллической решетки. Поэтому сопротивление проводников зависит, прежде всего, от материала проводника, то есть строения его кристаллической решетки. Для однородного цилиндрического проводника длиной lи площадью поперечного сеченияSсопротивление определяется по формуле

(2.9)

где удельное сопротивление(сопротивление однородного цилиндрического проводника, имеющего единичную длину и единичную площадь поперечного сечения), характеризующее материал проводника.

Единица сопротивления – ом: 1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток силой 1 А.

Величина обратная сопротивлению, называетсяэлектрической проводимостью. Единица проводимости –сименс: 1 См – электрическая проводимость проводника сопротивлением 1 Ом.

Удельное электрическое сопротивление проводника зависит не только от рода вещества, но и от температуры:

(2.10)

где удельное сопротивление при 0^оС;t– температура (по шкале Цельсия);температурный коэффициент сопротивления, характеризующий относительное изменение сопротивления проводника при его нагревании на 1^о С или 1 К:

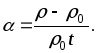
Температурные коэффициенты сопротивления веществ различны при разных температурах. Однако для многих металлов изменение с температурой невелико. Для всех чистых металлов

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (2.9) в закон Ома (2.8), получим

или

где величина называетсяудельной проводимостью(См/м). Учитывая, чтонапряженность электрического поля в проводнике, аплотность тока, последнее выражение можно записать в следующем виде:

Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора , то направленияисовпадают. Поэтому, в окончательном виде

(2.11)

Выражение (2.11) представляет собой закон Ома в дифференциальной форме, который связывает плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

Последовательное и параллельное соединение проводников. Электрическая цепь представляет собой совокупность различных проводников и источников тока. В общем случае цепь является разветвленной и содержит участки, где проводники могут соединяться последовательно и параллельно.

При последовательном соединении проводников(рис. 2.3, а):

а) сила тока во всех частях цепи одинакова (I =const);

б) напряжение на зажимах цепи равно сумме падений напряжений на отдельных участках ().

Учитывая эти положения и используя закон Ома для однородного участка, найдем общее (эквивалентное) сопротивление цепи:

Или (2.12)

Таким образом, общее сопротивление цепи, состоящей из последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников.

Рис. 2.3

При параллельном соединении проводников(рис. 2.3, б):

а) сила тока в неразветвленной части цепи равна сумме сил токов, протекающих в разветвленных участках цепи ();

б) падения напряжения в параллельно соединенных участках цепи одинаковы и равны напряжению на зажимах цепи ().

С учетом этих положений и на основании закона Ома для однородного участка цепи найдем общее (эквивалентное) сопротивление цепи:

или

(2.13)

Таким образом, при параллельном соединении проводников складываются величины, обратные сопротивлениям отдельных участков цепи (проводимости ветвей).

Работа и мощность тока. Закон Джоуля-Ленца

Рассмотрим однородный проводник, по концам которого приложено напряжение . За времяdtчерез поперечное сечение проводника переносится заряд. Так как ток представляет собой перемещение зарядаdqпод действием электрического поля, работа тока есть

(2.14)

Используя закон Ома для однородного участка цепи, формулу (2.14) можно представить в виде 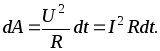(2.15)

Мощность электрического тока– это быстрота совершения работы, то есть(2.16)

Единица мощности – ватт: 1 Вт – мощность, выделяемая в проводнике за 1 с при протекании тока силой 1 А.

Если ток протекает по неподвижному металлическому проводнику, то вся работа тока затрачивается на его нагревание и по закону сохранения энергии

Таким образом, с учетом (2.14) и (2.15) получим

(2.17)

Количество теплоты, выделяющееся за конечный промежуток времени от 0 до tпри прохождении постоянного тока силойI найдем, интегрируя выражение (2.17):(2.18)

Таким образом, количество теплоты, которое выделяется в проводнике с током, пропорционально квадрату силы тока, времени его протекания и сопротивлению проводника.Выражение (2.18) есть закон Джоуля-Ленца для участка цепи постоянного тока. Он был установлен экспериментально Д. Джоулем (1841) и независимо от него Э.Х. Ленцем (1842).

Выделим в проводнике элементарный цилиндрический объем (ось цилиндра совпадает с направлением тока). Сопротивление этого элементарного объемаТогда по закону Джоуля-Ленца за времяdtв этом объеме выделится теплота

Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью электрического тока:

Используя дифференциальную форму закона Ома (2.11) и соотношение , получим

(2.19)

Формула (2.19) является обобщенным выражением закона Джоуля-Ленца в дифференциальной форме, пригодным для любого проводника.

Закон Ома в интегральной форме

Для однородного участка цепи, то есть для участка, на котором не действуют сторонние силы, закон Ома записывается в форме (2.8). Рассмотрим теперь неоднородныйучасток цепи 1-2 (рис. 2.8), где действует ЭДС источникаи на концах которого приложена разность потенциалов.

На рассматриваемом участке работа всех приложенных сил (сторонних и электростатических), совершаемая над носителями тока, согласно (2.6) равна:

В этой формуле ЭДС берется либо с положительным, либо с отрицательным знаком. Если ЭДС способствует движению положительных зарядов в направлении обхода (в направлении 1-2), то есть внутри источника обход совпадает с перемещением зарядов от катода к аноду, то(рис. 2.8, а). Если ЭДС препятствует движению положительных зарядов в направлении обхода, то(рис. 2.8, б).

По закону сохранения и превращения энергии работа равна теплоте, выделяющейся на участке 1-2 за времяt(эта теплота определяется согласно закону Джоуля-Ленца):

(2.20)

Приравнивая (2.6) и (2.20), получим

(2.21)

или

(2.22)

где R – суммарное сопротивление, включающее в себя внутреннее сопротивлениеrисточника тока и сопротивление внешней цепи.

Выражение (2.21) или (2.22) есть закон Ома в интегральной (обобщенной) формедля цепи постоянного тока.

Действительно, если на данном участке цепи источник тока отсутствует(), то из (2.22) приходим к закону Ома для однородного участка цепи:

Если электрическая цепь замкнута(точки 1 и 2 совпадают), то. Тогда из (2.22) получаемзакон Ома для замкнутой цепи:

Наконец, если цепь разомкнута, тои из (2.22) получаем, что, следовательно, для экспериментального определения ЭДС источника тока необходимо измерить разность потенциалов на его зажимах при разомкнутой нагрузке (режим холостого ходацепи).

Расчет разветвленных цепей постоянного тока

Закон Ома в интегральной форме позволяет рассчитывать практически любую электрическую цепь. Однако непосредственный расчет разветвленных цепей, содержащих замкнутые контуры, достаточно сложен. Эта задача упрощается при использовании правил Кирхгофа (немецкий физик, XIXв.).

Любая точка разветвленной электрической цепи, в которой сходится не менее трех проводников тока, называется узлом. При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла – отрицательным (рис. 2.9).

Первое правило Кирхгофасформулировано для узла электрической цепи:алгебраическая сумма сил токов в узле электрической цепи равна нулю, то есть

где n – число проводников, сходящихся в узле.

Таким образом, при указанных на рис. 2.9 направлениях токов в проводниках первое правило Кирхгофа запишется в виде

Первое правило Кирхгофа является следствием закона сохранения электрического заряда.

Второе правило Кирхгофавытекает из закона Ома в интегральной форме для разветвленных цепей. Выделим в сложной электрической цепи замкнутый контур, состоящий из трех участков (рис. 2.10). Условимся обходить контур по часовой стрелке. Все токи, совпадающие по направлению с выбранным направлением обхода контура, считаются положительными. ЭДС источников считаются положительными, если они создают ток, направленный в сторону обхода контура. Применяя к отдельным участкам контура закон Ома, запишем:

Складывая почленно эти уравнения, получим

Таким образом, второе правило Кирхгофа гласит: в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС источников равна алгебраической сумме падений напряжений на отдельных участка этого контура, то есть

где n– количество источников тока в контуре;m– число участков в контуре.

При расчете сложных цепей постоянного тока с применением правил Кирхгофа следует придерживаться следующих рекомендаций:

1. Произвольно выбирают направления токов в ветвях цепи. Действительные направления токов в схеме определяются после завершения расчетов: если искомый ток получился положительным, то его направление было выбрано правильно, если отрицательным – его истинное направление противоположно выбранному.

2. Выбирают направления обхода замкнутых контуров цепи (по часовой или против часовой стрелке). Произведение положительно, если ток на данном участке совпадает по направлению с направлением обхода; ЭДС, действующие по направлению обхода, считаются положительными, против направления обхода – отрицательными.

3. Составляют столько уравнений, чтобы их число было равно числу неизвестных токов, то есть числу ветвей в схеме. По первому правилу Кирхгофа составляют n-1 уравнений, гдеn– число узлов в схеме. Остальные уравнения составляют по второму правилу Кирхгофа.

4. Для проверки расчетов составляют баланс мощностив цепи:алгебраическая сумма мощностей источников тока равна сумме мощностей, рассеиваемых в ветвях схемы, то есть

где n – число источников тока в цепи;m– количество ветвей в схеме.