Часть 2.Аппроксимация экспериментальных данных

Экспериментальные данные могут быть заданы в виде таблицы n пар чисел X_i; Y_i. Аппроксимировать их, значит построить функцию, которая пройдет как можно ближе к заданным точкам. Существует много численных методов решения этой задачи. Некоторые из них запрограммированы в пакете MathCad. На рис. 25 приведен пример линейной аппроксимации 7-ми пар чисел, занесенных в массивы X_i, Y_i.

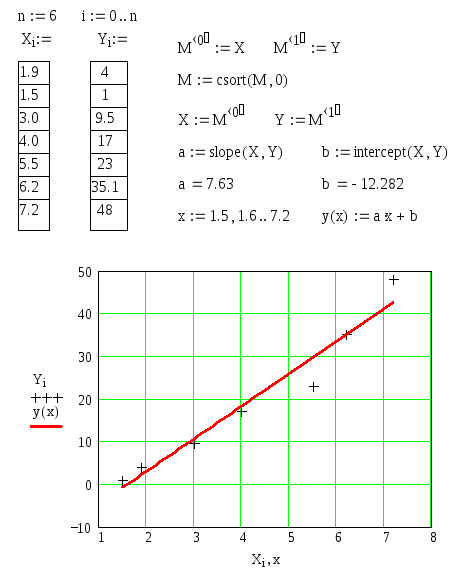
Рис. 25

Линейная аппроксимация предполагает построение прямой y(x) = ax + b, проходящей через заданные точки. Коэффициент а можно получить с помощью функции slope(X,Y), свободный член получаем с помощью функции intercept(X,Y). Следует иметь в виду, что эти функции работают с упорядоченным по возрастанию массивом X. Для упорядочения обоих массивов воспользуемся следующим приемом. Числа Х запишем в нулевой столбец двумерного массива М, числа Y запишем в первый столбец этого массива. Затем следует воспользоваться функцией csort(M,0), осуществляющей сортировку массива М по возрастанию нулевого столбца. После этого отсортированные пары чисел снова переписываются в массивы X и Y. Теперь можно вычислить коэффициенты a и b. Для приведенного примера они получились равными 7,63 и –12,282. Таким образом, искомая аппроксимирующая прямая имеет вид у(х) = 7,63х – 12,282. В принципе можно считать, что поставленная задача решена. Однако можно еще построить график, подсчитать абсолютную погрешность аппроксимации по формуле _i = Y_i – y(X_i), относительную погрешность по формуле .

Задание 1. Повторите линейную аппроксимацию вышеприведенного примера. Постройте графики, подсчитайте абсолютную и относительную погрешности аппроксимации.

MathCad имеет возможность осуществить нелинейную аппроксимацию полиномом k-й степени. Степень аппроксимирующего полинома выбирается с помощью столбца, содержащего члены полинома без коэффициентов, начиная с низшей степени (т.е. с нулевой). Аппроксимация полиномом выполняется с помощью функции linfit(X, Y, f ), где f – имя столбца, содержащего члены полинома. Результатом выполнения этой функции являются коэффициенты аппроксимирующего полинома.

На рис. 26 приведен пример аппроксимации данных из предыдущего примера полиномом 3-й степени.

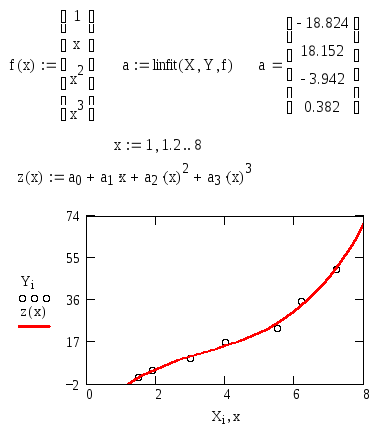
Рис. 26

Задание 2. Постройте аппроксимирующие полиномы 2-й и 3-й степени. Сравните погрешности линейной аппроксимации с погрешностями аппроксимации 2- и 3-й степеней. Постройте на одном поле графики линейной аппроксимации и аппроксимации 2-й и 3-й степеней.

Оглавление

ВВЕДЕНИЕ 2

Работа № 1 4

Часть 1. Значения переменных и функций, график функции одной переменной 4

Часть 2. Операции с матрицами, массивами 8

Работа № 2 11

Часть 1. Графика 11

Часть 2. Решение алгебраических уравнений 14

Работа № 3 17

Часть 1. Решение систем алгебраических уравнений. Численное интегрирование 17

Часть 2. Дифференцирование функций. Решение дифференциальных уравнений 20

Работа №4 23

Часть 1. Системы дифференциальных уравнений. Дифференциальные уравнения высших порядков 23

Часть 2. Аппроксимация экспериментальных данных 26

Оглавление 28

28