
УчебПособие (Теория надежности)2011
.pdf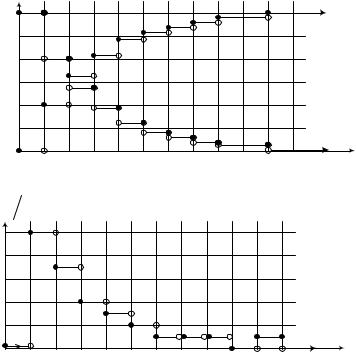
в) Построение графиков вероятности безотказной работы |
||||||||||||
|
|
|
|
|
|
|
|
^ |
|
|
|
|
P БР (t) , |
вероятности |
отказа |
Q(t) , |
плотности |
распределения |
|||||||
^ |
|
|
|
|
|
|
|
|
^ |
|
|
|
отказов f (t) |
и интенсивности отказов h(t) . |
|
|
|
||||||||
Графики данных функций представлены на рис. 4.4. |
|
|||||||||||
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
PБР |
(t), |
Q(t) |
|
|
|
|
|
|
|
^ |
|
30/30 |
|
|
|
|
|
|
|
|
|
|
Q(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20/30 |
|
|
|
|
|
|
|
|
|
|
|
|
10/30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P БР (t) |
|
0 |
20 |
40 |
60 |
|
80 |
100 120 140 160 180 200 220 |
t |
|||||
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (t) 600 |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
100 120 140 160 180 200 220 |
|
||||||
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
^ |
^ |
^ |
^ |
Рис. 4.4 (начало). Графики статистических оценок P БР (t) , |
Q(t ) |
f (t ) |
и h(t) : а – |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
^ |
|
графики статистических оценок вероятности безотказной работы P БР (t) и |
||||||||||||
|
|
^ |
|
|
|
|
|
|
|
|
|
|
вероятности отказа Q(t ) ; б – графики статистической оценки плотности распределения |
||||||||||||
|
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
отказов f (t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
61 |
|
|
|
|
^
h(t) / 600
30
25
20
15
10
5
t
0 |
20 |
40 |
60 |
80 |
100 120 140 160 180 200 220 |
|
||
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|
^ |
^ |
^ |
^ |
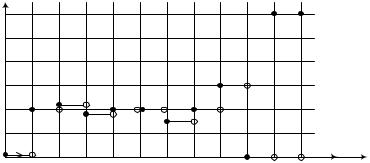
Рис. 4.4 (окончание). Графики статистических оценок P БР (t) , Q(t ) |
f (t ) |
и h(t) : |
||||||
|
|
|
|
|
|
|
^ |
|
в – графики статистической оценки интенсивности отказов h(t)
2) Расчёт числовых характеристик.
а) Оценка средней наработки до отказа.
|
k ~ |
|
^ |
~ |
|
|
|
t . |
|
|
|
|
||
t 0 |
ti |
Pi |
, где t i |
ti |
|
|
|
|
|
|||||
|
i 1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
~ |
|
|
|
t |
|
20 |
|
|
|
~ |
130 ; |
|||
t 1 |
tmin |
|
20 |
30 |
; |
t |
6 |
|||||||
2 |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
~ |
t2 |
t |
40 10 50 ; |
|
|
~ |
|
|
||||||
t 2 |
|
2 |
|
|
150 ; |
|||||||||
|
|
|
t 7 |
|||||||||||
~ |
|
|
|
|
|
|
|
|
||||||
70 ; |
|
|
|
|
|
|
|
|
~ |
|
|
|||
t 3 |
|
|
|
|
|
|
|
|
170 ; |
|||||
|
|
|
|
|
|
|
|
t |
8 |
|||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
||
90 ; |
|
|
|
|
|
|
|
|
~ |
|
|
|||
t 4 |
|
|
|
|
|
|
|
|
190 ; |
|||||
|
|
|
|
|
|
|
|
t |
9 |
|||||
~ |
|
|
|
|
|
|
|
|
|
|
|
|
||
110 ; |
|
|
|
|
|
|
|
~ |
|
|
||||
t 5 |
|
|
|
|
|
|
|
|
210 . |
|||||
|
|
|
|
|
|
|
t |
10 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
62
|
30 |
10 |
50 |
|
7 |
|
|
70 |
|
4 |
|
90 |
3 |
|
110 |
2 |
130 |
1 |
|
150 |
1 |
|
|||||||||||||||||||||
t 0 |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
30 |
30 |
|
30 |
30 |
|
|
30 |
|
30 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|||||||||||||||||
170 |
1 |
190 0 210 |
1 |
|
|
|
2080 |
|
69,3 (ч). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
69,3 (ч). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) Оценка дисперсии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
k |
~ |
|
|
|
|
|
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
D |
(t |
t |
0 |
|
)2 P |
i |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
10 |
|
|
|
|
|
|
|
|
|
2 |
|
|
7 |
|
|
|
|
2 |
|
4 |
|
|
|
|
||||||||
D |
(30 |
69, 3) |
|
|
(50 |
69, 3) |
|
|
|
(70 69, 3) |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
30 |
|
|
|
|
30 |
|
30 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(90 69, 3)2 |
|
3 |
|
(110 69, 3)2 |
|
2 |
|
(130 69, 3)2 |
1 |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
30 |
|
|
|
|
|
|||||||||
(150 69, 3)2 |
|
1 |
|
|
|
(170 69, 3)2 |
|
1 |
|
(190 69, 3)2 |
0 |
|
|
|
|||||||||||||||||||||||||||||
30 |
|
30 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(210 69,3)2 |
|
1 |
2093 (ч2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
D 2093 (ч2).
в) Оценка среднего квадратического отклонения.
 D
D 
 2093 46 (ч).
2093 46 (ч).
3) Выбор закона распределения наработки до отказа.
Параметры безотказности, рассчитанные на отрезках t, расположенных по краям интервала t, в которых число отказов мало (равно 1) имеют низкую достоверность, поэтому при выборе закона распределения они во внимание не принимаются. В нашем случае это отрезки t6 = (120;140); t7 = (140;160); t8 = (160;180); t9 = (180;200);
t10 = (200;220).
Анализ графиков на интервале от 20 ч до 120 ч показывает, что формы эмпирических функций безотказности наиболее близки к экспоненциальному закону распределения, для которого f (t) e t , h(t) const .
63
|
|
|
|
1 |
|
|
|
1 |
|
|||
Так как t 0 |
, то |
t 0 |
|
. Следовательно, |
||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
0, 0144 (1/ч). |
|||||||
|
69,3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
|
||
Окончательно теоретическое распределение наработки до отказа имеет вид
0 при 0 t 20;
f (t) 0, 0144 e 0,0144 t при 20 t 220;
0 при t 220.
Вопросы для самоподготовки
1.Какие способы сбора статистической информации об отказах и восстановлениях объектов электроэнергетики Вы знаете? Перечислите их достоинства и недостатки.
2.По какой формуле определяется частота появления отказов для объектов первой категории? С кривой какого показателя безотказности совпадает по форме ее график?
3.По каким формулам, используя данные статистического ряда, рассчитываются статистические оценки числовых характеристик?
4.Перечислите основные этапы алгоритма обработки результатов экспериментов.
Задачи для самоподготовки
Задача №1. При наблюдении за работой 50 однотипных невосстанавливаемых объектов был получен следующий статистический ряд наработок до отказа:
Tα = {5; 5,05; 5,08; 5,09; 5,1; 5,1; 5,12; 5,15; 5,21; 5,21; 5,27; 5,29; 5,3; 5,31; 5,34; 5,35; 5,42; 5,43; 5,46; 5,47; 5,55; 5,59; 5,67; 5,72; 5,75; 5,78; 5,82; 5,84; 5,92; 5,94; 5,96; 5,99; 6,07; 6,14; 6,18; 6,25; 6,29; 6,35; 6,42; 6,56; 6,69; 6,77; 6,93; 7,1; 7,25; 7,42; 7,65; 7,95; 8,29; 9} (лет).
Разбив интервал наработки на k = 8 участков, определить:
1) зависимость от времени показателей безотказности: вероятности
|
|
|
|
^ |
безотказной |
работы |
P БР (t) , вероятности |
отказа |
Q(t) , плотности |
|
|
^ |
|
^ |
распределения |
отказов |
f (t) и интенсивности |
отказов |
h(t) ; построить их |
графики; |
|
|
|
|
|
|
64 |
|
|

2) числовые характеристики: среднюю наработку до отказа t0 ,
дисперсию наработки до отказа D и ее среднее квадратическое отклонение
;
3) закон распределения наработки до отказа.
Задача №2. При наблюдении за работой 30 однотипных невосстанавливаемых объектов был получен следующий статистический ряд наработок до отказа:
Tα = {1; 1,1; 1,2; 1,3; 1,4; 1,5; 1,5; 1,6; 1,7; 1,9; 2,1; 2,2; 2,2; 2,4; 2,5; 2,5; 2,5; 2,7; 2,9; 3; 3,1; 3,2; 3,2; 3,3; 3,5; 3,7; 3,8; 3,9; 3,9; 4} (ч).
Разбив интервал наработки на k = 6 участков, определить:
1) зависимость от времени показателей безотказности: вероятности
|
|
|
|
^ |
безотказной |
работы |
P БР (t) , вероятности |
отказа |
Q(t) , плотности |
|
|
^ |
|
^ |
распределения |
отказов |
f (t) и интенсивности |
отказов |
h(t) ; построить их |
графики;
2) числовые характеристики: среднюю наработку до отказа t0 ,
дисперсию наработки до отказа D и ее среднее квадратическое отклонение
;
3) закон распределения наработки до отказа.
65
Глава 5. Методы и задачи расчета надежности электроэнергетических объектов
5.1 Метод пространства состояний
5.1.1.Постановка задачи
Имеются объекты, являющиеся системой, которая состоит из некоторого количества элементов. Каждый элемент может находиться в нескольких состояниях. Количество состояний каждого элемента конечно. Состояние системы определяется состоянием каждого элемента системы. Если изменяется состояние одного из элементов, то система переходит в новое состояние. Все возможные состояния системы образуют пространство состояний. Необходимо определить вероятности нахождения системы в том или ином состоянии с помощью метода пространства состояний.
5.1.2. Математическая модель надежности системы
При использовании метода пространства состояний в общем случае для системы S необходимо иметь математическую модель в виде множества состояний, в которых она может находиться.
Основные правила составления модели:
1. Математическую модель изображают в виде диаграммы пространства состояний или графа состояний (рис. 5.1).
|
qi j t |
1 q t |
Si |
i |
Sj |
n |
|
1 qi j t |
q j i t |
|
j i j 1
Рис. 5.1. Диаграмма (граф) пространства состояний
66

Элементами диаграммы пространства состояний являются
кружки (вершины графа S1, S2, …, Sn) и стрелки. Кружки –
возможные состояния системы S, а стрелки – возможные направления переходов из одного состояния Si в другое Sj. Стрелки являются событиями.
Над или под стрелками указываются вероятности переходов из одного состояния в другое.
Петлёй обозначаются задержки в том или ином состоянии. Диаграмма пространства состояний отображает конечное
(дискретное) число возможных состояний системы.
2. Для описания случайного процесса перехода из состояния в состояние применяются вероятности состояний (см. п. 1.2) P1(t), P2(t), …, Pn(t). Pi(t) = P(S(t) = Si) – вероятность нахождения системы в момент времени t в i-м состоянии.
Для любого времени t выполняется условие нормировки:
|
|
|
|
n |
|
|
|
|
|
|
Pi (t) 1 . |
|
(5.1) |
|
|
|
|
i 1 |
|
|
3. По диаграмме пространства состояний составляется система |
||||||
обыкновенных |
|
дифференциальных |
уравнений первого порядка |
|||
(система уравнений Чемпена – Колмогорова): |
|
|||||
|
dPi |
(t) |
|
n |
n |
|
|
|
qi j Pj (t) Pi |
(t) qi j . |
|
||
|
dt |
(5.2) |
||||
|
|
j 1 |
j 1 |
|||
|
|
|
|
|
||
|
|
|
|
j i |
j i |
|
Интенсивности переходов qj i и qi j должны быть постоянными величинами, т. е. независимыми от времени. Это возможно, когда все случайные величины, используемые в математической модели, распределены по экспоненциальному закону.
При составлении дифференциальных уравнений пользуются простейшим мнемоническим правилом:
- в левой части записываются производные по времени t от вероятности нахождения системы в каждом из возможных состояний
( dPi (t) ); dt
-число членов в правой части равно числу стрелок, соединяющих рассматриваемое состояние с другими состояниями;
-каждый член правой части равен произведению интенсивности перехода на вероятность того состояния, из которого выходит стрелка;
-знак произведения положителен, если стрелка входит в рассматриваемое состояние, и отрицателен, если стрелка выходит.
67
Проверкой правильности составления уравнений является равенство нулю суммы правых частей уравнений.
4 Чтобы решить систему дифференциальных уравнений для вероятностей состояний P1(t), P2(t), …, Pn(t), необходимо задать начальное значение вероятностей P1(0), P2(0), …, Pn(0) при t = 0, сумма
n
которых равна 1, Pi (0) 1 . i 1
Если в начальный момент t = 0 состояние системы известно, например система S находится в i-м состоянии и Pi(0) = 1, то вероятности нахождения системы в любом другом состоянии равны 0.
Во многих приложениях интерес представляют только асимптотические значения вероятностей, в которых время наблюдения за системой стремится к бесконечности: P(t→ ). При возрастании периода наблюдения изменение Pi(t) уменьшается и при t→ :
|
|
|
dPi |
(t ) |
0 . |
|
|
(5.3) |
|
|
|
|
dt |
|
|
||
|
|
|
|
|
|
|
|
|
Тогда уравнение Чемпена – Колмогорова представляется в виде |
||||||||
|
|
n |
|
|
n |
|
|
|
|
0 |
qi j Pj (t) Pi (t) |
qi j . |
|
(5.4) |
|||
|
j 1 |
|
|
j 1 |
|
|||
|
|
|
|
|
||||
|
j i |
|
|
j i |
|
|
||
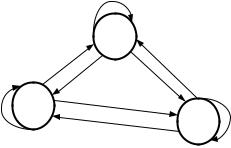
Пример составления системы уравнений Чемпена – |
||||||||
Колмогорова с тремя возможными состояниями системы. |
|
|||||||
В начале |
составляем диаграмму пространства |
состояний |
||||||
(рис. 5.2): |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 q2 t |
|
|
|
|
|
|
|
|
1 q2 1 t q2 3 t |
|
||
|
q1 2 t |
S2 |
|
|
|
|
||
|
|
|
q3 2 t |
|
|
|||
|
|
|
|
q2 3 t |
|
|
||
|
|
|
q2 1 t |
|
|
|
|
|
1 q1 t |
S1 |
q1 3 t |
S3 |
1 q3 t |
|
|||
|
|
|
q3 1 t |
1 q3 2 |
t q3 1 |
|||
1 q1 2 t q1 3 t |
|
|||||||
Рис. 5.2. Диаграмма пространства состояний для системы с тремя состояниями
68

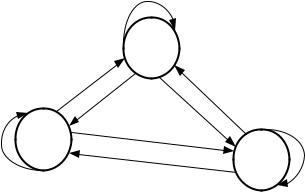
На основании диаграммы пространства состояний записываем систему уравнений Чемпена – Колмогорова:
dP (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
P (t) (q |
|
q |
) P (t) q |
|
P (t) q |
1, |
||||||
|
|
|
|
|
|
||||||||||||
dt |
1 |
1 3 |
|
1 2 |
2 |
2 1 |
3 |
3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dP2 |
(t) |
P (t) q |
P (t) (q |
|
q |
) P (t) q |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||
dt |
1 |
1 2 |
|
2 |
|
2 1 |
2 3 |
|
3 |
3 2, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dP3 |
(t) |
P (t) q |
P (t) q |
|
P (t) (q |
|
q |
|
). |
|||||||
|
|
|
|
|
|
||||||||||||
dt |
1 |
1 3 |
|
2 |
2 3 |
|
3 |
3 1 |
3 2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так как из любых двух уравнений системы можно вывести третье, то при трех неизвестных имеем два независимых уравнения. Следовательно, чтобы решить систему, нужно составить еще одно независимое уравнение. Им является условие нормировки:
P (t) P (t) P (t) 1 . |
||
1 |
2 |
3 |
5.1.3. Связь частоты возникновения и продолжительности состояния с вероятностью нахождения системы в i-м состоянии и интенсивностью переходов для стационарных процессов
Частота появления i-го состояния i определяется как ожидаемое число пребываний системы в состоянии Si в единицу времени при достаточно длительном наблюдении.
Чтобы связать частоту i, вероятность Pi и среднюю продолжительность данного состояния системы ti , рассмотрим процесс функционирования системы, как состоящий из двух чередующихся интервалов времени – пребывание в состоянии Si и пребывание вне этого состояния. Таким образом, система описывается процессом с двумя состояниями. Диаграмма пространства состояний для этого случая показана на рис 5.3.
Обозначим ti как среднюю продолжительность пребывания вне состояния Si.
Среднее время цикла в этом случае равно |
|
|||||
|
|
|
|
|
|
|
tцi |
ti ti . |
(5.5) |
||||
Тогда |
|
|
|
|
|
|
i |
|
1 |
. |
(5.6) |
||
|
||||||
|
|
|
tцi |
|
||
|
69 |
|
||||

Si |
Все прочие |
|
состояния |
||
|
Рис. 5.3. Процесс работы системы с двумя состояниями: «в состоянии i» и «вне состояния i»
Если умножить уравнение (5.6) на ti , то правая часть примет
вид |
ti |
, который соответствует |
геометрическому определению |
|||
tцi |
||||||
|
|
|
|
|
||
вероятности Pi. Тогда |
|
|
||||
|
|
ti P . |
(5.7) |
|||
|
|
i |
i |
|
||
|
Уравнение (5.7) дает связь между рассмотренными в этом |
|||||
разделе тремя параметрами. |
|
|
||||
|
Теперь свяжем частоту i, среднюю продолжительность |
|||||
|
|
|
||||
данного состояния системы ti |
и интенсивность переходов системы. |
|||||
Для этого введем понятие частоты перехода из состояния i в состояние j. Эта частота ( i j) определяется как ожидаемое число переходов из состояния i непосредственно в состояние j в единицу времени. Следовательно,
|
q |
P |
i j |
i j |
i |
(подробный вывод формулы приведен в [3]). Из определения i и i j следует, что
n |
|
i |
i j . |
j i |
|
j 1 |
|
Подставляя в это выражение уравнение (5.8), получаем
(5.8)
(5.9)
n |
|
|
i Pi qi j . |
(5.10) |
|
j i |
||
|
||
j 1 |
|
Наконец, объединяя (5.7) и (5.10), получаем выражение для t i :
70
