УчебПособие (Теория надежности)2011

Из априорных способов наиболее часто используется подход,

основанный на понятии классического определения вероятности

(понятии равновозможных исходов).

Классическая вероятность наступления события Е – это отношение числа благоприятствующих событию Е исходов (m) к общему числу всех несовместных элементарных исходов (n), образующих полную группу:

n

Из апостериорных подходов можно выделить подход,

основанный на понятии статистического определения вероятности (метод относительной частоты).

Относительной частотой события называется отношение числа испытаний, в котором событие появилось (k), к общему числу фактически произведённых испытаний (r):

В качестве статистической вероятности события принимают относительную частоту или число, близкое к ней. Это приближение улучшается по мере роста r, и точное значение определяется формулой

Кроме рассмотренных выше методов, можно выделить подход,

основанный на понятии геометрического определения вероятности. Геометрическая вероятность – это вероятность попадания

точки в область (отрезок, часть плоскости и т.д.).

Пусть отрезок l составляет часть длины отрезка L. Точка А на этом отрезке поставлена наудачу (рис. 1.8).

l

A

L

Рис.1.8. Пояснение к понятию «геометрическая вероятность»

Предположения, принятые при этом:

- поставленная точка может оказаться в любой точке отрезка L;

11

- вероятность попадания точки А на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L.

В этом случае вероятность попадания точки А на отрезок l (событие Е) определяется равенством:

L

1.3.2. Условная вероятность

Часто случается, что вероятность какого-то события А зависит от того, произошло или не произошло событие В. В этом случае вероятность возникновения события А является условной и для ее обозначения используют следующую форму записи: P[A/B].

Общая формула условной вероятности:

В общем случае, если вероятность какого-то события А условна относительно нескольких событий В1, В2, …, Вn, которые являются несовместными и в сумме составляют достоверное событие, то полная вероятность события А определяется по формуле полной вероятности:

n

P[A] P[A/Bi ] P[Bi ] . (1.10) i 1

1.3.3. Формулы вычисления вероятностей

1) Если событие A является дополнением А, то

2) Сумма вероятностей событий А1, А2, …, Аn, образующих пространство элементарных событий (полную группу), равна:

В общем случае:

12

n

P[A1 A2 A3 ... An ] P[Ai ] . (1.18) i 1

Случай, когда события независимы:

n

P[A1 A2 A3 ... An ] P[Ai ] ; (1.19) i 1

5) Вероятность появления хотя бы одного из событий А1, А2, …, Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположенных событий A1, A2,

…, An:

n

P[A] 1 P[ Ai ]. (1.21) i 1

1.4. Случайные величины и их распределение

1.4.1. Случайная величина Случайная величина – это величина, которая в результате

испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не

13

могут быть учтены. Случайные величины могут быть непрерывными и дискретными.

Пример дискретной случайной величины – выпадение количества очков на кубике; сторона монеты при ее подбрасывании.

Пример непрерывной случайной величины – величина сопротивления резистора, наугад взятого из партии; средняя температура воздуха за сутки.

1.4.2. Дискретные случайные величины А. Закон распределения дискретной случайной величины – это

перечень возможных значений случайной величины и соответствующих им вероятностей.

Закон может быть представлен в трех видах:

1) в графическом, с помощью многоугольника распределения

(рис. 1.9):

P

P3

P2

P1

X

Рис. 1.9. Многоугольник распределения

2) аналитическом:

P[X xi ] (xi ) ;

3) в виде таблицы:

Б. Закон Пуассона. Распределение, или формула Пуассона, используется, когда требуется найти вероятность того, что при очень большом числе испытаний n, в каждом из которых вероятность события p очень мала, событие наступит ровно k раз.

Распределение Пуассона имеет вид

Здесь – среднее число испытаний, при котором появлялось рассматриваемое событие

В. Простейший (пуассоновский) поток событий. Поток событий – последовательность событий, которые наступают в случайные моменты времени.

Простейшим, или пуассоновским, потоком событий называется поток событий, который обладает следующими свойствами:

-стационарностью;

-отсутствием последствий;

-ординарностью.

Свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке времени t зависит только от числа k и длительности промежутка t и не зависит от начала его отсчёта.

Свойство отсутствия последствий характеризуется тем, что вероятность появления k событий на любом промежутке времени t не зависит от того, появились или не появились эти события в момент времени, предшествующий началу этого промежутка.

Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени почти невозможно.

Интенсивность потока событий – среднее число событий,

которое появляется за единицу времени.

Можно доказать, что если постоянная интенсивность потока известна, то вероятность появления k событий за время t определяется формулой

Эта формула отражает все свойства простейшего потока.

15

Г. Числовые характеристики дискретной случайной величины.

Они описывают случайную величину суммарно.

Математическое ожидание дискретной случайной величины –

сумма произведений всех её возможных значений на её вероятность:

Можно показать, что математическое ожидание дискретной случайной величины равно среднему арифметическому наблюдаемых значений случайной величины.

Дисперсия – математическое ожидание квадрата отклонений случайной величины от её математического ожидания:

Среднее квадратическое отклонение случайной величины:

1.4.3. Непрерывные случайные величины А. Интегральная функция распределения вероятности.

Поскольку непрерывная случайная величина принимает бесконечное число значений, то задать распределение её в таком виде, как для дискретной случайной величины, невозможно. Поэтому для задания распределения любой случайной величины вводят интегральную функцию распределения вероятности F(x), где х – действительное число.

Вероятность события, состоящего в том, что случайная величина Х примет значение Х < x, – это интегральная функция распределения вероятности

Пример формы кривой F(x) представлен на рис. 1.10.

Свойства интегральной функции распределения вероятности:

1) Ее значения принадлежат отрезку [0; 1]:

2) Она всегда возрастает (неубывает), то есть если x1 < x2, то

F

1

Рис.1.10. Пример формы кривой интегральной функции распределения вероятности F(x)

Из второго свойства вытекает следующее:

- вероятность того, что случайная величина Х попадет на

Для дискретной случайной величины можно построить интегральную функцию распределения вероятностей, только она будет иметь ступенчатый вид.

Б. Плотность распределения вероятности непрерывной случайной величины. Непрерывную случайную величину можно также задать, используя другую функцию, которая называется плотностью распределения вероятности.

Зная плотность распределения вероятности, можно вычислить вероятность того, что случайная величина примет значение, принадлежащее интервалу (a; b):

f [x]dx 1. (1.38)

В. Числовые характеристики непрерывной случайной величины.

Определение числовых характеристик дискретных случайных величин можно распространить и на величины непрерывные.

Математическое ожидание

M [X ] x f [x]dx . (1.39)

Г. Законы распределения вероятностей непрерывной случайной величины. Плотность распределения вероятности непрерывной

случайной величины называется также законом распределения вероятностей. На практике эти законы используются на выбор, когда результаты эксперимента согласуются с тем или иным законом распределения вероятности.

Чтобы облегчить процесс подбора подходящего закона распределения вероятности, введём ещё одну функцию, которую называют интенсивностью потока событий:

18

Равномерный закон распределения вероятности описывается

Интенсивность потока событий в аналитическом виде:

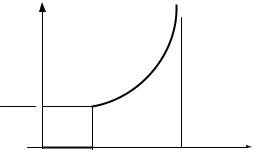
Интенсивность потока событий в графическом виде (рис. 1.12):

h

с 1 b a

Рис. 1.12. Форма кривой интенсивности потока событий h(x) при равномерном законе распределения непрерывной случайной величины

В энергетике равномерному закону почти ничто не подчиняется.

2. Экспоненциальный (показательный) закон распределения вероятности непрерывной случайной величины.

Аналитический вид:

20