- •Курс Твердотельной электроники
- •1. Физические основы твердотельной электроники
- •1.1. Диффузионный и дрейфовый ток в полупроводниках
- •1.2. Зависимость подвижности от концентрации примесей,
- •1.3. Фундаментальная система уравнений
- •1.4. Обеднение, обогащение и инверсия
- •1.5. Потенциальный барьер
- •1.6. Область пространственного заряда p-n перехода
- •1.7. Зависимость концентраций неосновных неравновесных носителей зарядов на границах от напряжения на переходе
- •1.8. Рекомбинация неравновесных носителей заряда
- •1.9. Условия на контактах и поверхностная рекомбинация
- •1.10. Распределение неосновных носителей заряда вблизи p-n-перехода
- •2. Элементы и процессы твердотельной электроники
- •2.1. Распределение носителей и коэффициент передачи тока в транзисторной структуре
- •2.2. Физическая структура биполярного транзистора
- •2.3. Биполярные транзисторы интегральных схем
- •2.4. Кремниевые транзисторы свч диапазона
- •2.5. Энергетическая диаграмма контакта металл-полупроводник
- •2.6. Токи в контакте металл-полупроводник
- •2.7. Гетеропереходы
- •2.8. Туннелирование в p-n-переходе
- •2.9. Лавинное умножение
- •2.10. Структура металл-диэлектрик-полупроводник
- •2.11. Пороговое напряжение мдп транзистора
- •2.12. Вольт-амперная характеристика мдп транзистора
- •2.13. Конструктивные разновидности мдп транзисторов
- •2.13.1. Мощные моп транзисторы
- •2.13.2. Элементы сбис
- •2.14. Элементы зу на мдп транзисторах
- •2.14.1. Мноп транзистор
- •2.14.2. Транзисторы с плавающим затвором
- •2.15. Приборы с зарядовой связью
- •2.15.1. Передача заряда между затворами
- •2.15.2. Накопление заряда в моп структурах
- •2.15.3. Связь между зарядом и поверхностным потенциалом
- •2.15.4. Перенос заряда под затвором
- •3. Основные технологические процессы микроэлектроники
- •3.1. Диффузия
- •3.2. Окисление
- •3.3. Ионное легирование
- •3.3.1. Распределение Гаусса
- •3.3.2. Другие распределения
- •3.3.3. Боковое уширение распределения ионов
- •3.4. Эпитаксия
- •4. Курсовое проектирование
- •4.2. Резкий p-n-переход
- •4.3. Диффузионные переходы
- •4.4. Токи диффузионных переходов
- •4.5. Биполярный транзистор интегральных схем
- •4.6. Малосигнальные параметры биполярных транзисторов
- •4.7. Полевой транзистор с управляющим p-n-переходом
- •4.8. Полевой транзистор с изолированным затвором
Курс Твердотельной электроники
1. Физические основы твердотельной электроники
1.1. Диффузионный и дрейфовый ток в полупроводниках
Дрейфовые
токи совпадают по направлению с вектором
напряженности электрического поля
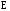 и пропорциональны его модулю. Коэффициент
пропорциональности между напряженностью
и плотностью тока называется
электропроводностью
и пропорциональны его модулю. Коэффициент
пропорциональности между напряженностью
и плотностью тока называется
электропроводностью и представляет собой произведение
заряда электрона
и представляет собой произведение
заряда электрона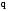 ,
концентрации электронов
,
концентрации электронов или дырок
или дырок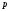 и соответствующих подвижностей
и соответствующих подвижностей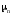 ,
,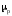 ,
т. е. скорости в единичном поле
,
т. е. скорости в единичном поле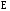 с напряженностью 1 В/см. Отдельно для
электронов и дырок:
с напряженностью 1 В/см. Отдельно для
электронов и дырок:
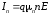
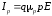
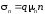
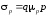
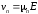
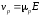
Распределения
концентраций в пространстве порождают
диффузионные компоненты потоков и
токов, пропорциональные градиентам,
перепадам концентраций. Ограничимся
одномерными распределениями концентраций
 ,
,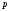 и потенциала
и потенциала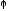 ,
,
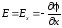 Знак
“минус” в этом выражении возникает
из-за того, что поле направлено от более
высокого потенциала к низкому. Градиенты
концентраций в одномерном случае будут
иметь по одной компоненте
Знак
“минус” в этом выражении возникает
из-за того, что поле направлено от более
высокого потенциала к низкому. Градиенты
концентраций в одномерном случае будут
иметь по одной компоненте
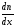 и
и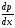 .
.
Диффузионные компоненты токов могут быть выражены как
Рис.
1.
Распределение концентраций и направления
потоков и токов при диффузии электронов
и дырок.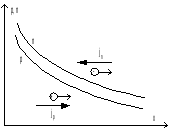
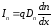 ,
, 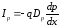 .
Минус в формуле дырочного диффузионного
тока связан с тем, что для дырок направления
тока и потока совпадают, а носители
всегда диффундируют в сторону убывания
концентраций. На рис. 1 показаны направления
диффузионных потоков и токов для
электронов и дырок.
.
Минус в формуле дырочного диффузионного
тока связан с тем, что для дырок направления
тока и потока совпадают, а носители
всегда диффундируют в сторону убывания
концентраций. На рис. 1 показаны направления
диффузионных потоков и токов для
электронов и дырок.
В условиях электронейтральности концентрации избыточных электронов и дырок примерно одинаковы. Стрелки при кружочках показывают направления потоков. Потоки направлены в сторону убывания концентраций, т. е. против градиентов. Для электронов направления потока и тока противоположны.
Подвижности и коэффициенты диффузии связаны между собой соотношениями Эйнштейна
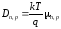 ,
,
где
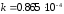 эВ/К
– постоянная Больцмана. При
эВ/К
– постоянная Больцмана. При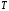 =290 К тепловой потенциал
=290 К тепловой потенциал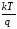 = 0.025 B.
= 0.025 B.
Величины
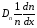 и
и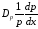 будут иметь смысл скоростей диффузии
аналогично скоростям дрейфа, а
будут иметь смысл скоростей диффузии
аналогично скоростям дрейфа, а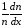 и
и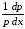 – некоторых обратных расстояний, на
которых происходят изменения концентраций.
Эти величины будут определяться
граничными условиями конкретных
структур.
– некоторых обратных расстояний, на
которых происходят изменения концентраций.
Эти величины будут определяться
граничными условиями конкретных
структур.
1.2. Зависимость подвижности от концентрации примесей,
температуры и электрического поля
Сложные кинетические эффекты, связанные с процессами релаксации импульса и энергии, могут быть качественно пояснены на основе простых моделей уравнений движения
 , (1.1)
, (1.1)
где 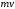 – импульс носителя заряда;
– импульс носителя заряда;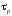 – время релаксации импульса,
– время релаксации импульса,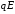 – электрическая составляющая силы
Лоренца.
– электрическая составляющая силы
Лоренца.
Производная
в левой части и первый член в правой
повторяют элементарный закон Ньютона
для материальной частицы с массой
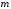 :
: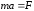 ,
где
,
где – ускорение. Второй член в правой части
отражает явление торможения из-за
столкновений (рассеяний) импульса,
происходящих с частотой
– ускорение. Второй член в правой части
отражает явление торможения из-за
столкновений (рассеяний) импульса,
происходящих с частотой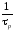 .
Стационарный дрейфовый импульс, который
устанавливается в постоянном поле
.
Стационарный дрейфовый импульс, который
устанавливается в постоянном поле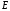 в условиях
в условиях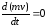 при
при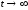 ,
,
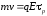 После
выключения поля
После
выключения поля

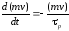 и
и
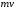 убывает из-за рассеяния по закону
убывает из-за рассеяния по закону
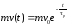 т. е. экспоненциально с постоянной
времени
т. е. экспоненциально с постоянной
времени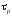 .
.
Стационарная дрейфовая скорость оказывается пропорциональна полю
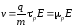 ,
так что
,
так что
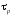 и подвижность
и подвижность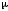 в слабом поле связаны между собой только
отношением заряда к эффективной массе
носителя.
в слабом поле связаны между собой только
отношением заряда к эффективной массе
носителя.
Время релаксации импульса зависит от температуры и концентрации рассеивающих центров из-за сложения частот столкновений
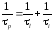 ,
где
,
где  – частота столкновений с колебаниями
решетки;
– частота столкновений с колебаниями
решетки;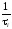 –
частота столкновений с ионами примеси.
–
частота столкновений с ионами примеси.
Термин "частота столкновений" не вполне точно отражает сложные процессы обмена импульсами между подвижными носителями и колебаниями решетки и изменения импульса в полях ионов, но вполне подходит для качественного объснения физики совместного действия примеси и температуры на подвижность. Существенно, например, что
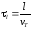 ,
где
,
где 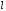 – длина свободного пробега на тепловых
колебаниях решетки, эта величина зависит
только от свойств материала и температуры
решетки, а
– длина свободного пробега на тепловых
колебаниях решетки, эта величина зависит
только от свойств материала и температуры
решетки, а – результирующая скорость, которая
складывается из тепловой скорости
беспорядочного движения и дрейфовой
скорости носителя в электрическом поле.
Результирующая скорость
– результирующая скорость, которая
складывается из тепловой скорости
беспорядочного движения и дрейфовой
скорости носителя в электрическом поле.
Результирующая скорость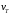 определяется уравнением переноса для
энергии
определяется уравнением переноса для
энергии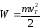 ,
которое может быть записано аналогично
(1.1):
,
которое может быть записано аналогично
(1.1):
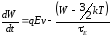
Это
уравнение также имеет своим аналогом
элементарное соотношение формулы для
работы
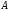 через силу
через силу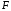 и расстояние
и расстояние ,
, ,
тогда
,
тогда
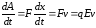
В
стационарных условиях и в отсутствии
поля
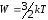 ,
в стационарных условиях энергия
увеличивается во внешнем поле
,
в стационарных условиях энергия
увеличивается во внешнем поле
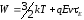
В
слабом поле
 и энергия растет пропорционально
квадрату поля. Опыт показывает, однако,
что в сильных полях скорость насыщается
и стремится к величине
и энергия растет пропорционально
квадрату поля. Опыт показывает, однако,
что в сильных полях скорость насыщается
и стремится к величине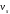 ,
такой, чтобы
,
такой, чтобы
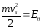
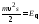 ,
,
где
 – энергия оптического фонона. Ограничение
дрейфовой скорости энергией оптических
фононов и определяет поведение носителей
в сильных полях. Такого рода соображения
делают понятным смысл аппроксимаций
зависимостей подвижностей и дрейфовых
скоростей от электрического поля. На
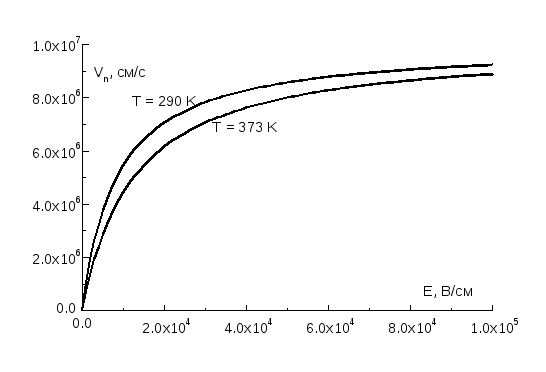
рис. 2 представлены зависимости дрейфовых
скоростей электронов в кремнии от
электрического поля при различных
температурах.
– энергия оптического фонона. Ограничение
дрейфовой скорости энергией оптических
фононов и определяет поведение носителей
в сильных полях. Такого рода соображения
делают понятным смысл аппроксимаций
зависимостей подвижностей и дрейфовых
скоростей от электрического поля. На
рис. 2 представлены зависимости дрейфовых
скоростей электронов в кремнии от
электрического поля при различных
температурах.
Рис.
2. Зависимости
дрейфовой скорости электронов от поля
при комнатной температуре Т = 290 К и при
температуре Т = 100 оС
(373 К). Концентрация
доноров 1015
см-3.
С ростом температуры уменьшается
решеточная подвижность и также несколько
уменьшается максимальная дрейфовая
скорость.