Криволинейные и поверхностные интегралы. Элементы теории поля.

1.

Демидович42 (21, 23, 26, 31,32,38, 50, 52,

59^*,64,71,72,74,83,84).

Вычислить криволинейные интегралы 1-го рода:

4221.,С–контур треугольника с вершинамиО(0,0), А(1,0), В(0,1).

4223.

4226..

4231.Найти длину дуги кривойx = 3t,y = 3t², z = 2t³ от О(0, 0, 0) до A(3,3,2).

4232.Найти длину дуги

4238.Вычислить .

Вычислить криволинейные интегралы 2-го рода:

4250.,в направлении возрастания величины х.

4252.,эллипс пробегается против часовой стрелки.

4259^*.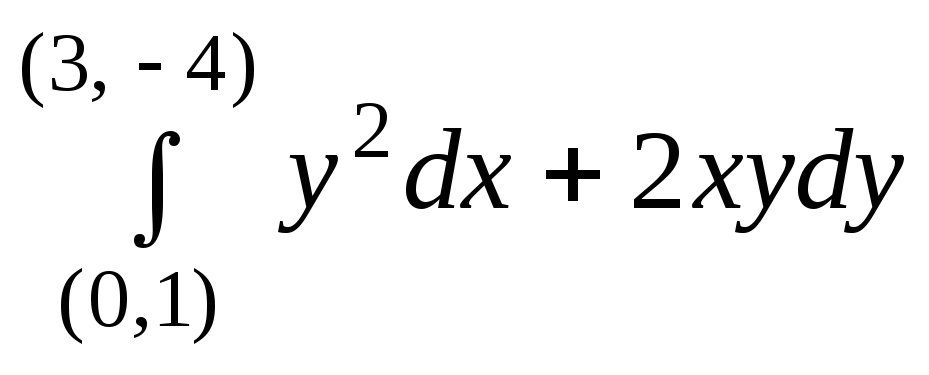

4264.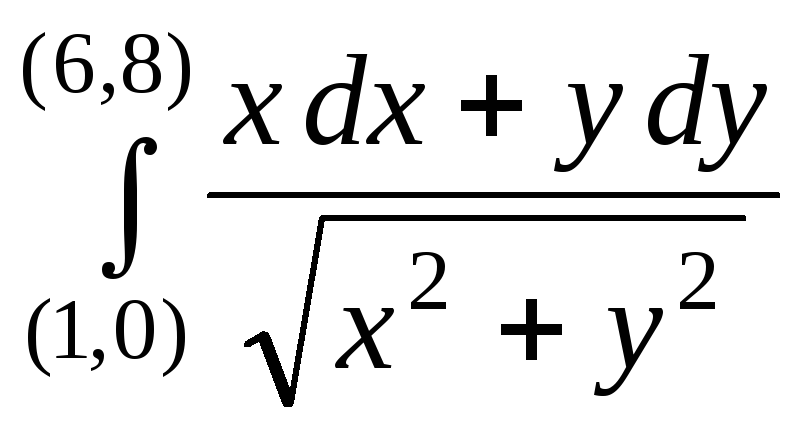вдоль путей, не проходящих через начало координат.

4271. Найти z(х,у),если .

24

Найти первообразную:

4272^*

4274^*

4283.Вычислить ,

гдеC–контур, ограничивающий часть сферы ,,пробегаемый так, что внешняя сторона поверхности остается слева

4284^*Вычислить:

.

.

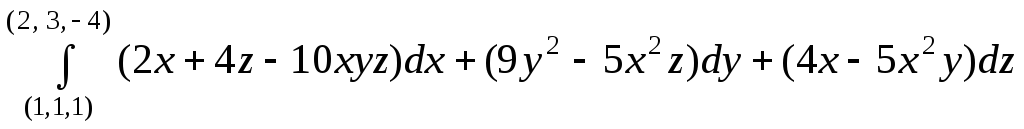2.

Демидович43(43,44, 45,52,62, 64, 68,70,73,77, 87,88).

Вычислить поверхностные интегралы :

4343..

4344..

4345..

4352.Найти массу параболической оболочки

(0< z <1) с плотностью.

4362..S – внешняя сторонасферы

x² + y² + z² = a².

4364.S–внешняя сторона поверхности:.

25

Применить формулу Стокса:

4368.AmB –отрезок винтовой линииот А(а,0,0) до В(а,0,h).

4370.:

x = asin²t, y = 2asintcost, z = acos²t, пробегаемый в направлении возрастания параметра t: .

4373.гдеС–сечение кубах[0,a],y[0,a],z[0,a]плоскостьюх+у+z = 3a/2,пробегаемый против часовой стрелки, если смотреть с положительной стороны осиОх.

Применяя формулу Остроградского, преобразовать:

4377..

4387.

.

4388.Вычислить,S–внешняя сторонасферыx² + y² + z² = a².

3.

Демидович44 ( 02,22.1,31, 36, 36.1,38, 39, 41, 42,44, 45, 45.1).

4402. В каких точках пространства Oxyz градиент поля U = x³ + y³ + z³ –3xyz: a) осиOz; б)  оси Oz; в) = 0.

4422.1.Найти дивергенцию поляв точкеМ(3,4,5).

26

Чему приближенно равен поток векторачерез бесконечно малую сферу.

4431.Жидкость, заполняющая пространство, вращается вокруг осиОz против часовой стрелки с постоянной угловой скоростью.Найти дивергенцию вектора скоростии вектора ускоренияв данной точке M(x, y, z) в данный момент времени.

4436. Найти: a) rot; б) rot .

4436.1.Найти величину и направление,если.

4438.Доказать, чтоdiv .

4439.Найти: a) rot (grad u); б) div (rot).

4441.Найти поток вектора:

a) через боковую поверхность конуса;

б) через основание этого конуса.

4442.Найти поток вектора:

а) через боковую поверхность цилиндра;

б) через полную поверхность этого цилиндра.

4444.Найти поток векторачерез положительный октант сферы ,.

4445.Найти поток векторачерез полнуюповерхностьпирамиды:.

4445.1.Найти поток векторачерез сферу.

27

4.

Демидович44 ( 52, 52.1, 52.2,54,55,57)

4452.Найти работу векторавдоль отрезка винтовой линии

.

4452. 1.Найти работу полявдоль прямолинейногоотрезка .

4452.2.Найти работу полявдоль прямолинейного отрезка ОМ: O(0, 0, 0), М(1, 3, 5).

4454.Найти циркуляцию вектора(с–постоянная): а)вдоль окружности(x– 2)² +y² = 1,z= 0;

б) вдоль окружностиx² +y² = 1,z= 0.

4455.Найти циркуляциюГвектора вдоль контураСв двух случаях: а)С–не окружает осьОz;

б) С–окружает осьОz.

4457.Показать, что поле

–потенциально и найти потенциал этого поля.

Батыгин,Топтыгин39а,б,в,г,д,е, 40 а,в,д, 42,43,

50(1,4), 51(1,2,3).

39а,б,в,г,д,е. Доказать тождества:

а)

б)

в)

г) ;

д) ;

е) .

28

40 а, в, д.Доказать тождества:

а)

б)

в)

42.Найти функциюудовлетворяющую условию:

43.Найти дивергенции и вихри следующих векторов:

гдеи–постоянные векторы.

50 (1).Вычислить, где-пост. вектор,-орт нормали к поверхности S.

50(4).Вычислить интегралгде–постоянный вектор,–единичный вектор нормали к поверхности S.

51 (1).Интеграл по замкнутой поверхности преобразовать в интеграл по объему, заключенному внутри поверхности(–орт нормали).

51 (2,3).Интегралы по замкнутой поверхностиS и(–постоянные векторы,–орт нормаликS)преобразовать в интегралы по объему, заключенному внутри поверхности.

*** Дополнение

Формула Грина: .

Формула Стокса:

; .

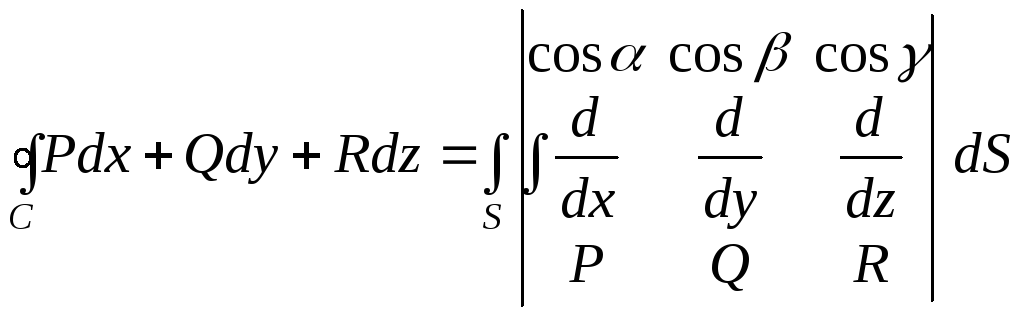29

Формула Гаусса – Остроградского:

;

.

Формула Ньютона – Лейбница: .

*

; .

Если z = z(x, y), то.

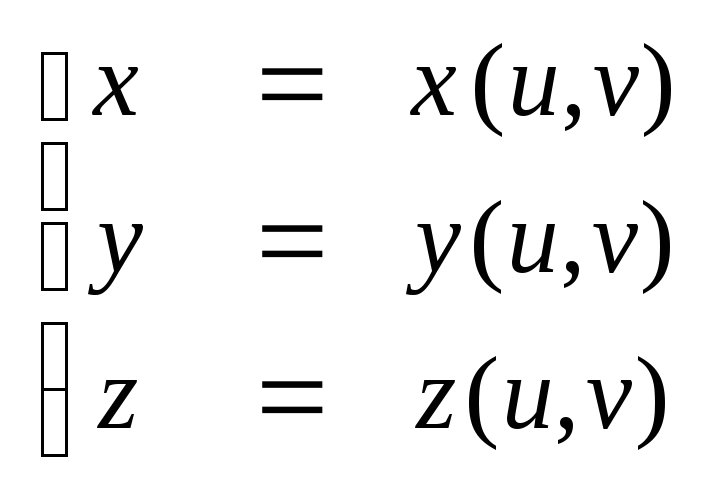Если т.е., то

; .

*