Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Лекции Соболева часть 3

.pdf

Скачиваний:

Добавлен:

23.02.2015

Размер:

3.38 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

18	Лекция 1 - 4

4.Тройной интеграл

Рассмотрим фигуру, которая является пространственной областью G . Интеграл по фигуре в данном случае является тройным интегралом от функции f (P) = f (x, y, z) по пространственной области G :

			n
∫ f (x, y, z)dµ = ∫∫∫ f (x, y, z)dV = limr →0 ∑ f (Pi				)∆Vi .
Φ	G	n	i=1
Φ	G		i=1

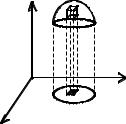
Область G будем называть правильной в направлении оси Oz , если:

1)любая прямая, параллельная оси Oz , пересекает границу области G не более чем в двух точках;

2)область G проектируется на координатную плоскость Oxy в правильную плоскую область D ;

3)любая часть области G удовлетворяет первым двум пунктам.

Примером таких областей является эллипсоид, куб, параллелепипед.

4.1. Задача о вычислении массы тела

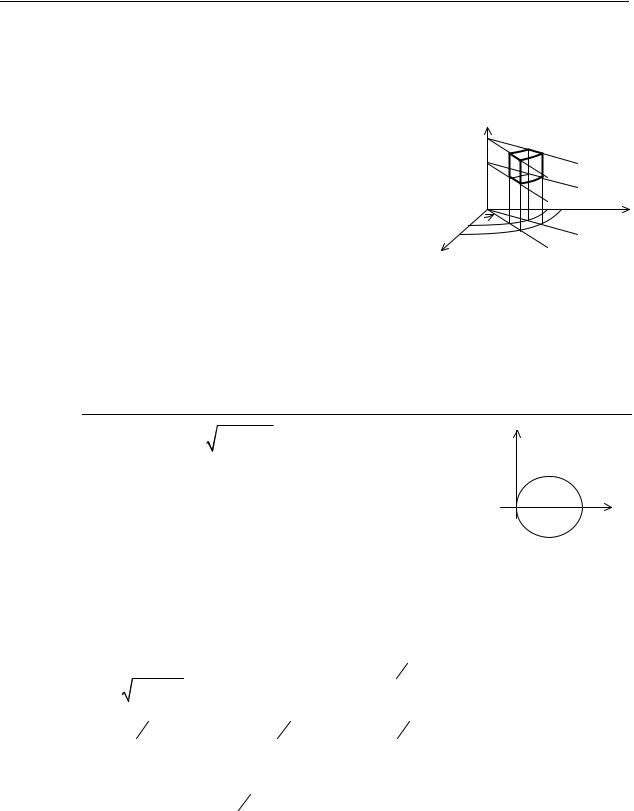
Пусть область V является правильной в направлении оси Oz , то есть ограничена снизу и сверху соответственно однозначными непрерывными поверхностями: z1 = z1(x, y) и

z2 = z2 (x, y) , причем проекцией области V на координатную плоскость Oxy является плоская область D , ограниченная линиями:

z		z2 ( x, y)
z	M 2
V			z1 ( x, y)

	M1
	M1
0	c y		d
0			y
a
x	M		D
b x			D
b x

y = y1 (x), y = y2 (x), x = a, x = b. M (x, y,0), M1(x, y, z1), M2 (x, y, z2 ) .

Отсюда следует, что при фиксированных значениях (x, y) D соответствую-

щие аппликаты		z точек области V		изменяются	в	пределах:
z1 (x, y) ≤ z ≤ z2 (x, y) .
Пусть тело V		материально, а объемная плотность ρ = ρ(P) = ρ(x, y, z) =
= f (x, y, z).	По	физическому	смыслу	интеграла	по	фигуре

m = ∫∫∫ρ(x, y, z)dV . Вычислим массу данного тела. Для этого рассечем тело

плоскостями, параллельными координатным плоскостям:

Кратные интегралы

x, x + ∆x y, y + ∆y . z, z + ∆z

Z2(x,y)

Этими плоскостями тело разбивается на паралле-	Z1(x,y)
	D
лепипеды, объем каждого из которых равняется	X
∆Vi = ∆xi ∆yi ∆zi . Выберем в пределах каждого
из них по точке Mi (xi , yi , zi ) .

Примем приближенно, что в пределах части ∆Vi плотность постоянна и

равна ρ(xi , yi , zi ) . Тогда масса части ∆Vi равна mi ≈ ρ(xi , yi , zi ) ∆Vi ,

mi ≈ ρ(xi , yi , zi ) ∆Si ∆zi , а масса всего тела равна m ≈ ∑ρ(xi , yi , zi )∆Vi . Если

i=1

диаметры всех элементарных частей стремятся к нулю, то в пределе это ра-

							n
венство становится точным и m = maxlimd →0 ∑ρ(xi , yi , zi )∆Vi , rn → 0 , ∆Vi → dV ,
						i	i=1
∆Si → dS . Вычислим массу столбика с основанием dS :
			z2	(x, y)
	mi = dS			∫	ρ(x, y, z)dz .
			z1(x, y)
Масса всего тела m =		lim		n
Масса всего тела m =		lim		∑mi∆Si ,
		max di →0		i=1
				i=1
		z2	(x, y)
следовательно, m = ∫∫dS			∫	ρ(x, y, z)dz .
	D	z1(x, y)
Таким образом ∫∫∫ f (x, y, z)dV = ∫∫dS						z2 (x, y)		(x, y, z)dz .
Таким образом ∫∫∫ f (x, y, z)dV = ∫∫dS						∫	ρ	(x, y, z)dz .
	G				D	z1(x, y)

!	Для вычисления ∫∫∫		необходимо вычислить интеграл по переменной z ,
	Для вычисления ∫∫∫		необходимо вычислить интеграл по переменной z ,
		G
	считая x и y фиксированными переменными, а затем вычислить ∫∫ по
проекции этого тела D на плоскость xOy :
					b	y2 (x)		z2 (x, y)
	∫∫∫ f (x, y, z)dV = ∫dx ∫						dy	∫	f (x, y, z)dz .
	G				a	y1(x)		z1(x, y)

20	Лекция 1 - 4
Таким образом, чтобы вычислить ∫∫∫	по правильной области G , необ-

ходимо вычислить трехкратный повторный интеграл.

1). dV = dxdydz называют дифференциальным элементом объема в де-

!картовой системе координат.

2). В повторных интегралах пределы интегрирования могут зависеть только от тех переменных, по которым еще не проведено интегрирование. Внешний интеграл всегда вычисляется в постоянных пределах.

3) Если область D задана неравенствами c ≤ y ≤ d , x1( y) ≤ x ≤ x2 ( y) , то

∫∫∫ f (x, y, z)dxdydz = ∫d dy		x ( y)	z		( x, y)
∫∫∫ f (x, y, z)dxdydz = ∫d dy		2∫	dx	2	∫ f (x, y, z)dz .
V	c	x1( y)	z1( x, y)

Пример:

z	C(0,0,1)
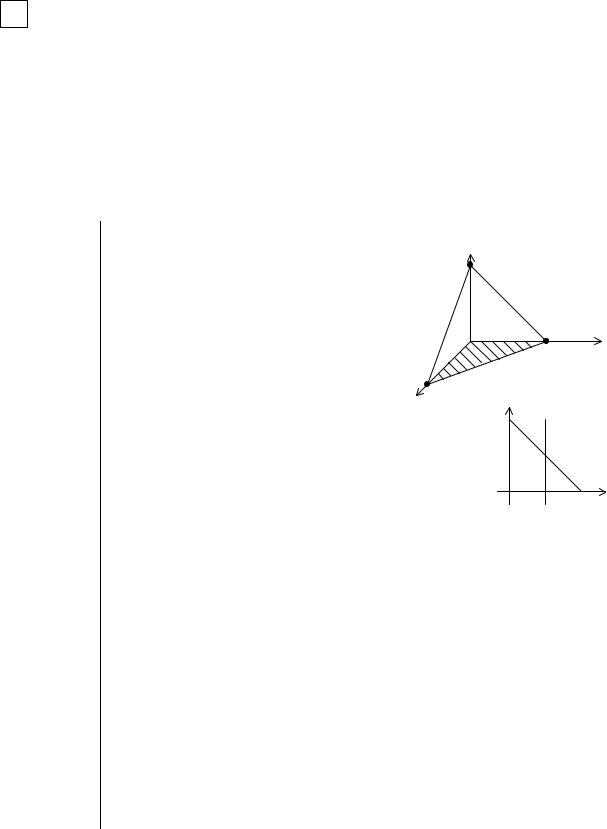
Вычислите ∫∫∫xyzdxdydz , где G - пи-
G	V
рамида, ограниченная плоскостями	V
x = 0 , y = 0 , z = 0 , x + y + z =1 .	0	B(0,1,0)
	0	y
Решение:	D	y
Решение:

Плоскость ABC : x + y + z =1 . Проекция	x	A(1,0,0)
области V на плоскость xOy есть		y
области V на плоскость xOy есть		(0,1)
∆OAB , ограниченный прямыми x = 0 ,		x + y =1
y = 0 , AB : x + y =1.		x + y =1
y = 0 , AB : x + y =1.

При (x, y) D аппликаты точек (x, y, z) V																																					0				(1,0)	x
удовлетворяют неравенству 0 ≤ z ≤1− x − y .																																					x [0,1], 0 ≤ y ≤1					− x
									1			−		1−x−y								1		−					2		1−x−y
												−		1−x−y										−							1−x−y
											1 x													1	x			z
∫∫∫xyzdxdydz = ∫xdx ∫													ydy		∫			zdz = ∫xdx ∫								ydy		z								=
∫∫∫xyzdxdydz = ∫xdx ∫													ydy		∫			zdz = ∫xdx ∫								ydy										=
G									0		0				0							0			0			2			0
	1		1		1−x								(1− x)y + y2 ]dy =
=	1		∫xdx ∫			y[(1− x)2 −2							(1− x)y + y2 ]dy =
	2		0		0
	1 1						2 y2								y3				y4 1−x							1 1									4		1		2		1
=			∫0	x (1− x)						−2(1− x)								+					dx =				x (1+ x)											−		+	dx =
=	2			x (1− x)					2	−2(1− x)					3			+	4				dx =				x (1+ x)										2	−	3	+	dx =
	2								2						3				4		0					2 ∫0											2		3		4
=		1		1 1 −		1 − x				1 − x			)	4 dx	=		1			1		1 − x		)	4 dx −			1		1		− x		)		5 dx			=
=				1 1 −		1 − x				1 − x				4 dx	=							1 − x			4 dx −			∫		1		− x				5 dx			=
	24			∫		(			) (						24					∫(								∫	(
	24			0											24					0								0
	1				(1 − x)5			x =1			(1		− x)6			x =1					1 1					1				1
	1				(1 − x)5			x =1			(1		− x)6			x =1					1 1					1				1
=				−						+									=					−			=						.
=	24			−		5				+				6					=					−		6	=	720					.
	24					5								6							24 5					6		720
									x =0							x =		0
									x =0							x =		0

Кратные интегралы

4.2.Замена переменных в тройном интеграле

Цель: упростить вычисление интеграла.

ТЕсли функции x = x(u,v,t), y = y(u,v,t), z = z(u,v,t) являются непрерывно дифференцируемыми и взаимно однозначно отображают точки пространства u,v,t на точки пространства x, y, z и наоборот и якобиан пе-

рехода, численно равный определителю третьего порядка, не равен нулю

	∂x	∂x	∂x
	∂x	∂x	∂x
	∂u	∂v	∂t
J =	∂y	∂y	∂y	, то при замене переменных в тройном интеграле
	∂u	∂v	∂t
	∂z	∂z	∂z
	∂u	∂v ∂t
справедлива формула ∫∫∫ f (x, y, z)dV = ∫∫∫ f (u,v,t )						J	dudvdt .


				G	G′		dV ′

Частным случаем преобразования координат является переход от декартовых координат к цилиндрическим и сферическим координатам.

4.3.Тройной интеграл в цилиндрических координатах

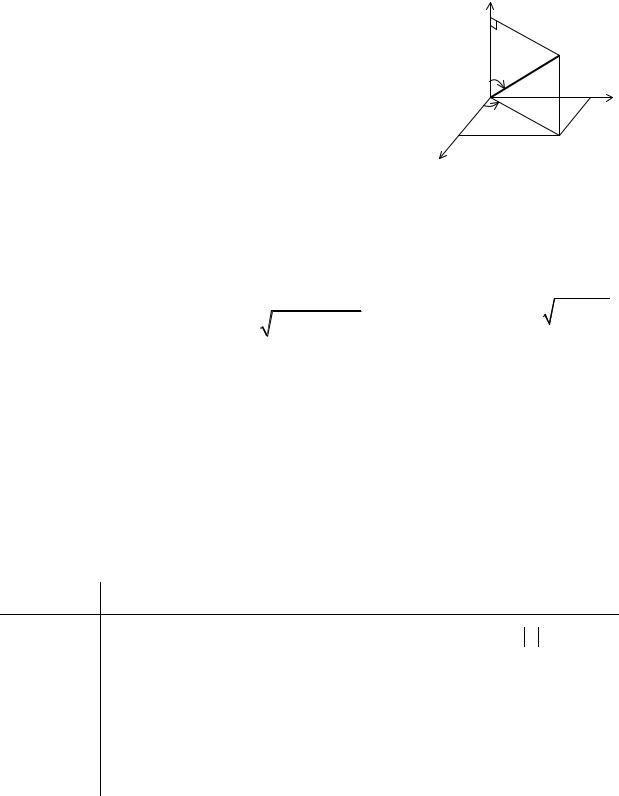
Цилиндрические координаты представляют собой соединение полярных координат в плоскости xOy с декартовой аппликатой z.

M ( ρ,ϕ , z )

x = ρcosϕ,	0	≤ ρ < ∞,
	0	≤ϕ < 2π,
y = ρsinϕ,
	−∞ < z <∞.
z = z,

Найдем якобиан перехода:

cosϕ −ρ sinϕ J (ρ,ϕ, z)= sinϕ ρ cosϕ

0 0

	0	y
	ϕ
x		ρ

0 = ρ cos2 ϕ + ρ sin2 ϕ = ρ ; 1

22 Лекция 1 - 4

∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (ρcosϕ, ρsinϕ, z)ρ d ρ dϕ dz .

V V ′

4.4. Элемент объема в цилиндрических координатах

Для вычисления элемента объема в цилинд-
рических координатах разобьем область V коор-
динатными поверхностями: ϕ = ϕi		-
полуплоскости, проходящие	через Oz, ρ = ρj	–
круговые цилиндры; z = zk –	плоскости, перпен-		x

∆z z

ϕ ρ	∆ρ	y
	∆ρ	∆ϕ
		∆ϕ

дикулярные оси Oz . Элементарным объемом будет криволинейная призма.

Площадь основания с точностью до бесконечно малых высшего порядка равна (ρ ∆ϕ) ∆ρ ; высота равна ∆z . Тогда

∆V ≈ ρ ∆ϕ ∆ρ ∆z , dV = ρ d ρ dϕ dz .

Пример:

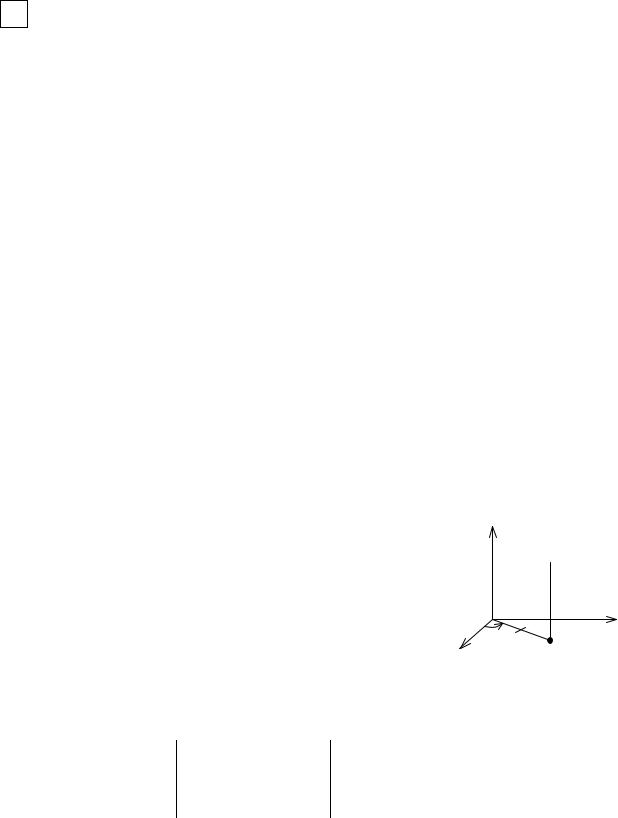
Вычислите ∫∫∫z

+ y

dx dy dz , где область V

ограничена цилиндром x2 + y2 = 2x и плоскостями

y ≥ 0, z = 0, z = a .

x( ρ)

Решение:

x2 + y2 −2x = (x −1)2 + y2 −1 = 0 ,

Уравнение

(x −1)2 + y2 =1 представляет собой окружность с R =1

и центром в точке

(1,0) . В полярных координатах ρ2 = 2ρ cosϕ .

Пределы изменения новых переменных: 0 ≤ z ≤ a , 0 ≤ϕ ≤

, 0 ≤ ρ ≤ 2cosϕ .

π 2

2 cosϕ

∫∫∫z

x2 + y2 dx dy dz = ∫∫∫z ρ ρ d ρ dϕ dz = ∫ dϕ

∫ ρ2d ρ∫zdz =

V ′

π 2

2cosϕ

π 2

= 12 a2 ∫ dϕ

∫ρ2 dρ =

a2 ∫cos3 ϕdϕ =

a2 ∫(1−sin 2 ϕ)d (sinϕ) =

sin3

π 2

sinϕ −

Кратные интегралы	23
4.5. Тройной интеграл в сферических координатах

Положение точки M (x, y, z) в пространстве						z
определяется	тремя	числами	θ, ρ, ϕ.			B
M (x, y, z)→ M (ρ,θ,ϕ).		Сферические координа-						M(ρ,θ,ϕ)
ты ρ, θ, ϕ : ρ	– радиус-вектор OM , θ		–	угол			θ	ρ
						0
между радиус-вектором и осью Oz , ϕ			–	угол				y
						ϕ

между проекцией ρ на плоскость xOy и осью Ox.					x			A
Сферические координаты связаны с декартовыми

следующими соотношениями:

ρ ≥ 0,0 ≤θ ≤π,

0 ≤ϕ ≤ 2π,

x = ρ sinθ cosϕ,y = ρ sinθ sinϕ,

z = ρ cosθ.

При этом x2 + y2 = ρ2 sin2 θ , ρ = x2 + y2 + z2 , ϕ = arctg	y	, θ = arctg	x2 + y2	.
	x
			z
Якобиан перехода:

J(ρ,ϕ,θ )=

∫∫∫f

sinθ cosϕ	−ρ sinθ sinϕ	ρ cosθ cosϕ	= ρ2 sinθ.
sinθ cosϕ	−ρ sinθ sinϕ	ρ cosθ cosϕ
sinθ sinϕ	ρ sinθ cosϕ	ρ cosθ sinϕ
cosθ	0	−ρ sinθ

(x, y, z)dxdydz = ∫∫∫ f (ρ,θ,ϕ)ρ2 sinθd ρdϕdθ .

V ′

Пример:

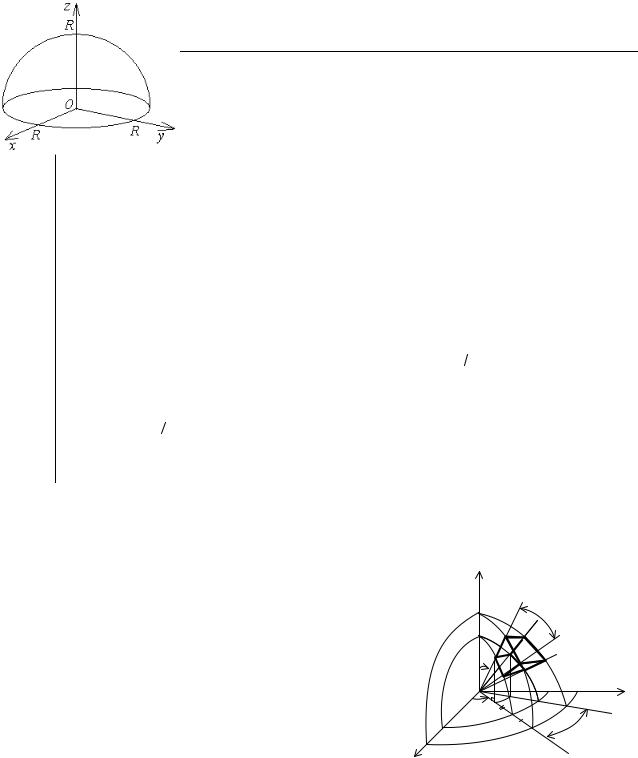
Найти объем шара радиуса R. Vшара = ∫∫∫dV = ∫∫∫dxdydz = ∫∫∫ J d ρdϕdθ =

V ′

=∫∫∫ρ2 sinθdρdϕdθ =π∫sinθdθ

2∫π dϕ∫R ρ2dρ =π∫sinθdθ

2∫π dϕ R3

V′

0 0

= π∫sinθdθ

2πR3

2πR3 π∫sinθdθ =

2πR3

(−cosθ )

π0 =

πR3.

24	Лекция 1 - 4

Пример:

Вычислите	∫∫∫(x 2 + y 2 )dxdydz ,	где	V - верхняя	поло-
	V
вина шара x 2 + y 2 + z 2 ≤ R2 .
Решение:
Введем сферические координаты. Новые
переменные	изменяются	в	пределах:

0 ≤ ρ ≤ R,0 ≤ ϕ ≤ 2π, 0 ≤θ ≤ π2 .

Тогда

x2 + y2 = ρ2 sin2 θ cos2 ϕ + ρ2 sin2 θ sin2 ϕ = ρ2 sin2 θ.

В результате

π 2

2π

∫∫∫(x2 + y2 )dxdydz = ∫∫∫ρ4 sin3 θd ρdθdϕ = ∫ρ4 d ρ ∫

sin3 θdθ ∫ dϕ =

V ′

π 2

= 2π ∫ρ4 d ρ ∫

(cos2 θ −1)d(cosθ ) = 2π ∫ρ4d ρ

cos3 θ −cosθ 2

π R5 .

4.6. Элемент объема в сферических координатах

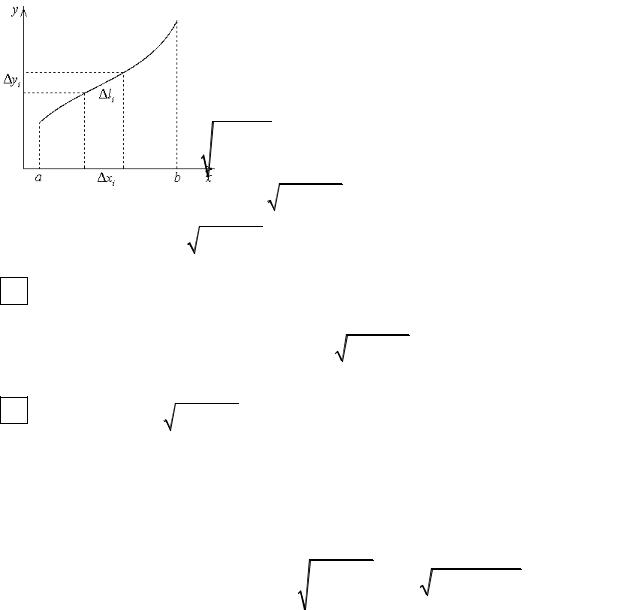
Вычислим элемент объема в сферических координатах. Разобьем область на элементарные части ∆V координатными поверхностями: ρ = ρi – сферы, θ =θj – кони-

ческие поверхности с вершиной в начале координат, ϕ =ϕk – полуплоскости, прохо-

дящие через ось Oz .

Здесь AB = ∆ρ ; из ∆OCC′: C′O =

= ρcos(900 −θ) = ρsinθ . Дуги AC = ρ∆θ ,

AD = CK = C′K′ = C′O ∆ϕ = ρsinθ ∆ϕ .

∆θ

∆z
z θ C	K B
	A
0	D	y
		y

ϕ C′ρ	K ′
	∆ρ	∆ϕ
		∆ϕ

С точностью до беконечно малых высшего порядка элементарный объем ∆V можно считать параллелепипедом с ребрами ∆ρ , ρ∆θ и ρsinθ ∆ϕ .

Элемент объема ∆V ≈ ρ2∆ρsinθ∆θ∆ϕ , dV = ρ2d ρsinθ dθ dϕ .

Кратные интегралы

5. Криволинейные интегралы первого типа (рода)

Рассмотрим фигуру, которая является плоской либо пространственной кривой Ф→L. Интеграл по фигуре в данном случае является криволинейным интегралом первого рода от функции f (P) по кривой L:

∫ f (P)dl = lim ∑ f (Pi )∆li , Pi L .

rn →0 i=1

5.1. Способы вычисления криволинейного интеграла первого типа

5.1.1. Криволинейный интеграл первого типа по плоской кривой

Пусть

плоская

кривая

задана уравнением

L : y =ϕ(x).

Выберем бесконечно малый участок ∆xi на

отрезке a ≤ x ≤ b . Тогда ∆l 2 ≈ ∆x 2

+∆y 2 ,

∆l

≈ (1 +

∆y 2

)∆x

∆l ≈ 1 +

∆y

∆x . Переходя к

∆x 2

пределу при ∆xi → 0 , имеем dl =

1 + ( y′x )2 dx ,

∫ f (x, y)dl = ∫b

f (x,ϕ(x)) 1 + ( y′x )2 dx .

!Чтобы вычислить криволинейный интеграл первого типа по плоской кривой, необходимо переменную y заменить на выражение y =ϕ(x) (из

уравнения линии), а dl заменить на 1 + ( y′x )2 dx и вычислить определенный интеграл по x.

!Величина dl = 1 + ( y′x )2 dx называется дифференциальным элементом длины плоской кривой.

x = x(t)	α ≤ t ≤ β , то
Если линия задана в параметрическом виде: L :	α ≤ t ≤ β , то
y = y(t)

y′

′

dx =

′ , dl =

1 + (

)

dt ;

yx =

′) xt dt =

(xt )

+ ( yt

26 Лекция 1 - 4

∫ f (x, y)dl = ∫ f (x(t), y(t)) (xt′)2 + ( yt′)2 dt .

L α

5.1.2. Криволинейный интеграл первого типа по пространственной кривой

x = x(t)

L : y = y(t) α ≤ t ≤ β , dl = (xt′)2 + ( yt′)2 + (zt′)2 dt;

z = z(t)

∫ f (x, y, z)dl = ∫ f (x(t), y(t), z(t)) (xt′)2 + ( yt′)2 + (zt′)2 dt .

L α

Пример:

Найти массу полуокружности, заданную уравнениями:

	2	+ y	2	=1, Линейная плотность
L : x		+ y		=1, Линейная плотность
y ≥ 0.

ρ(x, y) = ky.

Уравнение полуокружности в параметри-

x = cost,

L : y = sint,

ческом виде имеет вид

o ≤ t ≤π.

m = ∫ρ(x, y)dl = ∫kydl = k		π∫sin t	sin2 t +cos2 tdt = kπ∫sin tdt =
L	L	o	o

=k(−cos t)πo = k(1+1) = 2k .

5.2.Геометрический смысл криволинейного интеграла первого типа по плоской кривой

Пусть на плоскости xOy задана кривая L. На множестве L определена функция z = f (P) = f (x, y) . Разобьем кривую L на n частейLi длиной ∆li . Выберем на кривой L точку Pi , вычислим значение функции z = f (Pi ) = f (xi , yi ). Тогда площадь прямоугольного участка равна ∆Si = f (xi , yi )∆li .

Кратные интегралы		27
n
Найдем сумму площадей ∑f (xi , yi )∆li .
i=1
Перейдем к пределу при n → ∞, тогда
	n
S = limn→∞	∑ f (xi , yi )∆li = ∫ f ( p)dl .
	i=1	L

Таким образом, криволинейный интеграл первого типа по плоской кривой численно равен площади боковой поверхности цилиндра с направляющей L и образующей, длина которой z = f (P) = f (x, y) .

6. Механические приложения интегралов по фигуре

6.1. Длина, площадь, объем фигуры

Длина участка кривой равна l =∫dx, площадь плоской фигуры равна

S = ∫∫dxdy , объем тела V = ∫∫∫dxdydz .

D V

6.2. Масса фигуры

Масса неоднородного тела с плотностью ρ(x, y, z) :

m = ∫∫∫ρ(x, y, z)dxdydz .

Пример:

	Найдите массу тела, ограниченного цилиндрической поверхностью x2					= 2 y
	и плоскостями y + z =1, 2 y + z = 2 ,	если	в каждой	его точке плотность
	ρ(x, y, z) = y .
	Решение:
	Из y + z =1 получаем, что при z = 0	y =1, а при y = 0		z =1; из 2 y + z = 2
	получаем, что при z = 0 y =1, а при y = 0
	z = 2 .		z		2y + z = 2
	Линии пересечения плоскостей с		2		2y + z = 2
	Линии пересечения плоскостей с		2
	координатной плоскостью zOy : z =1− y и				y + z =1
	z = 2(1− y) .		1	V	y + z =1
	z = 2(1− y) .		1	V
	В плоскости xOy направляющей цилинд-					B
	рической поверхности является парабола		0		1	y
	x2 = 2 y .				D A
	Проекция тела на плоскость xOy D огра-				x2 = 2 y
	Проекция тела на плоскость xOy D огра-		x		y =1
	ничена линиями: y =1, 0 ≤ y ≤1;

<<< < Предыдущая 1 23 / 143 4 5 6 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
10.11.2019861.18 Кб53Лекции РИМ сводная_1.doc
#
17.11.2019235.52 Кб5Лекции РЦБ - кусочки.doc
#
21.12.2018681.98 Кб40Лекции сенсоры.doc
#
24.08.2019642.56 Кб28Лекции сенсоры.doc
#
23.02.2015732.41 Кб12лекции сист эл снабж.pdf
#
23.02.20153.38 Mб58Лекции Соболева часть 3.pdf
#
22.02.20151.15 Mб282Лекции соц психология.doc
#
23.02.20154.81 Mб90Лекции Стечкина по матану.pdf
#
21.12.201816.1 Mб40Лекции ТЭПП.doc
#
31.08.2019196.83 Кб7Лекции Философия.docx
#
20.09.20191.05 Mб13лекции ЦБ.docx